Многомерные системы регулирования

К многомерным относятся системы управления и регулирования, имеющие несколько регулируемых величин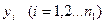

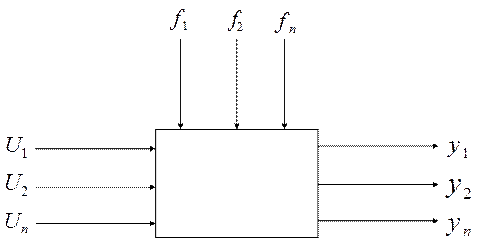
Многомерная система предполагает наличие многомерного объекта управления, который характеризуется существованием нескольких входов (точек приложения управляющих и возмущающихвоздействий) и нескольких выходов, определяющих результируемыми величинами.

 

В общем случае переменные и возмущения связаны между собой и с параметрами устройств, вырабатывающих , …системой дифференциальных урпавнений, которые принято записывать в форме Коши.

Пример: требуется следить за дальностью D до цели и скоростью сближения 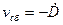измерителя с целью.

Если измеритель неподвижен, а цель перемещается с постоянным ускорением , направленным вдоль РСН, относительно движение цели и измерителя характеризуется тремя дифференциальными уравнениями в форме Коши:

Многомерный объект описывается системой уравнений, которую удобно представить в векторно-матричной форме (без обозначения зависимости от t)

Здесь

- вектор управляемых параметров, с компонентами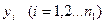

- динамическая матрица 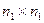, элементы которой отображают динамические свойства устройств формирования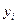

вектор управления, содержащий состав

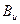- матрица управления размером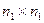

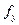- вектор возмущающих воздействий

Структурная схема замкнутой многомерной системы регулирования

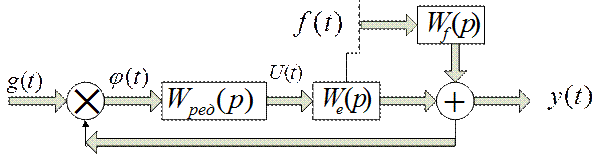
Все символы соответствуют матрицам:

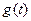- задающих воздействий

- регулируемых величин

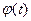- ошибок для каждой регулируемой величины

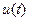- управляющих воздействий

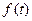- возмущений

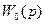- передаточных функций для управления

- передаточных функций для возмущения

 

- передаточных функций для регулирующего устройства, которое определяет используемые законы управления

Исходные дифференциальные уравнения ортогональной системы могут быть представлены в форме Коши в векторной (матричной) записи

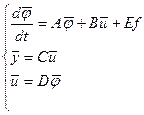
Когда описывается внутренняя структура системы – в описание в пространстве состояний, кроме «внешних» переменных g и y, вводятся «внутренние» переменные (переменные состояния) …

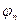
Число переменных состояния равно размерности системы и, как правило, совпадает с порядком передаточной функции

Стандартное описание:

,

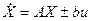Что эквивалентно:

 

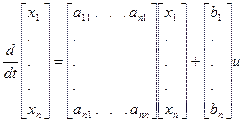
Постоянная (квадратная) матрица А характеризует внутреннюю структуру системы и ее свободное движение

Постоянные матрицы В и С характеризуют структуру входного и выходного устройств.

 

Может быть приведено к каноническому виду после соответствующего выбора переменных состояния (линейно-независимых). Их число всегда должно быть равно порядку объекта – порядку д.у.

Проще всего в качестве переменных состояния брать у и ее производные до (n-1)-й включительно.

, . . .

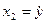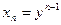
Следовательно, имеем систему уравнений:

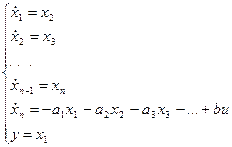
Равносильно:

-

 

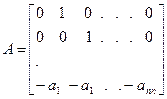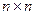
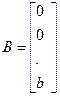
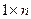
Одноканальный объект

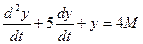
Выбираем переменные состояния

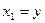
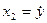
Следовательно, уравнения состояния и матрицы объекта:

 

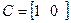
2.

Переменные состояния:

 

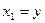
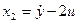
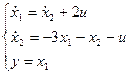
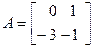
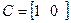
Можно по матричному описанию найти передаточную функцию

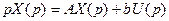
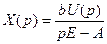
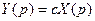
Следовательно:

 

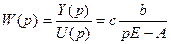
Т.е. знаменатель ПФ совпадает с характеристическим полиномом матрицы А