Дифференциальное уравнение линейной САУ и ее передаточная функция

 

Основной характеристикой любой динамической системы, наиболее полно отражающей ее свойства, является дифференциальное уравнение.

Процессы, описывающие линейную САУ, соответственно, будут описываться линейным дифференциальным уравнением.

Общий метод составления дифференциального уравнения системы: для каждого звена автоматической системы в соответствии с его теорией составляют дифф.ур. связывающее его выходную величину с входной. В результате получают систему уравнений, количество которых равно числу звеньев. Входные и выходные величины – основные, остальные промежуточные, которые из системы исключаются при ее решении.

Общий вид такого уравнения:

(2.1)

 

Где:

y – управляемая (выходная) величина САУ

g – задающая (входная) величина САУ

Дифференциальное уравнение связывает управляемую величину САУ y(t) с задающим воздействием g(t)

В САУ традиционно выполняется соотношение n > m – это закон ее функционирования.

Так как все функции и их производные стоят в первой степени, для такого дифференциального уравнения выполняется принцип суперпозиции, следовательно, такая система линейна.

Дифференциальные уравнения сложны, для упрощения описания САУ и анализа их функционирования применяется преобразование Лапласа. Делаем мы это, чтобы получить передаточную функцию САУ

Передаточная функция системы – это отношение изображения по Лапласу выходной управляемой величины к изображению по Лапласу задающего воздействия.

Где:

Есть таблица готовых преобразований Лапласа

 

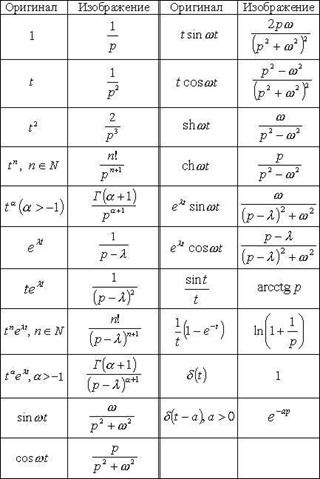
Как известно:

Для получения передаточной функции САУ найдем преобразование Лапласа от обеих частей уравнения (2.1)

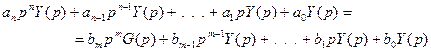
Т.о. уравнение дифференциальное преобразовано в уравнение алгебраическое.

Передаточная функция, следовательно, имеет вид:

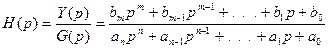
Передаточная функция является основной характеристикой САУ

Сразу описать систему в целом сложно, но передаточная функция может определиться для функции в целом, если мы узнаем передаточную функцию каждого из звеньев.

Известная ПФ позволяет получить временные и частотные характеристики САУ

Пример:

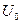- источник питания, подаваемого на перестраиваемые резисторы

- напряжение на резисторе

- напряжение на резисторе

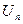- напряжение на резисторе

Разница напряжений между резисторами

- напряжение, подаваемое на обмотку возбуждения двигателя обеспечения его работы

Дискриминатор в данном случае построен на , и источнике питания

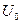
Задающее воздействие 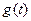определяет величину и соответственно

Положение оси двигателя – управляемая величина - определяет и соответственно

Т.о. в дискриминаторе сравнивается угловое положение осей и находится ошибка.

В системе используется два вида связи, две линии – электрическая и механическая.

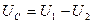, причем

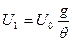
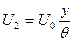
- угол поворота ручек потенциометра

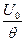- коэффициент передачи

- ошибка

Равенства угла поворота исполнительной оси и угла поворота командной оси 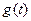. В этом случае ошибка равна 0 и напряжение на входе усилителя и на его выходе тоже будет нулевым, т.е. двигатель неподвижен.

Определим зависимость между ошибкой 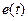и положение исполнительной оси

1. Уравнение дискриминатора
2. Уравнение усилителя
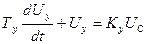
3. Уравнение двигателя
4. Редуктор

Определим, исходя из (1) – (4), связь между управляемой величиной и задающим воздействием с учетом преобразования Лапласа.

1. 
2. 
3. 
4. 

Следовательно, передаточная функция

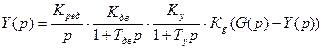
Обозначим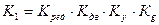

Тогда:

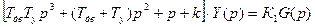
Следовательно

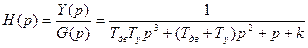
Дифференциальное уравнение: