рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Базовые понятия теории и методические рекомендации по решению задач
Реферат Курсовая Конспект
Базовые понятия теории и методические рекомендации по решению задач
Базовые понятия теории и методические рекомендации по решению задач - раздел Философия, МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ Для студентов всех форм обучения по направлениям 151000.62 «Технологические машины и оборудование» 190600.62 «Эксплуатация транспортно-технологических машин и комплексов» Сложным Движением Называют Такое Движение, При Котором Точка Одновреме...
Сложным движением называют такое движение, при котором точка одновременно участвует в двух или более движениях. Абсолютным движением называют движение точки М по отношению к основной системе отсчета 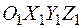 , которую условно принимают за неподвижную. Относительным движением называют движение точки М по отношению к подвижной системе отсчета OXYZ. Переносным движением называют движение подвижной системы отсчета OXYZ относительно основной (неподвижной) системы отсчета
, которую условно принимают за неподвижную. Относительным движением называют движение точки М по отношению к подвижной системе отсчета OXYZ. Переносным движением называют движение подвижной системы отсчета OXYZ относительно основной (неподвижной) системы отсчета 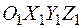 .
.
Абсолютной скоростью называют скорость точки М относительно основной системы координат 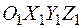 и обозначают
и обозначают  .
.
Относительной скоростью называют скорость точки М относительно подвижной системы координат OXYZ и обозначают  .
.
Переносной скоростью называют скорость той точки подвижной системы координат, с которой в данный момент совпадает движущаяся точка М, и обозначают 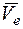 .
.
Абсолютная скорость точки в сложном движении равна геометрической сумме переносной и относительной скоростей
 .
.
Модуль абсолютной скорости в общем случае находят проецированием на оси координат, так как угол между векторами относительной и переносной скоростей может быть от 0 до 180°:
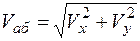 ,
,
где
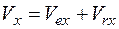 ,
,
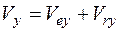 .
.
Определение скоростей относительного и переносного движений начинают с нахождения положения точки на траектории относительного движения. Затем мысленно останавливают относительное движение и определяют скорость той точки подвижной системы координат, в которой зафиксирована движущаяся точка. Это будет переносная скорость. Для определения относительной скорости мысленно останавливают движение подвижной системы координат, т. е. переносное движение, и известными способами находят скорость точки относительно подвижной системы координат.
Абсолютное ускорение точки в сложном движении равно геометрической сумме переносного, относительного и кориолисова ускорений:
 ,
,
где  — ускорение переносного движения;
— ускорение переносного движения; 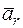 — ускорение относительного движения;
— ускорение относительного движения; 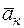 — ускорение Кориолиса:
— ускорение Кориолиса:
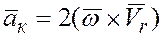 .
.
Ускорение Кориолиса характеризует:
1. Изменение величины переносной скорости точки вследствие ее относительного движения.
2. Изменение направления вектора относительной скорости вследствие вращательного переносного движения.
Направление ускорения Кориолиса определяют либо по правилу векторного произведения, либо по правилу Жуковского.
Правило векторного произведения: ускорение Кориолиса направлено перпендикулярно плоскости векторов 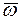 и
и  в ту сторону, откуда виден поворот от
в ту сторону, откуда виден поворот от 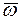 к
к  на наименьший угол против хода часовой стрелки.
на наименьший угол против хода часовой стрелки.
Поворот вектора 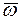 к вектору
к вектору  против хода часовой стрелки на наименьший угол виден со стороны отрицательных значении оси X, куда и направлен вектор ускорения Кориолиса
против хода часовой стрелки на наименьший угол виден со стороны отрицательных значении оси X, куда и направлен вектор ускорения Кориолиса
( ).
).
Правило Жуковского: проецируем вектор относительной скорости  на плоскость, перпендикулярную вектору переносной угловой скорости, и поворачиваем эту проекцию в той же плоскости на угол 90° в сторону переносной угловой скорости.
на плоскость, перпендикулярную вектору переносной угловой скорости, и поворачиваем эту проекцию в той же плоскости на угол 90° в сторону переносной угловой скорости.
Проекция вектора относительной скорости на плоскость П, перпендикулярную вектору угловой скорости 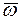 , равна
, равна  . Проекцию поворачиваем против хода часовой стрелки на 90° в соответствии с направлением переносной угловой скорости. Вектор ускорения Кориолиса будет направлен в сторону отрицательных значений оси X.
. Проекцию поворачиваем против хода часовой стрелки на 90° в соответствии с направлением переносной угловой скорости. Вектор ускорения Кориолиса будет направлен в сторону отрицательных значений оси X.
Равенство нулю ускорения Кориолиса возможно:
1. 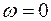 ; переносное движение является поступательным.
; переносное движение является поступательным.
2. 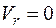 относительная скорость в данный момент равна нулю.
относительная скорость в данный момент равна нулю.
3.  ; вектор угловой скорости переносного движения со параллелен вектору относительной скорости
; вектор угловой скорости переносного движения со параллелен вектору относительной скорости  .
.
При вращательном переносном и криволинейным относительным движениях:
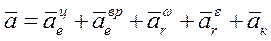 .
.
Модуль абсолютного ускорения
 .
.
При поступательном переносном и криволинейном относительном движениях :
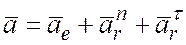 .
.
– Конец работы –
Эта тема принадлежит разделу:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ Для студентов всех форм обучения по направлениям 151000.62 «Технологические машины и оборудование» 190600.62 «Эксплуатация транспортно-технологических машин и комплексов»
САНКТ ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ... УНИВЕРСИТЕТ СЕРВИСА И ЭКОНОМИКИ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Базовые понятия теории и методические рекомендации по решению задач
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов