рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Рекомендации по решению задач
Реферат Курсовая Конспект
Рекомендации по решению задач
Рекомендации по решению задач - раздел Философия, МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ Для студентов всех форм обучения по направлениям 151000.62 «Технологические машины и оборудование» 190600.62 «Эксплуатация транспортно-технологических машин и комплексов» Момент Силы ...
Момент силы 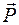 относительно точки О изображается вектором
относительно точки О изображается вектором  ,приложенным в этой точке и направленным перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы, смотря навстречу этому вектору, видеть силу
,приложенным в этой точке и направленным перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы, смотря навстречу этому вектору, видеть силу 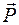 стремящейся вращать эту плоскость в сторону, обратную вращению часовой стрелки (рис. 4.1).
стремящейся вращать эту плоскость в сторону, обратную вращению часовой стрелки (рис. 4.1).
Если из точки О в точку приложения силы А провести радиус-вектор  , то вектор момента силы можно выразить следующим векторным произведением:
, то вектор момента силы можно выразить следующим векторным произведением:
 .
.

Рис. 4.1
Модуль этого вектора  равен произведению модуля силы Р на ее плечо d относительно точки О
равен произведению модуля силы Р на ее плечо d относительно точки О
 .
.
Моментом силы 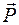 относительно оси z называется взятое со знаком плюс или минус произведение модуля проекции
относительно оси z называется взятое со знаком плюс или минус произведение модуля проекции  силы
силы 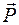 на плоскость, перпендикулярную оси, на ее плечо
на плоскость, перпендикулярную оси, на ее плечо  относительно точки О пересечения оси с плоскостью (рис. 4.2)
относительно точки О пересечения оси с плоскостью (рис. 4.2)
 .
.

Рис. 4.2
Момент силы относительно оси считается положительным, если смотря навстречу оси z, можно видеть проекцию  стремящейся вращать плоскость I вокруг оси z в сторону, противоположную вращению часовой стрелки. Момент силы относительно оси изображается отрезком, отложенным по оси z от точки О в положительном направлении, если
стремящейся вращать плоскость I вокруг оси z в сторону, противоположную вращению часовой стрелки. Момент силы относительно оси изображается отрезком, отложенным по оси z от точки О в положительном направлении, если 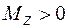 , и в отрицательном - если
, и в отрицательном - если  .
.
Момент силы относительно оси равен нулю в двух случаях:
1. Сила параллельна оси.
2. Линия действия силы пересекает ось.
Моменты силы относительно осей равны
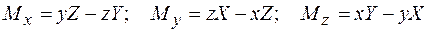 ,
,
где x,у,z – координаты точки приложения силы 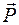 ; Х,Y,Z - проекции силы
; Х,Y,Z - проекции силы 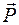 на координатные оси.
на координатные оси.
Пространственную систему сил можно привести к центру по аналогии с плоской системой. В результате приведения получается главный вектор и главный момент. В отличие от плоской системы сил главный момент в этом случае является векторной величиной.
Для равновесия пространственной системы сил необходимо и достаточно равенства нулю главного вектора и главного момента.
В координатной форме эти условия могут быть представлены в виде:
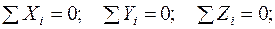
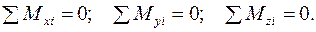
Заметим, что это всего лишь один из вариантов условий равновесия. Оси, на которые проецируются силы, могут и не совпадать с осями, относительно которых вычисляются моменты сил. Уравнения проекций можно заменить уравнениями моментов. Можно, например, составлять шесть уравнений моментов, а уравнения проекций не составлять. Единственное требование, предъявляемое к составленным уравнениям равновесия, состоит в следующем: все уравнения равновесия должны быть линейно независимы.
Следует отметить, что для составления уравнений более удобны уравнения проекций, а для решения - уравнения моментов. Задачи рекомендуется решать в следующей последовательности:
1. Действие каждой из опор заменяем двумя взаимно перпендикулярными реакциями, лежащими в плоскости, перпендикулярной валу.
2. Для определения силы давления составляем уравнение моментов относительно оси вала. Момент силы натяжения ремня, нити и т.п. (наклонной или нет) вычисляем как произведение величины силы на соответствующий радиус со знаком, соответствующим направлению вращения вокруг вала. Уравнение содержит одну неизвестную, которую легко найти.
3. Определяем вертикальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия горизонтальных реакций шарниров. Решаем эти уравнения.
4. Проверяем найденные реакции, составляя уравнение равновесия в проекции на вертикаль.
5. Определяем горизонтальные реакции опор вала. Для этого составляем два уравнения моментов относительно осей, совпадающих с линиями действия вертикальных реакций шарниров.
6. Проверяем горизонтальные реакции, составляя уравнение равновесия в проекции на ось вдоль линии действия горизонтальных реакций.
– Конец работы –
Эта тема принадлежит разделу:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ Для студентов всех форм обучения по направлениям 151000.62 «Технологические машины и оборудование» 190600.62 «Эксплуатация транспортно-технологических машин и комплексов»
САНКТ ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ... УНИВЕРСИТЕТ СЕРВИСА И ЭКОНОМИКИ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Рекомендации по решению задач
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов