рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Одномерные колебания однородной струны
Реферат Курсовая Конспект
Одномерные колебания однородной струны
Одномерные колебания однородной струны - раздел Механика, Колебания в кристаллах Рассмотрим Распространение Продольных Волн В Однородной Неограниченной Струне...
Рассмотрим распространение продольных волн в однородной неограниченной струне с плотностью ρ. Движение каждого из элементов струны происходит лишь в направлении ее длины.
Выделим бесконечно малый элемент струны толщиной 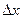 (рис.6.1).
(рис.6.1). 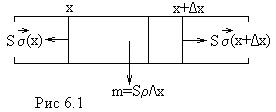 При распространении продольной волны на этот элемент действуют упругие силы: слева
При распространении продольной волны на этот элемент действуют упругие силы: слева 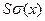 , справа
, справа 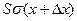 , где
, где 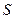 - площадь поперечного сечения струны, σ – нормальное упругое напряжение. Результирующая этих сил
- площадь поперечного сечения струны, σ – нормальное упругое напряжение. Результирующая этих сил 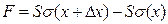 . Под действием силы F элемент
. Под действием силы F элемент 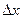 испытывает смещение. Обозначив u(x, t) смещение центра масс элемента
испытывает смещение. Обозначив u(x, t) смещение центра масс элемента 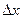 , запишем по второму закону Ньютона уравнение его движения:
, запишем по второму закону Ньютона уравнение его движения:
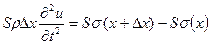 .
.
Здесь 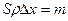 - масса элемента
- масса элемента 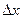 ,
,  - его ускорение. Разделив на S, имеем:
- его ускорение. Разделив на S, имеем:
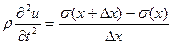 .
.
При x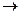 0 получаем
0 получаем 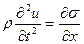 . Согласно закону Гука
. Согласно закону Гука 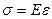 , где Е - модуль упругости (модуль Юнга);
, где Е - модуль упругости (модуль Юнга); 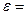
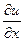 - деформация в точке, тогда
- деформация в точке, тогда
 .
.
Для смещения получаем уравнение
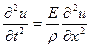 . (6.1)
. (6.1)
Это обычное волновое уравнение для упругих волн, распространяющихся вдоль струны. Решение этого уравнения будем искать в виде бегущей продольной монохроматической волны: 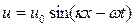 , где
, где 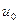 - амплитуда колебаний; t-время,
- амплитуда колебаний; t-время, 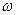 -круговая частота,
-круговая частота, 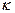 -волновое число.
-волновое число.
Подставив это решение в (6.1), получим:
 -
-
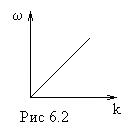 - для упругой волны, распространяющейся в неограниченно протяженной струне, частота колебаний линейно зависит от волнового числа (рис.6.2). При этом скорость распространения волны
- для упругой волны, распространяющейся в неограниченно протяженной струне, частота колебаний линейно зависит от волнового числа (рис.6.2). При этом скорость распространения волны 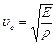 для данного материала величина постоянная, т.к. Е и ρ зависят только от материала. Так для железной струны
для данного материала величина постоянная, т.к. Е и ρ зависят только от материала. Так для железной струны 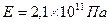 ,
, 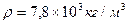 ,
, 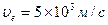 .
.
6.2.Упругие волны в монокристаллах
 Процессы распространения упругих волн в кристаллах много сложнее процессов распространения электромагнитных волн. Электромагнитные волны всегда поперечные, упругие (звуковые) волны могут быть как поперечными, так и продольными. Продольные волны - это волны сжатий и растяжений, поперечные - волны деформаций сдвига. В каждом заданном направлении в кристалле распространяются в общем случае три поляризованные упругие волны с разными скоростями.
Процессы распространения упругих волн в кристаллах много сложнее процессов распространения электромагнитных волн. Электромагнитные волны всегда поперечные, упругие (звуковые) волны могут быть как поперечными, так и продольными. Продольные волны - это волны сжатий и растяжений, поперечные - волны деформаций сдвига. В каждом заданном направлении в кристалле распространяются в общем случае три поляризованные упругие волны с разными скоростями.
Рассмотрим распространение упругих волн в кристалле, плотность которого ρ. Внутри кристалла выберем элементарный параллелепипед с ребрами 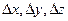 , параллельными кристаллографическим осям координат x,y,z (рис.6.3).
, параллельными кристаллографическим осям координат x,y,z (рис.6.3).
При движении упругой волны по кристаллу каждая грань элементарного параллелепипеда под действием напряжения  совершает небольшие перемещения. Для поступательного перемещения элементарного параллелепипеда при распространении упругой волны вдоль направления х имеем следующее: на грань х действует напряжение
совершает небольшие перемещения. Для поступательного перемещения элементарного параллелепипеда при распространении упругой волны вдоль направления х имеем следующее: на грань х действует напряжение 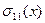 , на параллельную ей грань
, на параллельную ей грань  - напряжение
- напряжение 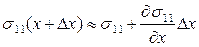 . Результирующая сила, действующая в направлении х, равна:
. Результирующая сила, действующая в направлении х, равна: 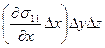 . Другие силы, действующие в направлении х , вызваны изменением внутри параллелепипеда напряжений
. Другие силы, действующие в направлении х , вызваны изменением внутри параллелепипеда напряжений  и
и  , так что в направлении х результирующая сила равна
, так что в направлении х результирующая сила равна
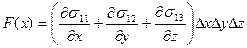 .
.
Пусть 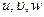 -компоненты вектора смещения центра масс параллелепипеда. Уравнение движения параллелепипеда в направлении х под действием напряжений имеет вид:
-компоненты вектора смещения центра масс параллелепипеда. Уравнение движения параллелепипеда в направлении х под действием напряжений имеет вид:
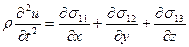 .
.
Оно имеет три решения.
Первое решение 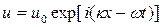 , оно описывает продольную волну, скоскорость распространения которой в направлении [100] (т.е. в направлении оси х) равна
, оно описывает продольную волну, скоскорость распространения которой в направлении [100] (т.е. в направлении оси х) равна 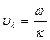 .
.
Второе решение описывает поперечную волну (волна сдвига), волновой вектор которой направлен вдоль ребра куба и совпадает с направлением х, эта волна дает смещение υ по направлению оси y: 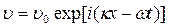 , скорость распространения ее в направлении [100]
, скорость распространения ее в направлении [100]
 ,
,
где cy - упругая постоянная поперечной волны в направлении [100].
Третье решение - это волна сдвига, волновой вектор которой направлен по оси х, смещение w происходит вдоль оси z:
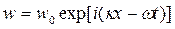 ,
,
скорость распространения ее в направлении [100] 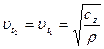 , где cz-упругая постоянная.
, где cz-упругая постоянная.
Таким образом, для одного и того же волнового вектора 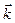 , параллельного направлению [100], возникают три упругие волны - одна продольная и две поперечные. При этом две независимые волны сдвига имеют одинаковые скорости. В случае произвольного вектора
, параллельного направлению [100], возникают три упругие волны - одна продольная и две поперечные. При этом две независимые волны сдвига имеют одинаковые скорости. В случае произвольного вектора 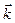 имеют место три поляризованные волны, распространяющиеся с разными скоростями, которые не зависят от частоты колебаний. При этом , чем меньше плотность и чем меньше жесткость кристалла, тем выше скорости распространения упругих волн. Круговая частота ω~
имеют место три поляризованные волны, распространяющиеся с разными скоростями, которые не зависят от частоты колебаний. При этом , чем меньше плотность и чем меньше жесткость кристалла, тем выше скорости распространения упругих волн. Круговая частота ω~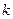 , т.е. результат тот же, что и для упругой струны.
, т.е. результат тот же, что и для упругой струны.
– Конец работы –
Эта тема принадлежит разделу:
Колебания в кристаллах
Тепловые свойства твердых тел Колебания в кристаллах Одномерные...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Одномерные колебания однородной струны
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов