Колебания атомов трехмерной решетки

Допустим, что трехмерная решетка состоит из одинаковых атомов массы M и на объем кристалла V приходится N элементарных примитивных ячеек Бравэ. Каждый атом имеет три степени свободы, поэтому весь кристалл имеет 3N степеней свободы. Колебания трехмерной кристаллической решетки описываются системой 3N связных уравнений движения, решения которых:

,

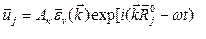где - вектор смещения j-ого атома, 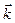- волновой вектор, определяющий направление распространения волны, А_к - амплитуда колебаний, - единичный вектор поляризации нормальной моды, описывающий направление, в котором движутся ионы, -радиус-вектор j-ого атома в равновесной конфигурации.

Решение уравнения движения показало, что для каждого волнового вектора 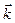имеют место три моды колебаний (рис.8), которые определяют три ветви дисперсионных соотношений:

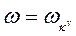(v=1, 2, 3).

Мода L соответствует продольной волне, T₁ и T₂ –поперечным (рис.6.9).

Вектор 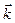меняется в интервале 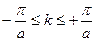и принимает столько значений, сколько элементарных ячеек содержит кристалл (т.е. n значений). Разрешенные значения κ распределены в 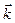-пространстве с плотностью .

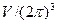В случае колебаний атомов трехмерной решетки с базисом, когда на элементарную ячейку приходится r атомов (система с 3rN степенями свободы), решение системы 3rN уравнений приводит к существованию 3 r ветвей колебаний, дисперсионные соотношения этих ветвей имеют вид:

(v=1, 2, 3; s=1, 2…r).

Три нижние ветви - акустические, остальные (3r -3) – оптические (рис.6.10).

Таким образом, движение атомов трехмерной решетки может быть представлено как суперпозиция 3rN нормальных колебаний (или мод). Каждое нормальное колебание есть гармонический осциллятор, поэтому полная энергия колебаний кристалла равна сумме энергий колебаний 3rN не взаимодействующих между собой гармонических осцилляторов.