Колебания одномерной решетки с базисом

Мы рассмотрели колебания одномерной моноатомной решетки Бравэ. Рассмотрим теперь продольные колебания атомов одномерной решетки с базисом, когда на линейную элементарную решетку Бравэ с параметром 2а приходится два атома. Пусть вдоль прямой линии располагается N ячеек. Такая система обладает 2N степенями свободы. При решении задачи о колебаниях атомов в такой системе воспользуемся следующей моделью. Рассмотрим двухатомную линейную цепочку (рис.6.7), вдоль которой поочередно располагаются атомы с различными массами M₁ и M₂, а силы между парами соседних атомов одинаковы (атомы связаны между собой пружинками одинаковой жесткости). Пружинка моделирует силы притяжения, когда она растянута, и силы отталкивания, когда она сжата.

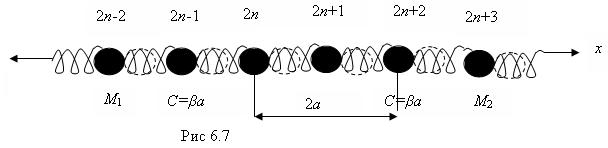
Обозначим 2na четные положения равновесия атомов с массой М₁, а (2n+1)a-нечетные для атомов с массой М₂. Пусть и_2n есть смещение атома с массой М₁ вдоль направления х в момент времени t относительно его положения равновесия, а и_2n+1 - смещение атома с массой М₂ из его положения равновесия.

Будем считать, что смещения малы в сравнении с межатомными расстояниями , а силы взаимодействия между атомами - квазиупругие. Смещения описывают продольные колебания атомов вблизи положения их равновесия.

Найдем уравнения движения атомов. Учитывая взаимодействие лишь ближайших атомов (соседних), результирующие силы, действующие на выбранные нами атомы, равны:

,

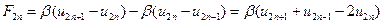
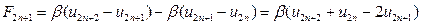где β - силовая постоянная, связанная с упругой постоянной 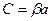. Согласно второму закону Ньютона, запишем уравнение движения:

, (6.3)

.

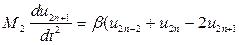Колебания атомов с различными массами будут происходить с разными амплитудами, поэтому решение уравнения будем искать в виде:

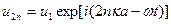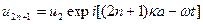; . (6.4)

Если подставить эти решения в систему (6.3), то получим

- каждому значению волнового числа κ соответствуют два значения ω, следовательно, и две моды колебаний типа (6.4). Возможные значения k ограничены соотношением:

.

При этом число допустимых неэквивалентных значений k в интервале 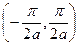равно N - числу элементарных ячеек в цепочке. Так как каждому значению k соответствуют две моды колебаний, то полное число нормальных мод в интервале 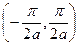равно числу степеней свободы в системе, т.е. 2N.

Решение задачи о колебаниях атомов двух сортов, таким образом, приводит к двум кривым зависимости , которые называются двумя ветвями закона дисперсии (см. рис.6.8).

Нижнюю кривую называют акустической ветвью, верхнюю - оптической. Частота оптических колебаний больше частоты акустических колебаний.

Для оптической ветви:

,

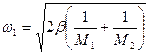для акустичeской:

.

Акустические колебания продольные, Частота стремится к нулю пропорционально k.

Длинноволновые оптические моды в ионных кристаллах могут взаимодействовать с электромагнитным излучением. При k =0 частота максимальна, с ростом k она уменьшается и при .

Таким образом, во всем интервале волновых чисел от 0 до в цепочке, состоящей из атомов двух сортов, происходит разделение колебаний на акустическую и оптическую ветви, при этом для акустических мод атомы обоих типов движутся в волне сжатия (в фазе). Для оптических мод колебаний соседние атомы движутся в противофазе.

Если рассматривать оптические колебания при малых значениях κ (длинные волны) и считать заряды атомов поочередно различными, то их колебания в противофазе вызовут смещения ионов, которые приведут к изменению электрического дипольного момента ячейки. В результате вдоль цепочки будет распространяться волна электрической поляризации с волновым числом k.