И СЫПУЧИХ СРЕД

 

 

Учебное пособие

 

 

Научный редактор – проф., канд.техн.наук С.П.Бурмасов

 

 

Екатеринбург. 2011

 

УДК 001.1:669.16.013

ББК 34.314

 

Рецензенты:

 

Старший научный сотрудник Учреждения Российской академии наук «Института металлургии» Уральского отделения РАН, канд. техн. наук Заякин О.В.

 

Доцент кафедры «Литейное производство» ФГАОУ ВПО УРФУ, канд. техн. наук Вайс И.А.

 

 

Автор: С. А. Загайнов, Е. Ю. Лозовая

 

Загайнов С. А. МЕХАНИКА ЖИДКОСТЕЙ, ГАЗОВ И СЫПУЧИХ СРЕД: Учебное пособие / С. А. Загайнов, Е. Ю. Лозовая.- Екатеринбург: ФГАОУ ВПО УРФУ, 2011. 144 с.

 

 

ISBN

 

 

Предназначено для студентов специальности 150101 – Металлургия черных металлов, всех форм обучения.

 

Библиогр.назв.6. Табл. 4. Рис.56.

 

 

УДК 001.1:669.16.013

ББК 34.314

 

ISBN

 

Ó ФГАОУ ВПО УРФУ, 2011

 

ВВЕДЕНИЕ

 

Предмет механики жидкостей, газов и сыпучих сред – это наука об основных законах поведения жидкостей, газов и сыпучих сред.

Механика жидкости, газа и сыпучих сред представляет собой дисциплину, которая является частью механики сплошной среды. Рассматривая природу и закономерности движения газообразных, жидких и сыпучих веществ, механика жидкости, газа и сыпучих сред сформировалась в самостоятельный раздел теорети­ческой механики в последнее время, объединив в себе достижения гид­ромеханики (гидравлики), газовой динамики и аэромеханики.

Для металлургов механика жидкости газов и сыпучих сред открывает законы и пути интенсифи­кации процессов производства металлов. Достижения этой науки ши­роко внедряются и в пирометаллургию и гидрометаллургию на всех стадиях подготовки шихты, выплавки металла, получения готовой про­дукции, решения экологических задач. Действительно, в условиях ме­таллургических заводов, проектных и научно-ис­следовательских институтов черной и цветной металлургии инженеру приходится решать специфические задачи, связанные с конструирова­нием, расчетом, исследованием и наладкой работы фурм доменных и других шахтных печей, продувочных фурм, используемых в процес­сах производства черных и цветных металлов; газогорелочных уст­ройств низкого и высокого давлений; мазутных и газо-мазутных фор­сунок низкого и высокого давлений; дымовых и воздушных трасс всех видов печных агрегатов; дымососов, инжекторов и дымовых труб для нагревательных и плавильных печей; газосмесительных установок инжекционного типа; теплообменников регенеративного и рекуператив­ного типов; факельных процессов, совершающихся в печах; газоочистительных устройств, стоящих за плавильными и нагревательными пе­чами, конверторами.

Предмет "Механика жидкости, газа и сыпучих сред" включает две части: механика жидкостей, газов и механика сыпучих веществ, которые тесно взаимосвязаны между собой.

В основе механики жидкости и газа лежит гидравлика как наука. Ее истоки теряют­ся в глубине тысячелетий. И это не случайно, если иметь в виду ту роль, которую сыграло использование воды в жизни человека.

Рождение научной дисциплины гидравлики обычно связывают с именем Архимеда (287–212 гг. до н.э.). Закон его имени, приведенный в трактате "О плавающих телах" (250 г. до н.э.), не претерпел практически никаких уточнений и до сих пор явля­ется одним из основных законов гидростатики. В металлургии этот закон лежит в основе методики расчета дымовых труб, некоторых видов гидравлических сопротивлений.

Второе рождение гидравлики как науки обязано гениальному итальянскому ученому эпохи Возрождения Леонардо да Винчи (1452–1519 гг.). Проповедуя учение о том, что опыт и математика являются основанием всякой научной системы, он много сделал в борьбе против средневековой схоластики, совершил ряд очень важных открытий в са­мых разнообразных областях техники, физики. Его исследования по изучению принципов работы гидравлического пресса, принципов поле­та, истечению жидкости через отверстия, вопросов движения воды в каналах, через водосливы, no-существу, положили начало эксперимен­тальной гидравлике. Поэтому справедливо признают Леонардо да Вин­чи основоположником механики жидкости.

В дальнейшем развитие гидравлики проходило с участием всемир­но-известных ученых того времени. Голландский инженер, математик С. Стивен (1548–1620 гг.) сумел определить гидростатическое давле­ние на плоскую фигуру и дать объяснение «гидростатического парадок­са». Г. Галилей (1564–1642 гг.) показал, что гидравлическое сопротив­ление зависит от скорости и плотности жидкой среды; оно возрастает с увеличением этих параметров. В результате работ Б.Кастсли (1577–1644 гг.) гидравлика обогатилась принципом неразрывности. Широко известен вклад Б. Пас­каля (1623–1662 гг.). Ему принадлежит формулировка закона, нося­щего его имя – давление на поверхности жидкости, произведенное внешними силами, передается в ней без изменения величины по всем направлениям. Гениальный английский ученый И. Ньютон (1642–1727 гг.) в своем главном труде «Математические начала натуральной философии» (1687 г.) не только обосновал свои законы механики, но и привел приближенное описание законов внутреннего трения, дал тео­ретический вывод квадратичного закона сопротивления при движении тел, установил закон динамического подобия. Законы внутреннего тре­ния, подобия применяются и сегодня при исследовании теоретических и прикладных вопросов механики жидкости и газа во многих отраслях знаний, в том числе и в металлургии.

Теоретический фундамент современной механики жидкости пост­роен в результате работ, выполненных академиками Российской ака­демии наук Л. Эйлером (1707–1783 гг.) и Д. Бернулли (1700–1782 гг.). Перу первого принадлежит трактат «Общие принципы движения жид­кости» (1755 г.), Д.Бернулли - «Гидродинамика» (1738 г.). Закон, которому присвоено его имя, устанавливал связь между давлением уровня и скоростью движения тяжелой жидкости при установившем­ся движении. Этот закон является фундаментальным в гидродинамике. Кстати, следует отметить, что термин гидродинамика впервые был вве­ден Д. Бернулли.

В это же время появились работы гениального русского ученого – М. В. Ломоносова (1711–1765 гг.) «Рассуждения о твердости и жид­кости тела» (1760 г.), «О вольном движении воздуха, в рудниках при­меченном» (1742 г.), в которых он, в частности, дал расчет естествен­ной вентиляции шахт, предложил теорию тяги дымовой трубы. Им созданы метеорологические приборы, проект и модель летательного аппарата для исследования атмосферы. Этими работами великий ученый способствовал развитию механики газа.

В XIX в. были заложены основы учения о движении вязкой жидкости. В связи с этим следует отметить работы французских уче­ных Л.Навье (1785– 1836 гг.) и Г.Стокса (1819–1903 гг.), которые получили дифференциальное уравнение пространственного движения вязкой жидкости, носящее их имена. Уравнение Навье–Стокса и се­годня широко используется для решения многих теоретических и при­кладных задач во всех областях техники, в том числе и металлургии.

Особая роль в формировании механики жидкости принадлежит английскому ученому Осборну Рейнольдсу (1842–1912 гг.). Им опре­делены условия перехода ламинарного движения в турбулентное, мно­го сделано для развития теории турбулентности, для установления принципов гидродинамического подобия, которые и в настоящее вре­мя применяются при гидро- и аэродинамическом моделировании раз­личных устройств, включая и металлургические печи, элементы их обо­рудования – горелки, трубопроводы, теплообменники и др.

Вместе с гидромеханикой в XIX в. развивалась и газовая механи­ка, фундамент которой был заложен еще работами И. Ньютона, П. Лап­ласа. Активная деятельность ученых и инженеров проявилась при ре­шении задач, связанных с созданием паровых турбин и особенно в конце века, когда возрос интерес к задачам воздухоплавания. Общепризнанна роль Н. Е. Жуковского, которого по праву называют основате­лем теоретической, технической и экспериментальной аэродинамики. Он обосновал теорему о подъемной силе, создал теорию воздушного вин­та, изобрел серию теоретических профилей крыльев, построил аэро­динамические лаборатории. Эти и другие работы не только подвели научную базу к анализу и расчету летательных аппаратов, но и ока­зали большое влияние на смежные области науки и техники – судо­строение, вентиляцию и пр. Рядом с именем Н. Е. Жуковского следует поставить имя Д. И. Менделеева (1834– 1907 гг.), который своим тру­дом «О сопротивлении жидкостей и о воздухоплавании» (1880 г.) со­здал руководство для тех, кто занимался кораблестроением, воздухо­плаванием и баллистикой, а также имя К. Э. Циолковского (1857– 1935 гг.), установившего основные формулы реактивного движения снаряда с переменной массой (первая работа по космической аэроди­намике), создал, первую аэродинамическую трубу для определения со­противления тел.

Гидродинамика, газовая динамика, аэродинамика, объединенные общим понятием механика жидкости и газа, бурно развиваются в пос­ледние десятилетия нашего времени, что в первую очередь определяет­ся темпами научно-технического прогресса. Не претендуя на полноту анализа, отметим, что к тем традиционным проблемам, которые реша­лись ранее, XX в. выдвинул новые. Это изучение сопротивления при сверхзвуковых и гиперзвуковых скоростях потока, это анализ вопро­сов движения разреженных газов, плазмы, движения сред, осложнен­ных воздействием на них электрических, магнитных, акустических по­лей, развитием процессов тепло- и массообмена. Сюда же примыкают вопросы движения многокомпонентных сред, неустановившегося дви­жения жидкости (газа), углубление представлений о турбулентности, о распространении затопленных струй и образования следа за движущимися телами и многие другие. Над решением этих проблем работа­ли и продолжают работать академики Л. И. Седов, М. Д. Миллионщиков, В. В. Струминский, А. Н. Колмогоров, П. Я. Полубаринова-Кочина, С. Лейбензон, ученые Л. Г. Лойцянский, их многочисленные учени­ки у нас в России. За рубежом широко известны работы Г. Шлихтинга, Д. Б. Сполдинга, Дж. Батчелора и др. Для – математичес­кое моделирование с помощью современных ЭВМ, постановка эксперимента на различных моделях и натурных образцах. Есте­ственно, что продолжают совершенствоваться и сами методы иссле­дования, как аналитические, так и экспериментальные.

Краткая историческая справка дает представление о развитии ме­ханики жидкости и газа как науки и ее некоторых направлений. Перечень подобных задач можно существенно продолжить, но уже из приведенного видно, что в настоящее время трудно представить себе грамотного инженера – металлурга без знаний хотя бы основ гидро- и га­зодинамики. Поэтому в металлургических вузах России почти для всех специализаций предусмотрены раз­делы механики жидкости, газов и сыпучих сред.

 

 

1. ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА

ЖИДКОСТЕЙ И ГАЗОВ

1.1. Определение жидкости

 

Жидкости (в широком смысле слова) отличаются от твердых тел легкой подвижностью частиц. В то время как для изменения формы твердого тела к нему нужно приложить конечные, иногда очень большие, силы, изменение формы жидкости может происходить под действием даже самых малых сил (жидкость течет под действием собственного веса).

Жидкость, как и всякое физическое тело, имеет молекулярное строение, т.е. состоит из молекул, расстояние между которыми во много раз превосходит размеры самих молекул, т.е. жидкость, строго говоря, имеет прерывистую структуру. В технической гидромеханике при решении большинства задач принимают жидкость как сплошную (непрерывную) среду ввиду чрезвычайной малости не только самих молекул, но и расстояний между ними по сравнению с объемами, рассматриваемыми при изучении равновесия и движения жидкости.

Жидкости по своим механическим свойствам разделяются на два класса: малосжимаемые (капельные) и сжимаемые (газообразные). С позиции физики капельная жидкость значительно отличается от газа, с позиции механики жидкости различие между ними не так велико, и законы, справедливые для капельных жидкостей, могут быть приложены также и к газам, когда сжимаемостью последних можно пренебречь.

Капельные жидкости обладают вполне определенным объемом, который практически не изменяется под действием сил. Газы же, занимая все предоставленное им пространство, могут значительно изменять объем, сжимаясь и расширяясь под действием сил. Таким образом, капельные жидкости легко изменяют форму (в отличие от твердых тел), но с трудом изменяют объем, а газы легко изменяют как объем, так и форму. Основные свойства жидкостей, существенные при рассмотрении задач технической гидродинамики, – плотность, вязкость и поверхностное натяжение.

1.2. Плотность жидкости

 

 

Плотностью жидкости (r, кг/м³)называется ее масса (М, кг), заключенная в единице объема (V, м³)

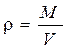. (1.1)

Плотность одна из основных физических характеристик расплава. Если жидкость неоднородна, то формула определяет лишь среднюю плотность жидкости. Для определения плотности в данной точке следует пользоваться формулой

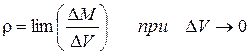(1.2)

где DM – изменение массы при изменении объема на величину DV.

Довольно часто, особенно при решении практических задач механики жидкостей и газов, используют представление о весе единицы объема g, определяя его как отношение веса вещества, заключенного в объеме, к величине этого объема, т.е.

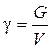.(1.3)

Вес жидкости, приходящийся на единицу объема, называется удельным весом (g, Н/м³).Плотность и удельный вес связаны между собой известным соотношением

g = r ∙ g , (1.4)

где g – ускорение свободного падения, м/с².

Данные о плотности и удельном весе некоторых жидкостей и газов приведены в табл. 1.1.

Следует подчеркнуть, что плотность и вес единицы объема жидкостей и особенно газов существенно зависят от давления и температуры.

Рассмотрим зависимость от давления. Под воздействием давления жидкость меняет свой объем. Это свойство получило название сжимаемости.

Таблица 1.1

Характеристика плотностей капельных и газообразных жидкостей

№ п/п	Наименование жидкостей	r, кг/м3	g, Н/м3
	Вода
	Чугун
	Сталь
	Шлак
	Воздух	1,205	11,821
	Оксид углерода	1,183	11,605

 

Сжимаемость капельных жидкостей под действием давления характеризуется коэффициентом объемного сжатия, который представляет собой относительное изменение объема жидкости на единицу изменения давления

,(1.5)

где V – первоначальный объем жидкости, м³; DV – изменение этого объема при увеличении давления на величину DP. Коэффициент объемного сжатия имеет размерность [Па^-1]. Знак "минус" в уравнении обусловлен тем, что положительному приращению давления соответствует отрицательное приращение (т.е. уменьшение) объема.

Для идеальных газов, т.е. газов разряженных настолько, что взаимодействие между его молекулами может не учитываться

. (1.6)

Величина, обратная коэффициенту объемного сжатия называется модулем упругости Е (Па), рассчитывается по формуле

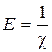. (1.7)

Модуль упругости капельных жидкостей мало меняется при изменении температуры и давления, в среднем для воды значения Е = 2×10⁹ Па.

Зависимость от температуры. Если приближенно считать, что плотность не зависит от давления, а определяется только температурой, то значение плотности для капельных жидкостей при данной температуре определяется по формуле . (1.8)

где r₀, t₀ – плотность и температура жидкости при нормальных условиях (нормальные условия: t_о = 0 ^оС, Р = 101325 Па); b_t – коэффициент температурного расширения.

Коэффициент температурного расширения b_t, выражает относительное увеличение объема жидкости при увеличении температуры на 1 град

, (1.9)

где V – первоначальный объем жидкости, м³; DV – изменение этого объема при увеличении температуры на величину DТ.

Способность жидкости менять плотность (и удельный вес) при изменении температуры широко используется для создания естественной циркуляции в котлах, отопительных системах, для удаления продуктов сгорания.

В отличие от капельных жидкостей газы характеризуются значительной сжимаемостью и высокими значениями коэффициента температурного расширения. Зависимость плотности от давления и температуры устанавливается уравнением состояния.

Для идеальных газов справедливо уравнение Клапейрона

, (1.10)

где Р – абсолютное давление, Па; R_уд – удельная газовая постоянная, различная для разных газов, но не зависящая от температуры и давления (для воздуха R_уд = 287 Дж/кг.К); Т – абсолютная температура, К.

Поведение реальных газов в условиях, далеких от сжижения, незначительно отличается от поведения идеальных газов, и для них в широких пределах можно пользоваться уравнением состояния идеальных газов.

Плотность газа, при фактических температуре и давлении, можно определить по уравнению

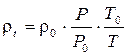, (1.11)

где r₀, Р₀, Т₀ – плотность, давление и температура газа в стандартных условиях (для воздуха стандартные условия t₀ = 293 К, Р₀ = 101325 Па; r₀ = 1,205 кг/м³).

Многофазные – это системы, состоящие из нескольких фаз. Иногда их называют гетерогенными системами. Все металлургические системы являются гетерогенными. Простейшим случаем многофазной системы являются двухфазные системы. Например: газ-твердые частицы (пневмотранспорт, пылеулавливание), газ-капли жидкости (распылители, газовые сушилки). Во всех этих примерах первая из указанных фаз (основная) условно называется непрерывной, вторая - дискретной.

Количество дискретной фазы в непрерывной определяется объемной концентрацией (b). Обычно за объемную концентрацию принимается отношение объема, занятого дискретной фазой, к общему объему многофазной системы.

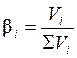_. (1.12)

Среднюю плотность двухфазной системы можно представить в следующем виде

r = b ∙ r₂ + (1 − b) ∙ r₁ , (1.13)

где r₂ и r₁ – плотности соответственно дискретной и непрерывной фаз.

1.3. Вязкость жидкостей

 

Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу. Вязкость – характеристика сил внутреннего трения. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц жидкости. Наряду с легкоподвижными жидкостями (водой, воздухом) существуют очень вязкие жидкости, сопротивление которых сдвигу весьма значительно (глицерин, тяжелые масла и др.). Таким образом, вязкость характеризует степень текучести жидкости или подвижности ее частиц.

Вязкость или текучесть жидкостей, в том числе расплавленных металлов и шлаков является их важнейшим физическим свойством.Вязкость жидкости связана с ее структурой и определяется межчастичным взаимодействием, поэтому ее изучение, наряду с другими физико-химическими свойствами, позволяет оценить строение металлических и шлаковых расплавов, природу и силы взаимодействия между компонентами в сплавах, а также связь между твердым и жидким состоянием.

Вязкость шлаков и металлов в значительной мере определяет скорости различных физико-химических процессов, особенно диффузионные явления в расплавах. От значения вязкости зависит чистота получаемого металла: скорость удаления газов и неметаллических включений. Вязкость металла влияет на выбор режима разливки, определяет условия формирования слитка, заполняемость литейных форм. Существует связь между вязкостью жидкого металла и процессом его кристаллизации, а следовательно и свойствами твердого металла.

Пусть жидкость течет вдоль плоской стенки (рис.1.1), как это наблюдается при ламинарном течении.

 

 

Y,м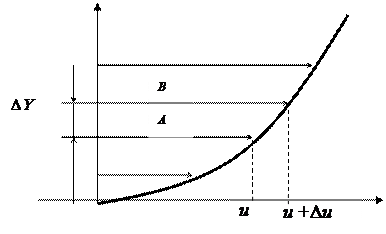

 

Рис. 1.1. Распределение скоростей при течении жидкости вдоль плоской стенки

 

 

u, м/с

 

Вследствие тормозящего влияния стенки слои жидкости будут двигаться с разными скоростями, значения которых возрастают по мере отдаления от стенки. Рассмотрим два слоя жидкости, двигающихся на расстоянии DU друг от друга. Слой А движется со скоростью u, а слой В со скоростью u + Du (за единицу времени). Величина Du является абсолютным сдвигом слоя А по слою В, а (Du/DU) есть градиент скорости (относительный сдвиг). Появляющееся при этом движении касательное напряжение (сила трения на единицу площади) обозначим буквой t[Н/м²]. Тогда аналогично явлению сдвига в твердых телах можно предположить зависимость между напряжением и деформацией, впервые установленной И.Ньютоном

, (1.14)

где t − напряжение сдвига, Н/м²; h − коэффициент динамической (абсолютной) вязкости, Па×с; du − изменение скорости; dY − изменение направляющей к нормали скорости.

Выражение (1.14) называется законом вязкости Ньютона. Жидкости, для которых справедлив закон трения Ньютона, называются ньютоновские.

Коэффициент динамической вязкости h (Па.с) для различных жидкостей, расплавленных металлов и шлаков имеет следующие значения:

 

Вода (25^оС) …0,00089 Железо (1600^оС) ….0,0045

Глицерин (20 ^оС) …1,499 Сталь (1600 ^оС) ….0,0050

Алюминий (700 ^оС)…0,00113 Шлак:

Медь (1300 ^оС) …0,0041 доменный (1500 ^оС)…..0,2-0,6

мартеновский (1600 ^оС)…0,02-0,04.

Аномальные жидкости – это такие жидкости, которые не подчиняются закону вязкости Ньютона (1.14). К этим жидкостям можно отнести, например, литой бетон, строительный раствор, нефтепродукты при температуре близкой к застыванию и др.

Чтобы привести такие жидкости к движению, необходимо приложить некоторое (иногда значительное) усилие. Движение аномальных жидкостей начинается только после того, как касательные напряжения в них достигнут некоторого предельного значения (так называемое начальное напряжение сдвига), при меньших касательных напряжениях эти жидкости не текут, а испытывают только упругие деформации, как твердые тела.

В аномальных жидкостях касательное напряжение определяется по формуле Бингема

, (1.15)

где t₀ – начальное, предельное напряжение сдвига (для ньютоновских жидкостей равно нулю).

Таким образом, в аномальных жидкостях сила трения возникает еще в покоящихся, но уже стремящихся прийти в движение жидкостях.

Вязкость жидкостей в большей степени зависит от температуры, при этом вязкость капельных жидкостей при увеличении температуры уменьшается, а вязкость газов возрастает (например, с увеличением температуры от 0 до 100^оС вязкость воды уменьшается почти в 7 раз).

Наряду с понятием абсолютной или динамической вязкости в гидравлике находит применение понятие коэффициента кинематической вязкости (n, м²/с), представляющей собой отношение динамической вязкости жидкости к ее плотности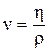. (1.16)

Коэффициент кинематической вязкости характеризует ускорение частиц под влиянием сил вязкости.

Для капельных жидкостей коэффициент кинематической вязкости практически не зависит от давления, а для газов с ростом давления падает. Зависимость от температуры аналогична зависимости коэффициента динамической вязкости.

Подсчет n смеси газов может быть осуществлен по формуле

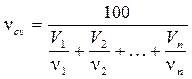, (1.17)

где V₁, V₂, V_n − объемное содержание компонентов газовой смеси (%); n₁, n₂,…, n_п − их коэффициенты кинематической вязкости. Точное значение вязкости смеси газов или жидкостей может быть найдено только экспериментальным путем.

С понятием вязкости связано понятие сила внутреннего трения в жидкости (F_h) это величина прямо пропорциональна градиенту скорости (du / dY), площади трущихся слоев (S) и динамической вязкости

. (1.18)

1.4. Поверхностное натяжение жидкости

(или поверхностные явления в сталеплавильных процессах)

При производстве чугуна и стали поверхностные явления играют важную, а иногда и решающую роль. Поверхностные явления в жидких металлических и неметаллических расплавах, на границах раздела расплав-твердая фаза и высокодисперсных твердых телах имеют большое значение для многих технологических процессов черной и цветной металлургии, порошковой металлургии, полупроводниковой техники, технологии сварки, пайки и др. областей. Результаты исследований поверхностных явлений широко используются при решении теоретических вопросов жаропрочности, ползучести, спекания, пропитки, модифицирования и др.

Молекулы жидкости, расположенные у поверхности контакта с другой жидкостью, газом или твердым телом, находятся в условиях, отличных от условий молекул, находящихся внутри некоторого объема жидкости. Внутри объема молекулы окружены со всех сторон такими же молекулами, вблизи поверхности - лишь с одной стороны, поэтому энергия поверхностных молекул отличается от энергии молекул, находящихся в объеме жидкости, на некоторую величину, называемой межфазной поверхностной энергией (Э, Дж). Эта энергия пропорциональна площади поверхности раздела (S, м²)

Э = S × s, (1.19)

где s – коэффициент пропорциональности или коэффициент поверхностного натяжения (Н/м или Дж/м²), зависит от природы соприкасающихся сред.

Этот коэффициент можно представить в виде

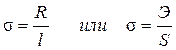, (1.20)

где R – сила поверхностного натяжения, Н; l – длина линии, ограничивающей поверхность раздела, м.

Выражение (1.20) характеризует свободную энергию единицы поверхности или удельную поверхность.

Поверхностное натяжение жидкости чувствительно к ее чистоте и температуре. При повышении температуры поверхностное натяжение уменьшается, а в критической точке перехода жидкости в пар обращается в нуль.

Величина коэффициента поверхностного натяжения (s) характеризует прочность межчастичных связей в жидкости, следовательно, с понятием «поверхностное натяжение» связаны следующие явления:

1. Работа когезии (W_к) – это изменение свободной энергии системы при разделении одной фазы

W_к = DF = (F + 2s) – F = 2s. (1.21)

2. Работа адгезии (W_А) – это изменение свободной энергии системы при разделении двух фаз по границе раздела

W_А = DF = (F + s₁ + s₂) – (F + s₁₂) = s₁ + s₂ - s₁₂. (1.22)

3. Адсорбция – это явление изменения концентрации вещества в поверхностном слое по сравнению с концентрацией вещества в объеме.

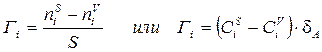,(1.23)

где n^S_i , n^V_i – количество молей i-того компонента в поверхностном слое и объеме фазы; S – площадь поверхности раздела; C^S_i , C^V_i – концентрация i-того компонента в поверхностном (адсорбционном) слое и объеме фазы; d_А – толщина адсорбционного слоя.

По силе взаимодействия различают физическую и химическую адсорбцию. Если частица в поверхностном слое при температуре меньше 250^оС образует слабые реакции, то это физическая адсорбция. Если адсорбирующая частица образует устойчивые связи с соседними, то это химическая адсорбция.

4. Поверхностно-активные вещества.

В растворах силы взаимодействия между различными частицами не одинаковы. В связи с этим, слабовзаимодействующие частицы вытесняются на поверхность, что приводит к изменению величины поверхностного натяжения и явление это протекает самопроизвольно.

Вещества, вытесняемые на поверхность и снижающие поверхностное натяжение, называют поверхностно-активными. Малое содержание поверхностно-активных веществ в объеме приводит к насыщению ими поверхностного слоя и соответствует положительной адсорбции.

Вещества, повышающие поверхностное натяжение жидкости, называют поверхностно-инактивными и соответствуют отрицательной адсорбции.

Для железа поверхностно-активными частицами являются сера и кислород – они связаны с окружающими слабо и выталкиваются в поверхностный слой. Концентрация серы и кислорода в поверхностном слое больше, чем в объеме примерно в 200-300 раз.

 

1.5. Явление смачивания

 

Поверхностное натяжение жидкостей влияет на явление смачивания.

Рассмотрим рис. 1.2 – схемы смачивания жидкостью твердой стенки сосуда. На границе раздела фаз между поверхностью жидкости и твердой стенкой образуется, так называемый краевой угол (q ), который зависит от природы соприкасающихся тел и не зависит от формы поверхности и от действующих сил тяжести. Если край жидкости приподнят, ее поверхность имеет вогнутую форму (рис. 1.2 а), и острый краевой угол. В этом случае жидкость смачивает твердую поверхность. Чем хуже смачивающая способность жидкости, тем больше краевой угол. Если q > 90^o, то жидкость считается не смачивающей (рис. 1.2 б). При полном не смачивании (q = 180^о) капли жидкости как бы поджимаются, стараясь уменьшить площадь контакта с твердой поверхностью.

 

		Рис. 1.2. Схемы смачивания жидкостью твердой стенки: а – хорошее смачивание; б – плохое смачивание .

 

.

 

 

Рассмотрим схему смачивания каплей подложки (рис. 1.3).

Рис. 1.3. Схема смачивания каплей жидкости твердой подложки

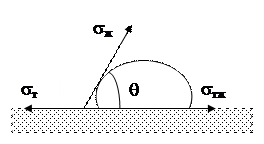
Если в точке касания провести касательные и величину поверхностного натяжения (s) представить в виде суммы сил, то при равновесии системы справедливо выражение, характеризующее закон Юнга

s_т = s_ж · Соsq + s_{т - ж}. (1.24)

Следовательно 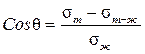.(1.25)

Из выражения (1.25) следует, что если s_т > s_{т - ж}, то Сosq >0, и следовательно q < p /2, т.е. наблюдается хорошее смачивание поверхности. В противоположном случае Сosq <0, следовательно q > p/2, т.е. плохое смачивание поверхности

Из уравнения (1.22) известно, что работа адгезии W_А = s_т + s_ж – s_{т - ж},, следовательно W_А – s_ж = s_т – s_{т - ж} и

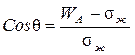_.(1.26)

Определяя s_ж и Сosq экспериментальным путем, можно найти работу адгезии, характеризующую прочность сцепления между жидкостью и твердой поверхностью из выражения (1.26).

На основе лабораторных экспериментов установлено, что при температуре 1550^оС железо плохо смачивает огнеупорные оксиды Al₂O₃ и MgO (q » 140^о).

Добавка других элементов к железу вызывает снижение величины краевого угла смачивания. Особенно сильное влияние оказывают сера и кислород. Эти элементы хорошо растворяются в обеих фазах и снижают краевой угол q, т.е. улучшают смачивание.

От явления смачиваемости зависит поведение жидкости в тонких (капиллярных) трубках, погруженных в жидкость. При смачивании жидкость в трубке поднимается над уровнем свободной поверхности, при не смачивании опускается. Высота капиллярного поднятия (опускания) жидкости определяется

 

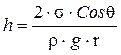, (1.27)

где r − радиус капилляра, м.

Угол q между водой и стеклом практически равен нулю, если поверхность очень чистая. Влияние сил поверхностного натяжения приходится учитывать при работе с жидкостными приборами для измерения давления, при истечении жидкости из малых отверстий, при фильтрации и др.

 

1.6. Дисперсные системы

 

Любое вещество можно привести в состояние той или иной степени измельчения. Вещество, находящееся в состоянии измельчения, называется дисперсной фазой.

Среду, в которой находится дисперсная фаза, называют дисперсной средой.

В зависимости от степени измельчения меняется доля частиц на поверхности и, в связи с этим, доля поверхностных свойств вещества. При размере частиц 10^-5−10^{-7 см поверхностные свойства веществ оказываются решающими.}

По степени измельчения дисперсные фазы можно классифицировать следующим образом:

R > 10^{-5 см} – грубое диспергирование;

10^-5 > R > 10^{-7 см} – коллоиды;

R < 10^{-7 см} – молекулярное диспергирование.

По агрегатному состоянию различают следующие дисперсные системы (табл. 1.2).

В жидкой стали содержится большое число твердых, жидких и газообразных включений. Шлаковая пена может содержать до 90 % газовой фазы.

 

Таблица 1.2

Дисперсные системы

Дисперсная среда	Дисперсная фаза	Дисперсная система
Жидкость	Твердая	Суспензии
Жидкость	Жидкая	Эмульсии
Жидкость	Газ	Газовые эмульсии (пены)
Газ	Твердая	Дымы, пыли
Газ	Жидкая	Туман

 

1.7. Вспенивание, физические эффекты при вспенивании

 

Вспенивание шлака – не желательное технологическое осложнение. Во вспененном шлаке резко снижается скорость тепло- и массообменных процессов. Например, коэффициент теплопроводности для кипящих шлаков l_эф = 116−232 Вт/м.град, то для вспененных шлаков l_эф = 5−7 Вт/м.град.

Вспенивание шлака определяется изменением свободной энергии

DG = s_{ш - г} × S_П ^S, (1.28)

где s_{ш - г} – поверхностное натяжение между фазами шлак-газ, Дж/м²; S^S_П – суммарная поверхность пузырей, м².

Исчезновение пены связано со слиянием газовых пузырьков и их металлических оболочек. При оседании пены происходит большой выигрыш энергии. Однако слиянию пузырей препятствуют следующие физические эффекты:

1. Расклинивающий эффект связан с тем, что при вспенивании, поверхностные слои пены обогащаются, относительно крупными слабыми и поверхностно-активными ионами (SiO^4-₄; Si₂O^6-₇; PO^3-₄ и др.). Поверхностно-активные ионы имеют одинаковый заряд и при сближении оболочек отталкиваются, препятствуя слиянию и этим стабилизируют пену.

2.Кинетический эффект связан с диффузией поверхностно-активных вещества (ПВ) в участки вновь образованной поверхности. Рассмотрим рост газового пузыря в объеме шлака (рис. 1.4).

 

 

Рис. 1.4. Влияние кинетического эффекта на слияние двух пузырей