Определение скорости осаждения (всплывание) твердых частиц

Рассмотрим осаждение твердой тяжелой частицы в неограниченном объеме вязкой жидкости (рис. 6.2); в начальный момент скорость движения частицы u = 0. Воспользуем­ся уравнением движения в виде

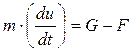, (6.3)

где m -масса частицы с учетом присоединенной массы жидкости; (du / dt) - ускорение движения твердой частицы; G - вес частицы с учетом влияния архимедовой силы; F - сила лобового сопротивле­ния.

Участок стабилизации скорости при свободном осаж­дении относительно мал, поэтому основной участок час­тица проходит равномерно с постоянной скоростью - скоростью равномерного свободного осаждения (всплывания) твердого тела в жидкости, называемой гидравли­ческой крупностью. Аналогом гидравлической крупности применительно к обтеканию свободной частицы воздуш­ным потоком является скорость витания.

Скорость равномерного осаждения или всплывания твердого тела в жидкости легко определяется из урав­нения (6.3), которое для участка равномерного движе­ния упрощается в связи с равенством нулю ускорения (du / dt = 0). Рассмотрим случай осаждения сферической твердой частицы в вязкой жидкости (рис. 6.2). Вес частицы с учетом силы Архимеда определяется по уравнению

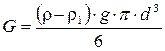, (6.4)

где r и r₁ - соответственно плотности твердой частицы и жидкости; d - диаметр частицы.

Очевидно, что при всплывании твердой частицы в уравнении следует записать первый сомножитель в виде (ρ₁ - ρ).

Сила лобового сопротивления в соответст­вии с формулой (6.1) определится в виде

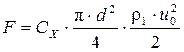, (6.5)

где u_o - скорость равномерного движения твердой частицы.

Рис. 6.2. Осаждение твердой сфе­ры в вязкой жидкости

Приравнивая правые части выражений (6.4) и (6.5) и решая полученное уравнение относительно ско­рости u0, получим 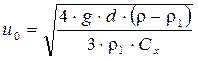. (6.6) Уравнение (6.6) при известном Cx позволяет опреде­лить скорость витания в зависимости от конкретных условий решаемой задачи. Недостатком этого уравнения является неопределен­ность коэффициента лобового сопротивления Сх, завися­щего, как известно, от числа Рейнольдса (рис.6.1), которое вычис­ляется по скорости осаждения или всплывания u0.

При движении весьма малых частиц (d < 1 мм и C_x = 24 / Re) урав­нение (6.6) приобретает вид уравнения Стокса

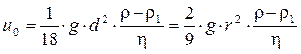, (6.7)

где h - коэффициент динамической вязкости, Па×с.

При расчете скорости равномерного движения частиц, имеющих форму, отличную от сферической, вводится по­нятие диаметра, эквивалентного по объему, или диамет­ра, эквивалентного по площади поверхности шара.

В этом случае расчет усложняется, однако и здесь для первого приближения можно использовать уравне­ния, подставляя в них значения эквива­лентного диаметра, например по объему, и соответству­ющий форме частицы коэффициент лобового сопротив­ления.

За пределами закона Стокса уравнение обычно решается методом подбора или графически. В критериальной форме зависимость скорости осаждения, всплытия частиц выражается

Re = f(Ar), (6.8)

где Re - число Рйнольдса (Re = d × ρ₀ / η); Ar - число Архимеда (Ar = g × d ³× (ρ –ρ₁) / (ρ₁ × n²)).

Рис.6.3. Зависимость Re = f(Ar) для равномерного осаждения

(всплывания) твердой сферы в вязкой жидкости

 

С помощью графика этой зависимости (рис.6.3) гидравлическая крупность сферических частиц опре­деляется без затруднений, т.к. критерий Архимеда для заданного диаметра сферы однозначно опре­деляет значение критерия Рейнольдса, из которого и находится гидрав­лическая крупность. Эксперимен­тальные графики, аналогичные гра­фику зависимости (6.3), могут быть легко построены для частиц любой формы. Графическая зависимость Re = f(Аr) аппроксимируется прибли­женными формулами, которые имеют хорошее подтверждение в опытах не только для равномерного осаждения (всплывания) одиноч­ных частиц, но и для стесненного (массового) их осаждения

, (6.9)

или

, (6.10)

где k и l - безразмерные экспериментальные постоянные, завися­щие от формы частиц (для сферических частиц k = 27,27; l = 3,03); e = 1 - b (здесь b - объемная концентрация твердых частиц).

Обобщенное уравнение (6.9) справедливо для любо­го гидравлического режима осаждения, уравнение (6.10) - только для переходного режима при l < Re < <10³.

 

6.2. Особенности осаждения (всплывания) капель жидкости

и газовых пузырей

 

В системах вентиляции и кондиционирования возду­ха, в контактных теплообменных аппаратах приходится исследовать и рассчитывать процессы взаимодействия капель жидкости и газовых пузырей с окружающими их жидкостью или газом. Особенность движения капель и пузырьков в жидкой или газовой среде обусловливается главным образом тремя факторами: способностью непрерывно изменять свою форму в процессе движения, наличием циркуля­ции жидкости или газа внутри капли или пузырька, воз­можностью изменения условий на границе раздела в связи с фазовыми переходами или химическими реак­циями. Способность капли деформироваться при движении определяется в первую очередь разностью давления вну­три капли и в окружающей ее среде жидкости. Извест­но, что в капле под действием сил поверхностного натя­жения возникает положительное приращение давления в соответствии с уравнением Лапласа

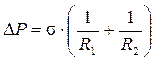, (6.11)

где DР = Р - Р_о – разность давления внутри капли и в окружающей среде (величина практически постоянная при постоянном объеме; R₁ и R₂ – главные радиусы кривизны поверхности раздела фаз; s – коэффициент поверхностного натяжения.

Разность давления DR при движении сферической кап­ли не влияет на характер ее движения. Капля движется, как твердый шар. Однако форма капли остается сфериче­ской при очень малых ее размерах (d £ l мм). Капля больших размеров, отрываясь от насадка (рис. 6.4 а), начинает деформироваться, принимая форму шара (рис. 6.4 б), потом симметричного (рис. 6.4 в) и затем деформированного (рис. 6.4 г) сфероида. Деформация капли происходит вследствие неравномерного распреде­ления давления по ее внешней поверхности. Капли сравнительно небольшого размера, осаждающиеся (всплывающие) с малой скоростью (Re £ l), испытыва­ют давление со стороны окружающей жидкости, равно­мерно распределенное по поверхности капли. При этом приращение давления DR не влияет на форму капли. Увеличение размеров капли, а следовательно, и скоро­сти ее осаждения (всплывания), приводит к нарушению равномерности в распределении внешнего давления на ее поверхности. В этом случае - в области разрежения возникает равнодействующая сила давления, направлен­ная в сторону окружающей каплю среды. Минимальное внешнее давление наблюдается в точках максимальных скоростей обтекания, т.е. в критических точках 2 и 4, расположенных на границе экваториальной плоскости сферы. Поэтому и максимальная деформация происхо­дит в плоскости, нормальной к направлению движения капли (см. рис. 6.4 в, г). Степень деформации капли вдоль оси движения зависит от разности между внешним (со стороны окружающей жидкости) давлением и давлением в капле. Так как DR практически не меняется при изменении формы капли постоянного объема, при увеличении разрежения в кормовой области (точка 3), кривизна этой части поверхности становится больше, чем в лобовой (точка 1). С увеличением скорости дви­жения капли разность между динамическим давлением (r × u²_o / 2) и приращением давления

 

Рис. 6.4. Деформация жидкой капли при ее падении в воздухе или в несмешивающейся с ней жидкости

внутри обтекаемой капли возрастает. В этом случае в лобовой части капли кривизна ее поверхности может стать отрицательной (рис. 6.4 г); увеличение кривизны может привести к разрушению капли. Изменение формы капли, естественно, увеличивает сопротивление ее движению. Подвижность поверхности капли обусловлена наличием силы трения на ее поверхности. Так как касательные напряжения по обе стороны от поверхности раздела фаз равны между собой, внутри капли развивается цир­куляционное течение, скорость циркуляции при этом увеличивается с возрастанием размера капли. В качест­ве критерия, определяющего начало и степень циркуля­ции внутри капли, обычно принимается критерий Бонда , (6.12) где d - усредненный диаметр капли.

Начало деформации капли соответствует значениям числа В ³ 0,4, заметная циркуляция - приблизительно В = 1–1,5. Наличие циркуляции жидкости внутри капли умень­шает сопротивление ее движению.

На изменение величины лобового сопротивления кап­ли (или пузырька газа) в значительной степени влияет присутствие в окружающей среде поверхностно-актив­ных веществ (например, солей кальция, магния и т.п.). В присутствии поверхностно-активных веществ, движе­ние капли жидкости или пузырька газа сферической формы практически не отличается от движения твердого шара. При взаимодействии химически чистых фаз скорость капель небольшого диаметра (Re £ l) может быть вычислена по аналитической формуле Рыбчинского – Адамара

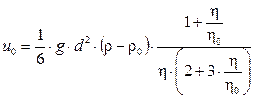, (6.13)

где h, h_o – соответственно коэффициенты динамической вязкости капли (пузырька) и среды.

Исключения:

1. В присутствии поверхностно-активных веществ, су­щественно уменьшающих подвижность границы раздела фаз (в этом случае можно положить h ® 0), формула (6.13) переходит в уравнение Стокса (6.7).

2. При больших значениях числа Рейнольдса расчет равномерного осаждения (всплывания) капель и пузы­рей можно производить по формулам (6.7), (6.9) и (6.10). Однако следует помнить, что при Re >10³ кри­вая C_x = f(Re) для капель жидкости начинает отходить от аналогичной кривой для твердого шара, приближаясь к кривой для круглого диска, установленного поперек набегающего потока.

3. При крупности пузырей менее 1 мм, их скорость всплывания рассчитывается по уравнению Стокса (6.7).

 

 

7. ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА СЫПУЧИХ МАТЕРИАЛОВ

 

7.1. Основные понятия и определения

 

Шихтовые материалы, используемые при производстве металлов, огнеупорные порошки, ферросплавы и другие сыпучие представляют собой совокупность крупных и мелких кусков.

В технической литературе такие материалы называют часто сыпучими и кусковыми или просто сыпучи­ми материалами. Все эти названия употребляют как синонимы.

К идеально сыпучим материалам относят песок, зерно, т.е. сыпучие материалы, представляющие собой совокупность большого числа мелких твердых частиц одного и того же размера относительно правильной формы с минимальной связью между ними. Идеально сыпучее тело очень подвижно, легко истекает из отверстий, обла­дая, как это принято называть, хорошей сыпучестью.

Шихтовые материалы по своим физико-механическим свойствам отличается от идеально сыпучего материала, во-первых, неоднород­ностью размеров кусков, и во-вторых, связью между частицами.

Изучение физических свойств шихтовых материалов необходимо для правильного понимания явлений выпуска. Только на этой ос­нове можно объективно решить, в какой мере применимы зако­номерности выпуска сыпучих тел к движению шихтовых материалов. Изучение свойств шихтовых материалов при их загрузке в емкости и их истечении из бункеров лежит в основе проектирования систем загрузки.

Принята следующая классификация материалов в зависимости от их крупности:

- галька, камни - >20 мм;

- гравельные частицы - 2-20 мм;

- песчаные частицы: крупные 2-1 мм, средние 1-0,25 мм, мелкие 0,25 –0,05 мм;

- пылеватые частицы <0,05 мм;

- глинистые частицы < 0.005 мм.

Как известно из механики, свойства шихтовых материалов, определяются, в первую очередь гранулометрическим соста­вом и влажностью.

Если в сыпучем материале преобладает одна какая-либо группа частиц, то и материал, в целом, приобретает свойства этой группы. Изучение свойств отдельных фракций шихтовых материалов дает возможность произвести каче­ственную оценку однородных шихтовых материалов.

Приобретение сыпучим материалом определенных свойств в зависи­мости от его гранулометрического состава наблюдали при лабораторных опытах. Например, кусковые руды в разрыхленном состоянии обладают подвижностью и при условии нормальной проходимости свободно выпускаются из рудоспусков и люков. Связность кусковой руды ничтожна, между ее частицами имеются только силы трения.

Большие размеры кусков руды затрудняют ее истечение вслед­ствие того, что они оказывают статическое сопротивление изме­нению их естественного расположения (вращению, опрокидыва­нию и т.д.). Определенную роль при этом играет и форма кусков (кубо-образная или плитчатая).

Наблюдаемое в лабораторных условиях ухудшение условий выпуска при увеличении содержания в смеси пылеватых и глини­стых частиц (менее 0,05 мм) происходит и при выпуске сыпучих в производственных условиях. Сыпучие материалы с большим содержанием мелочи интенсивнее зависают. Особенно это заметно для угля или шихты крупностью 0-5 мм.

Ухудшение условий выпуска сыпучих с увеличением содержания пылеватых и глинистых частиц подчи­няется общим физическим законам. Исследования показывают, что силы сцепления отдельных частиц значи­тельно возрастают при уменьшении их размеров мельче 0,05 мм и, особенно за пределами 0,005 мм (глинистые частицы).

При увеличении влажности сыпучего материала силы сцепления увеличива­ются только до известного предела (до насыщения влагой сыпу­чего материала и перехода его в плывун).

Влияние влажности на смесь неодинакового состава различно. Для шихтовых материалов содержание влаги редко достигает величины, вызывающей переход их в плывучее состояние.

Для оценки сыпучих свойств руды, т.е. при оцен­ке ее способности к выпуску, необходимо знать ее основные фи­зико-механические свойства.

7.2. Физико-механические свойства шихтовых материалов

Кусковатость или гранулометрический со­став шихтовых материалов характеризует количественное распределение кусков руды по их крупности.

Гранулометрический состав руды определяют просеиванием на грохотах или фотопланиметричесиим методом. В зависимости от гранулометрического состава шихтовые материалы делятся на кусковые и мелкие. Для кусковых шихтовых материалов харак­терно преобладание фракции более 5 мм. Мелкие шихтовые материалы содержат наряду с крупными кусками 50-60 % фракции менее 5 мм. Для мелких руд характерно содержание так называемых пы­леватых и глинистых частиц. Форма кусков шихтовых материалов оказывает вли­яние на ее сыпучие свойства.

Проходимость. Выпуск шихтовых материалов требует определенного соотношения между размерами отверстий и размерами кусков. Это соотношение называют проходимостью. Проходимость круп­ных кусков руды через выпускные отверстия характеризует отношение минимального сечения выпускных отверстий к макси­мальному размеру кусков руды. По данным ряда исследований, это отношение должно быть не менее 3-5. При нарушении этого условия в выпускных отверстиях могут образо­вываться зависания (заторы) шихтовых материалов, ухудшающие процесс выпуска. Частота зависаний зависит от процентного соотношения крупных кусков в общей массе шихтовых материалов. Кусковатость шихтовых материалов зависит от ее крепости, хрупкости, минерало­гического состава и может регулироваться технологической схемой дробления.

Сводообразование - самопроизвольное возникновение в сыпу­чей массе над выпускным отверстием сводов естественного рав­новесия. Образование сводов обусловливается размерами выпускного отверстия и связностью шихтовых материалов, зависящей от гранулометрического состава, содержания в ней пылеватых и глинистых частиц, влажности и разрыхления. Сводообразование может возникать даже в идеально сыпу­чих материалах.

Хрупкостьюобрушенной руды называют ее свойство измельчаться при выпуске и доставке.

Влажность обрушенной руды (гигроскопическая влажность - влага, впитываемая ча­стицами из окружающего воз­духа и содержащаяся в руде после дренажа) оказывает су­щественное влияние на сыпу­чие свойства ру­ды. Если преобладают крупнокусковые фракции (более 3 мм), влияние, оказываемое содержанием влаги на сыпучие свойства, мало ощутимо.

При рудах, содержащих пылеватые и глинистые частицы, влияние содержания влаги на сыпучие свойства обрушенной ру­ды сказывается весьма заметно. Так, сыпучие свойства криворожских руд при содержании влаги 3-8 % и частиц меньше 0,05 мм более 20 % настолько ухудшаются, что выпуск их почти невозможен.

Содержание влаги определяют по формулам:

, (7.1)

, (7.2)

где W - искомая влажность, %; M_вл- масса порции руды до просушивания; М_сух - масса порции руды после просушивания.

Липкостью рудных материалов называется их свойство при­липать к поверхности выпускных отверстий, а также образовы­вать комки, нарушающие процесс выпуска. Липкость рудных материалов зависит от содержания влаги и минералогического состава. Содержание глинистых частиц в руде является причиной ее лип­кости.

Сцепление.Силы сцепления, препятствующие как взаимному отрыву одной части сыпучего материала от другой, так и их взаимному сдвигу, возникают при наличии цементирующих веществ или вла­ги. В сухих сыпучих материалах некоторое сцепление возникает благодаря тому, что частицы зацепляются друг за друга своими неровностями и заклинивают друг друга.

Силы сцепления зависят от формы и размеров частиц, влаги и давления. С увеличением содержания в сыпучем материале пылеватых и глинистых частиц сцепление растет. Оно возрастает также с увеличением плотности сыпучего материала.

Слеживаемостью рудных материалов называют их уплотнение под влиянием собственного веса и горного давления.

Слеживаемость проявляется в рудах, содержащих более 10 % частиц размером 0-0,05 мм при влажности 3-8 %, а также при механическом смешивании руды с глиной или мягкими сланцами. Сухая смесь руды с глиной свободно проходит через выпускные отверстия. При увеличении содержания влаги до 2- 3 % наблюдается слеживание.

Слеживаемость характеризуется резким ухудшением сыпучих свойств руды, ухудшением истечения ее из выпускных отверстии.

Плотность шихтовых материалов может характеризоваться удельной, кажущейся и насыпной плотностью.

Удельная плотность – это плотность шихтового материала. Кажущаяся плотность – это плотность куска шихтового материала, определяется по формулам:

, (7.3)

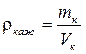, (7.4)

где V_п - объем пор в куске, м³; V_к – объем куска материала, м³; m_к – масса куска, кг.

Насыпная плотность – это плотность слоя, определяется по формуле

, (7.5)

где V_слоя - объем слоя сыпучих, м³; m_слоя – масса слоя, кг.

Плотность шихтовых материалов характеризуют коэффициентом плотности укладки

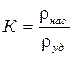, (7.6)

где r_нас - насыпная плотность, т/м³; r_уд - удельная плотность, т/м³.

Для руды, как и для любого сыпучего материала, суще­ствует своя минимальная и максимальная плотность укладки. Для сыпучего материала, состоя­щего из стальных шаров одного размера, коэффициент плотности изменяется от максимума 0,742 до минимума 0,542.

Влияние динамического характера засыпки материала на плотность шихтовых материалов возрастает с увеличением высоты паде­ния. Однако, как только величина коэффициента плотности дости­гнет максимума, влияние этого эффекта уже не сказывается. Это очень важное положение, имеющее большое практическое значе­ние.

Практика достаточно убедительно показывает, что увеличение плотности сыпучего материала и обусловленный этим рост коэффициен­та внутреннего трения затрудняют выпуск шихтовых материалов.

Коэффициент разрыхления. Для руды и вообще для сыпучих материалов между объемным весом в массиве и в разрыхлен­ном состоянии существуют определенные соотношения, характери­зуемые коэффициентом разрыхления

, (7.7)

где r_нас – насыпная плотность, т/м³; r_р – плотность в разрыхленном состоянии, т/м³.

Величина коэффициента разрыхления зависит от гранулометрического состава сыпучего материала. С увеличением содержа­ния крупнокусковых фракций коэффициент разрыхления возрас­тает.

Разрыхление сыпучих непостоянно. Под влиянием собственного веса и динамических на­грузок шихтовые материалы уплотняется. Чем лучше разрыхлена руда, тем лучше ее сыпучие свойства, тем успешнее протекает выпуск.

Шихтовые материалы разрыхляются также в начальный период выпуска. Поэтому различают кроме первичного разрыхления по­сле отбойки и вторичное разрыхление в процессе выпуска.

Коэффициент внутреннего трения. Статическое состояние сыпучего материала может быть выражено

τ = τ₀ × tg φ, (7.8)

где τ - сопротивление сдвигу; τ₀ - начальное сопротивление сдвигу; φ – угол внутреннего трения сыпучей массы.

τ₀ = c + σ × tg φ, (7.9)

где c - постоянное сцепление, зависящее от влажности; (σ × tgφ) - сцепление, обусловленное зацеплением частиц при уплотнении сыпучего материала.

Начальное сопротивление сдвигу и коэффициент внутреннего трения играют большую роль в процессе выпуска, определяя под­вижность обрушенной руды и ее сыпучие свойства. Значения этих величин во многом определяются степенью разрыхления шихтовых материалов или их плотностью. Последняя оказывает существенное влияние и на другие физико-механические свойства сыпучих материалов, например на объемный вес, угол естественного откоса как в покое, так и в движении.

Между величиной плотности укладки и коэффициентом внут­реннего трения шихтовых материалов существует взаимосвязь. По мере увеличения плотности шихтовых материалов и уменьшения коэффициента разрыхления сила сцепления возрастают. Это со­ответствующим образом отра­жается на ухудшении сыпучих свойств, особенно на первых этапах выпуска.

Углом естественного отко­са называют угол, образуемый линией свободно стоящего от­коса сыпучего материала с горизон­том.

Угол естественного откоса так же, как и другие физико-меха­нические свойства обрушенной руды, зависит от ее плотности, коэффициента внутреннего трения фракционного состава и других факторов. С увеличением плотности угол естественного откоса возрастает.

Зависимость угла естественного откоса от гранулометрического состава руды по­казана на рис. 7.1.

 

0 20 40 60 80 100