Турбулентные касательные напряжения

При достижении числом Рейнольдса критического значения на контактной поверхности потока с руслом непрерывно зарождаются турбулентные возмущения в виде вихрей различного размера и различной частоты. Эти вихри отрываются от стенок русла и пронизывают толщу поступательного потока, нарушая существующее до того упорядоченное (послойное) движение, вызывая в нем интенсивное турбулентное перемешивание. Распределение скоростей по сечению потока при турбулентном режиме движения представлено на рис. 3.3.

 

 

Рис.3.3. Распределение скоростей при турбулентном движении жидкости

в трубах: 1– вязкий подслой; 2 – ядро потока

 

Природа касательных напряжений, возникающих в турбулентном потоке более сложна, чем в ламинарном.

Сопротивление движению при ламинарном течении возрас­тает прямо пропорционально росту скорости. Эту зави­симость можно изобразить прямой линией с наклоном 45° в линейном и в логарифмическом масштабах осей коорди­нат (рис. 3.4).

 

	Рис. 3.4. Зависимость перепада давления от скорости при ламинарном (1) и турбулентном (2) течениях

 

Когда развивается турбулентность, то наблюдается сначала резкий скачок сопротивления, а затем с ростом скорости сопротивление растет быстрее, чем для ламинар­ного течения. Скачок может достигать 100 % и более. По­следующий рост сопротивления соответствует зависимости

, где n ~ 2,(3.19)

так как d(p+g ∙ h)/dZ (ось Z совпадает с осью трубы, u – средняя скорость по сечению трубы) пропорцио­нально касательному напряжению, оказывающему сопро­тивление движению, то становится очевидным, что при равных расходах t_тур > t_лам.

Один из первых исследователей турбулентности Ж. Буссинек объясняя явление увеличения касательных напряжений, ввел понятие турбулентной («вихревой») вяз­кости. Он написал для простого двухмерного случая

,(3.20)

где u – средняя местная скорость; h – динамическая молекулярная вязкость (свойство жидкости); h_Т – некоторая динамическая турбулентная («вихревая») вязкость, зависящая от состояния турбулентного движения. Слагаемое h . (du / dY) выражает вязкое напряжение, вычисленное по градиенту скорости усредненного движения. Слагаемое h_Т × (du / dY) выражает дополнительное напряжение, связанное с турбулентностью. Для ламинарного течения турбулентная вязкость равна нулю. Для турбулентного течения h_Т становится намного больше, чем молекулярная вязкость. Кроме того, величина h_Т переменна по пространству, занятому текущей жидкостью, так как она зависит от состояния течения, в то время как h является свойством только самой жидкости. Подобно динамической молеку­лярной вязкости динамическая вихревая вязкость имеет размерность Па∙с или кг/(м∙с).

 

4. ПОТЕРИ ЭНЕРГИИ ПРИ ДВИЖЕНИИ ЖИДКОСТИ И ГАЗОВ

 

При движении реальных жидкостей и газов по трубам, ка­налам, элементам металлургических печей, элементам оборудования, обслуживающим печи и т. п., вследствие трения или по другим причинам, некоторая часть механической энер­гии потока необратимо превращается в теплоту. Другими словами, наблюдается диссипация энергии, в результате чего уменьшается полное давление движущейся среды, при этом часть тепловой энергии рассеивается в окружающем пространстве, а часть остается в потоке, изменяя его внут­реннюю энергию. Эта безвозвратно потерянная часть полного давления для какого-либо участка системы характе­ризует гидравлические потери или гидравлическое сопро­тивление. В общем случае потери энергии при движении жидкости и газа рассчитываются по формуле

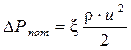,(4.1)

в которой коэффициент x, является коэффициентом гидрав­лического сопротивления. По своему физическому смыслу x – коэффициент пропорциональности между кинетической энергией потока и потерянной энергией. Поэтому его определяют как - отношение потерянной энергии к кинети­ческой, т. е.

.(4.2)

Обычно кинетическую энергию потока, оцениваемую ско­ростным (динамическим) давлением, определяют по средней расчетной скорости в сечении до гидравлического сопро­тивления. Из этого правила исключаются случаи движения жидкости и газа при внезапном сужении потока (вход воздуха в всасывающий патрубок вентилятора из атмосферы и т. п.); для них выбирают сечение после гидравлического сопротивления. В редких случаях коэффициенты гидравли­ческого сопротивления могут быть найдены теоретическим путем; обычно они определяются экспериментально. Коэф­фициент x всегда положителен. Значение x > 1,0 не должно вызывать удивления, так как израсходованная на преодо­ление сил сопротивления кинетическая энергия восстанавливается за счет потенциальной (статического давления), особенно четко это наблюдается при u = const.

Однако в реальных условиях встречаются участки, для которых в силу условного расчета ∆Р_пот приобретает отрицательное значение. По определению ∆Р_пот представляет собой раз­ность полных давлений на данном участке между сечения­ми 1 и 2, т. е.

∆Р_пот = Р_полн1 - Р_полн2 = (Р_ст1 + Р_дин1) – (Р_ст2 – Р_дин2 ).(4.3)

Из анализа этого выражения следует, что ∆Р_пот < 0 может быть тогда, когда на данном участке появляются дополни­тельные, внешние силы по отношению к данному потоку. Такого рода явления наблюдаются в ответвленном потоке, для которого при определенных углах отбора и соотноше­ниях скоростей основного и ответвленного потоков величи­на x может достигать 2,0.

Потери энергии при движении жидкости и газа обычно подразделяются на потери на трение, потери на местные сопротивления - в виде сужающих и расширяющих уст­ройств, поворотов, слияний и разделений потоков, задвижек, клапанов и т. п. Энергия потока в некоторых случаях мо­жет также расходоваться на преодоление действия геомет­рического давления.

 

4.1. Потери энергии на трение

 

Физическая сущность потерь давления на трение при ла­минарном и турбулентном режимах течения рассмотрена ранее. Для их расчета используется формула, в ко­торой величина гидравлического сопротивления для случая потерь на трение x зависит от длины трубопровода L, его гидравлического диаметра D и коэффициента трения λ, т. е.

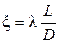.(4.4)

Введение понятия гидравлического диаметра позволяет использовать приведенное выражение для каналов и труб любого сечения - круглого, квадратного, треугольного, кольцевого и пр. Учет формы сечения трубопровода произ­водится расчетом по формуле

,(4.5)

где S – площадь сечения канала, П – его смоченный периметр.

Для круг­лых труб гидравлический диаметр совпадает с геометриче­ским. Трубы квадратного сечения имеют D, равный стороне квадрата. Гидравлический диаметр трубы кольцевого се­чения зависит от значений наружного D₁ и внутреннего D₂ диаметров кольца. Для трубопровода такой формы D = (D₁ -D₂).

Главная сложность расчета потерь на трение связана с выбором λ. В общем случае коэффициент трения определятся по величине числа Рейнольдса и шероховатости стенок трубопровода ∆. Последняя может быть идеальной и технической. В обоих случаях она оценивается отношением высоты бугорков d к диаметру трубопровода D. При иде­альной шероховатости высоты всех бугорков одинаковы и по длине трубопровода и по его периметру. Для реальных труб и закрытых каналов подобное условие не соблюдает­ся. Трубы с нулевой шероховатостью можно назвать глад­кими. Для круглых труб и ламинарного режима (Re < 2300)

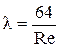.(4.6)

Эта формула, носящая имя Пуазейля, предполагает строго параболическое распределение скоростей. Ее теоре­тический вывод хорошо согласуется с экспериментом. Для этого и других случаев может быть использована более общая формула

,(4.7)

в которой коэффициенты ψ и k₁ характеризуют форму по­тока и особенности поля скоростей. Для круглых труб и переходного режима (Re ≤ l0⁵) применима формула Блазиуса

λ = 0,316 × Re^-0,25.(4.8)

Для таких же труб в турбулентном режиме (Re ≥ l0⁵) используется формула Никурадзе

λ = 0,0032 + 0,221 × Re^-0,237.(4.9)

Формулы справедливы для стабилизи­рованного потока. Им присвоены соответственно имена Пуазейля, Блазиуса и Никурадзе в честь заслуг этих ученых в развитии соответствующих разделов гидрогазодинамики. Указанные формулы дают представление о мини­мально возможных коэффициентах трения. Для труб с идеальной шероховатостью сведения о зна­чениях коэффициента трения можно получить из анализа опытных данных, приведенных на рис.4.1, известном как диаграмма Никурадзе.

 

 

 

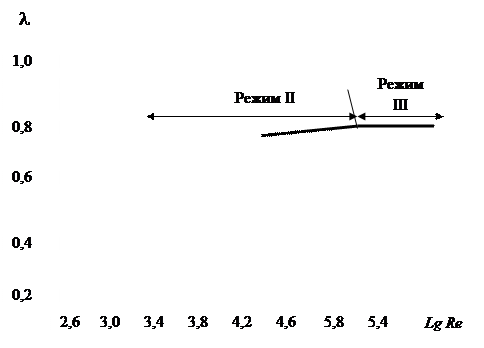
Рис.4.1.Зависимость коэффициента трения от характеристик режи­ма движения

и шероховатости для труб с идеальной шероховато­стью

 

Прежде всего, следует подчеркнуть, что в области ламинарного режима шероховатые трубы ве­дут себя как гладкие, так как срывов, завихрений при дви­жении потока не происходит из-за значительного влияния сил вязкости. Для них, λ = f₁(Re). Для II режима (переход­ного) величина коэффициента трения зависит от числа Re и от значения относительной шероховатости, т. е. λ = f₂(Re, Δ). Объяснение приведенных на рисунке зависимостей мо­жет быть получено из сопоставления высот бугорков шеро­ховатости и толщины пограничного слоя. Пока d_сл > d ше­роховатые трубы становятся подобными гладким, с ростом Re уменьшается толщина пограничного слоя, вершины бу­горков обнажаются, при этом создаются условия дополнительного образования вихрей. Чем выше бугорки, тем рань­ше происходит отрыв экспериментальной кривой от линии Блазиуса. Для турбулентного режима (III) коэффициент трения определя­ется только значением относительной шероховатости, т.е. он не зависит от числа Рейнольдса –λ = f₃(Δ). Такая зави­симость возможна при высокой турбулентности потока, когда дополнительное вихреобразование у бугорков прак­тически не меняет уровня турбулентности.

Потери на трение в области ламинарного режима пропорциональны скорости в первой степени, а в области развитого турбу­лентного режима, автомодельного – пропорциональны квадрату скорости. Поэтому этот режим (III) получил название квадратичного. Значения коэффициентов трения для труб с неравномер­ной шероховатостью могут быть найдены только по экспе­риментальным данным, обработанным по типу диаграммы Никурадзе.

В металлургической практике движение газов по тру­бам может происходить в условиях изменения температуры газов и давления. Все это влияет на величину потерь на трение между двумя рассматриваемыми сечениями. В пер­вом приближении учесть влияние этих факторов можно, допустив, что и температура, и давление по трубопроводу или его отдельному участку меняются линейно. С помощью уравнения Менделеева–Клапейрона можно получить соот­ношения для вычисления скорости потока u_PТ и плотности газа r_РТ для любых средних температур и давлений:

;(4.10)

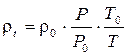_. (4.11)

Здесь индекс ноль указы­вает на то, что соответствующие величины должны быть определены при нормальных условиях. Подстановка этих соотношений в расчетную формулу дает

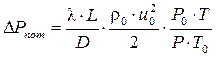,(4.12)

из анализа этой формулы следует, что при транспорте газа под повышенным давлением потери на трение уменьшаются. Этим выводом пользуются при организации дальнего га­зоснабжения. При значительных потерях энергии на трение, напри­мер, при подаче воздуха или пара для распыливания жидкого топлива в форсунках высокого давления среднее дав­ление в трубопроводе будет

,(4.13)

где Р_ст1 и Р_ст2 характеризуют давление газа в начале и в конце тру­бопровода или его участке. Очевидно, что в условиях движения газа под повышен­ным давлением доля динамического давления по отноше­нию к полному составляет незначительную величину ко­торой можно пренебречь. Тогда можно принять, что величина потерь на трение

.(4.14)

Используя результаты расчетов по этим формулам, нахо­дят либо начальное, либо конечное давление газа, которое обеспечивало бы нормальную работу соответствующих устройств. Для расчета потерь на трение первоначально опреде­ляют принадлежность к режиму течения (число Re), и, если требуется, то характеристики шероховатости и, затем по графикам отыскивают коэффициент тре­ния, величину которого и используют в оценке DP_тр по соответствующим формулам.

 

4.2. Потери энергии на местные сопротивления

 

Потери энергии на местные сопротивления обусловлены влиянием одного или нескольких одновременно действую­щих факторов: изменением скорости движения потоков, изменением формы и размеров сечения канала по пути дви­жения потока; изменением направления движения потока. Под их влиянием поток теряет свою механическую энер­гию при ускорении или замедлении движения. Энергия в значительных количествах также теряется в результате отрыва потока от ограничивающих его стенок и возникаю­щих при этом устойчивых вторичных течений. Конечно, на местных сопротивлениях некоторое количество энергии те­ряется за счет трения потока о стенки, однако в общем ба­лансе потерянной энергии доля этих потерь незначитель­на. Ее обычно не рассчитывают, так как при эксперимен­тальном определении коэффициентов местных сопротивле­ний учитывают и потери на трение.

Расчет потерь энергии на местные сопротивления про­изводят по формуле (4.1) с учетом тех особенностей опре­деления (ρ × u²), которые были отмечены в начале данной главы.

Рассмотрим некоторые наиболее характерные виды ме­стных сопротивлений.