МЕХАНИКА ЖИДКОСТЕЙ, ГАЗОВ

Федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Уральский федеральный университет имени первого

Президента России Б.Н.Ельцина»

 

С. А. Загайнов, Е. Ю. Лозовая

 

 

МЕХАНИКА ЖИДКОСТЕЙ, ГАЗОВ

И СЫПУЧИХ СРЕД

  Учебное пособие  

Участки а-а’ и b-b’ – новые. Здесь равновесие между объемом и поверхностью не установилось и на них мало поверхностно-активных веществ. Участка а’-с и b’-d старые, на них установилось равновесие между объемом и поверхностью и эти участки уже заполнены поверхностно-активными веществами. Поэтому происходит диффузия поверхностно-активных веществ от старых участков к новым. Этому процессу соответствует обратный поток – вытекание шлака. Диффузия ПВ препятствует потоку вытекания шлака между сближающимися пузырями, т.е. мешает их слиянию и оседанию пены. Этот эффект и называется кинетическим.

3. Количество поверхностно-активных веществ Na₂O, CaF₂, P₂O₅. Чем больше поверхностно-активных веществ, тем выше стабилизация пены.

Рост содержания Р₂О₅ в шлаке способствует повышению устойчивости пены. Это характерно для шлаков с малой основностью (СаО / SiО₂ » 0,55) и вязкостью. При повышении основности пена оседает.

Влияние содержания Na₂O и CaF₂ на устойчивость пены не однозначно. Для маловязких шлаков CaF₂ и Na₂O способствуют стабилизации пены, для высоковязких шлаков – способствуют оседанию пены.

4. Компоненты, повышающие поверхностную вязкость шлаков (MgO). Оксиды магния влияют на упрочнение адсорбционного слоя и стабилизируют пену.

5. Твердые частицы, попавшие между пузырями.

 

1.8. Коалесценция и коагуляция диспергированных частиц

 

В значительной части металлургических расплавов поверхностное натяжение (s) превышает не только десятки, но и сотни Дж/м². Такие системы термодинамически не устойчивы и способны к самопроизвольному укрупнению, которое может протекать: 1) путем исчезновения поверхности раздела между частицами – это явление называется коалесценция; 2) соединение частиц с сохранением поверхности раздела, например, для несмешивающихся жидкостей или для твердой фазы и жидкости, это явление называется коагуляция.

В ряде дисперсных систем процесс укрупнения протекает довольно медленно, что вызвано действием следующих стабилизирующих факторов:

- более высокая вязкость и механическая прочность адсорбционных слоев (по сравнению с объемом), наблюдается в шлаках содержащих много Fe₂O₃ или SiO₂, повышение вязкости адсорбционного слоя в этом случае связано с образованием соединений с магнием (MgFe₂O₄ или MgSiO₃);

- адсорбирование на поверхности полярных молекул какого-либо вещества, тогда под действием одноименных зарядов частицы будут отталкиваться;

- возникновение противотока в поверхностных слоях сближающихся частиц;

- присутствие на поверхности сближающихся частиц пузырьков газа, капелек или мелких твердых частиц оказывает блокирующее действие, препятствующее их объединению. И чем мельче частицы, тем выше эффект стабилизации.

Различают перекинетическую и ортокинетическую коагуляцию. Первая связана с укрупнением дисперсных систем под действием сил, симметрично расположенных по всем направлениям (силы вызваны броуновским движением). Вероятность столкновения частиц по всем направлениям одинакова.

Ортокинетическая коагуляция происходит под действием сил, имеющих преимущественное направление, по которому самая высокая частота столкновений. При определенных условиях возникают направления, по которым частота встреч оказывается наибольшей. Причинами могут быть различные размеры и форма частиц, наличие конвективных токов и т.п.

Наиболее сильное влияние оказывает наличие конвективных токов, при этом большое количество крупных частиц сильно ускоряет процесс коагуляции. Следовательно, наиболее действенными способами очистки стали от неметаллических включений являются создание в ней грубой взвеси и последующее перемешивание.

 

1.9. Флотация дисперсной фазы

(или условия плавания на поверхности жидкой фазы кусочков твердых

веществ)

Вопросы, касающиеся условий, при которых кусочки твердых материалов с большей плотностью по сравнению с жидкостью, плавают на поверхности, имеют значение в процессах обогащения руд и анализа металлургических процессов.

Если кусочек твердого тела (в форме архимедова цилиндра) в вертикальном положении поместить на поверхность жидкости (рис. 1.5), то в зависимости от его массы (m), величины архимедовой силы (А), поверхностного натяжения (s) и краевого угла смачивания (q) он либо затонет, либо будет плавать, в какой-то степени погрузившись в жидкость.

На рис. 1.5. показана схема действия сил на цилиндр в двух вариантах: при плохом (а) и хорошем (б) смачивании. Для обоих вариантов равнодействующая сила определяется по формуле

F = G – A + П × s × Cosq, (1.29)

где П – периметр цилиндра, м.

 

 

Рис. 1.5. Схема действия сил на цилиндр при плохом (а) и хорошем (б) смачивании

Цилиндр будет находиться в равновесии, если F = 0; если F > 0, то цилиндр погрузится в жидкость; если F < 0, то всплывет.

Тело с большей плотностью, чем у жидкости, может плавать на поверхности лишь в условиях плохого смачивания, когда Cosq < 0.

Явления, характерные для флотации, имеют место при кипении стали в сталеплавильной печи: пузырьки газа {CO} переходят в шлак в металлической оболочке, после разрыва, которой превращается в каплю, тонущую в шлаке.

Если в капле металла имеется растворенный [C], а в шлаке присутствует закись железа (FeO), то окисление углерода вызовет зарождение на капле пузырьков {CO}. По мере роста пузырька капля вновь всплывает на поверхность, где пузырек разрывается и капля опускается вниз. Такое явление появляется до тех пор, пока из капли не удаляется углерод.

В шлаке может находиться до 5 % металла (по отношению к массе шлака) в виде корольков при обычной мартеновской плавке и до 30 % в условиях продувки жидкого металла кислородом. Так как их удельная поверхность велика по сравнению с поверхностью контактирующих слоев металла и шлака, то удаление примесей ускоряется. В тоже время это явление может привести к заметным потерям металла со шлаком.

 

1.10. Влияние поверхностного натяжения и явления смачивания

на кристаллизацию стали

 

Процесс кристаллизации стали складывается из двух стадий - зарождения кристаллов и последующего их роста. Различают гомогенное и гетерогенное зарождение кристаллов. Под гомогенным подразумевают образование зародышей кристалла в объеме жидкой фазы, под гетерогенным – на уже имеющейся межфазной поверхности.

Рассмотрим процесс кристаллизации. При охлаждении жидкого металла в изложнице или кристаллизаторе в какой-то момент времени его температура становится равной температуре равновесия твердой и жидкой фаз Т_кр (кристаллизации) и начинается кристаллизация с образования зародышей новой фазы.

При кристаллизации, т.е. образовании зародыша новой фазы, наблюдается две тенденции: фазовый переход уменьшает свободную энергию системы (потенциал Гиббса, DG_V), но в то же время появление зародыша кристалла, а соответственно новой поверхности, увеличивает её (DG_S).

Таким образом, в конечном итоге увеличение размера зарождающегося кристалла вначале сопровождается возрастанием DG, а затем снижением (рис. 1.6).

		Рис. 1.6. Изменение свободной энергии системы: DGS – при образовании новой поверхности; DGV – уменьшении объема; DGХ – суммарное изменение свободной энергии

 

 

 

 

Радиус кристалла, для которого DG имеет максимальное значение называется критическим (r_кр). Таким образом, критический - это такой размер, начиная с которого дальнейший рост сопровождается снижением суммарной свободной энергии образования зародыша. Зародыши радиусом r > r_кр будут расти, если же r < r_кр, могут только исчезать, так как условий для их роста нет.

Величину критического радиуса зародыша определяют из соотношения

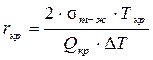,(1.30)

где s_{т - ж} – межфазное натяжение на границе жидкой и твердой фаз, Дж/м²; Т_кр – температура начала кристаллизации, К; DТ – величина переохлаждения, К; Q_кр – скрытая теплота кристаллизации, Дж/кг.

Сравним форму зародыша, образовавшегося на поверхности твердой фазы (рис. 1.7 а) с зародышем, возникшим в объеме фазы (рис. 1.7.б).

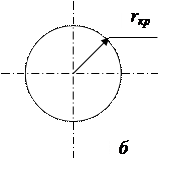Рис. 1.7. Схемы формирования зародышей, образовавшихся на поверхности твердого тела (а) и в объеме жидкой фазы (б)

 

Наличие твердой поверхности облегчает процесс образования зародышей при хорошем смачивании, так как из уравнения (1.24) следует

s_т-ж = s_т – s_ж · Соsq .(1.31)

В случае абсолютного смачивания q = 0, Соsq = 1, следовательно s_т-ж стремится к минимуму и размер r_кр (радиус зародыша) будет иметь минимальное значение, что способствует легкому образованию зерен.

В случае полного не смачивания q = p, Соsq = – 1,s_т-ж = s_т + s_ж , т. е. имеет максимальное значение и радиус зародыша кристалла критический (r_кр) будет иметь очень большое значение, следовательно зародыши не образуются.

Таким образом, готовые поверхности раздела фаз в системе (стенки кристаллизатора, изложницы, неметаллические включения) существенно облегчают зарождение твердой фазы.

 

2. РАВНОВЕСИЕ ЖИДКОСТИ И ГАЗА

 

 

Равновесие жидкости и газа возникает в тех случаях, когда жидкость либо находится в состоянии покоя, либо когда весь объем жидкости перемещается с одинаковой скоростью подобно твердому телу. Равновесие является результатом действия сил тяжести и связей на границе раздела жидкости и газа.

2.1. Понятие напряженного состояния жидкости

 

Когда жидкость подвергается воздействию внешних сил, в ее объеме возникают внутренние напряжения.

Предположим, что в массе жидкости под влиянием внешних сил возникают соответствующие внутренние силы (рис. 2.1). Проведем мысленно внутри рассматриваемой жидкости поверхность, разделяющую ее объем на две части I и II. Отбросим одну из них, например I; чтобы часть II осталась в равновесии во всех точках разделяющей поверхности нужно ввести такие же силы, с которыми масса I действовала на массу II. На элементарной площади Dw, разделяю -

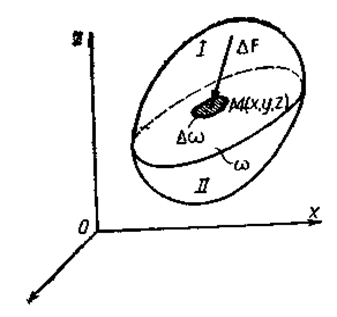Рис. 2.1. К определению напряжения в точке

щей поверхности действует сила DF. Площадь Dw может быть стянута в точку М с координатами X, Y, Z. В этом случае как площадь поверхности Dw, так и сила DF стремятся к нулю. Предел отношения силы DF к площади поверхности Dw называется напряжением в точке с координатами X, Y, Z. . (2.1)

Здесь w − поверхность раздела. Сила DF, в общем случае, будет направлена под углом к поверхности раздела, имея, таким образом, как нормальную, так и касательную составляющие. Значения последних, приходящихся на единицу площади поверхности, называют нормальными и касательными напряжениями.

Составляющие напряжений, направленные перпендикулярно грани, называются нормальными напряжениями. Составляющие, находящиеся в плоскости граней, называются касательными напряжениями.

Касательные напряжения возникают тогда, когда имеются внутренние градиенты скорости. В состоянии равновесия касательные напряжения равны нулю и напряженное состояние определяется совокупным действием нормальных напряжений, равных между собой.

2.2. Гидростатическое давление и его свойства

 

Давлением называется сила, действующая на единицу поверхности жидкости. Давление измеряется в Па ().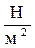

Величина, равная модулю напряжения (s), в гидромеханике называется гидростатическим давлением в точке и определяется по формуле

Р = ês ê. (2.2)

Гидростатическое давление обладает двумя свойствами.

Первое свойство: Сила гидростатического давления направлена по внутренней нормали (не оказывает сопротивление растягивающим усилиям) к поверхности, которая воспринимает это давление и определяется по уравнению

Р = r × g × h. (2.3)

Второе свойство: Величина гидростатического давления не зависит от угла наклона площадки.

 

2.3. Дифференциальное уравнение равновесия жидкости

(уравнение Эйлера)

 

Хотя величина нормального напряжения, а следовательно, и давления при равновесии не зависит от ориентации площади действия, в различных точках жидкости, в общем случае, она может быть различной. Иными словами, давление, или как еще называют, гидростатическое давление, есть функция координат, т.е. Р = f (X, Y, Z).

Расположим внутри покоящейся жидкости около произвольной точки О прямоугольную систему координат так, чтобы ось ОZ получила направление вертикально вверх. Выделим в жидкости элемент в форме параллелепипеда с ребрами dx, dy, dz, параллельными осями координат, и напишем условия его равновесия под действием шести сил давления на его грани и равнодействующей объемных (массовых) сил Q (рис. 2.2).

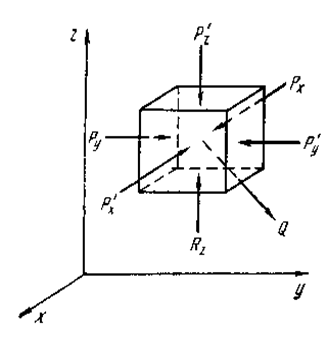Рис. 2.2. Равновесие под действием сил давления на грани параллелепипеда и равнодействующих объемных (массовых) сил

Уравнения равновесия выделенного объема имеют вид: SFx = 0; SFy = 0; SFz = 0. В уравнение SFy = 0 войдут следующие силы SFy = Py - P'y + Qy, где Ру – сила давления на левую грань; P'y – сила давления на правую грань; Qy – проекция объемной силы Q на ось Оy. Py = P ∙ dx ∙ dz, P'y = P' ∙dx ∙ dz; и Qy = Y ∙ r ∙ dx ∙ dy ∙ dz, где Р – гидростатическое давление среднее для левой грани, Па; P' – гидростатическое дав -

ление среднее для правой грани, Па; r – плотность жидкости, кг/м³; Y – проекция на ось ОУ ускорения, соответствующего силе Q_y, м/с².

Выделенный объем достаточно мал. Это позволяет считать, что давление внутри него по любой координате изменяется линейно.

Тогда, разлагая Р¢ вблизи у = 0 в ряд Тейлора и ограничиваясь линейными слагаемыми ряда, получим Р¢_y = Р + 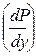∙ dу.

SF_y = P ∙ dx ∙ dz – [P +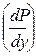∙ dy] ∙ dx ∙ dz + Y ∙ r ∙ dx ∙ dy ∙ dz = 0

или после преобразований и деления на dx ∙ dy ∙ dz

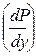–+ r ∙Y = 0.

Получив по аналогии два других уравнения, будем иметь следующую систему уравнений Эйлера:

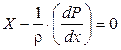
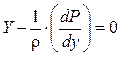(2.4)

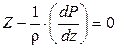
Умножим каждое уравнение на dx, dy и dz соответственно, сложим их и получим уравнение

dP = r ∙ (X ∙ dx + Y ∙ dy + Z ∙ dz). (2.5)

Это уравнение называется основным дифференциальным уравнением равновесия жидкости.

Поверхность, во всех точках которой давление постоянно Р = const, называется поверхностью уровня и в любой ее точке dP = 0и следовательно

X ∙ dx + Y ∙ dy + Z ∙ dz = 0. (2.6)

Это и есть уравнение поверхности уровня. Поверхность уровня обладает двумя основными свойствами:

1. Поверхности уровня не пересекаются между собой;

2. Внешние массовые силы направлены по внутренней нормали к поверхности уровня.

 

2.4. Распределение давления в покоящейся жидкости

 

 

В рассматриваемом случае массовой силой является сила тяжести, ускорением - ускорение свободного падения (g),поэтому в выбранной системе координат проекции единичной массовой силы на оси ОX, ОY и ОZ будут: X = 0, Y = 0, Z = -g. Воспользуемся основным дифференциальным уравнением равновесия жидкости (2.5) и после подстановки в него X = 0, Y = 0 и Z = –g получим

dP = –r ∙ g ∙ dZ. (2.7)

После интегрирования и деления на (r ∙ g) получим

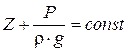. (2.8)

Это основное уравнение гидростатики, оно выражает закон распределения гидростатического давления в покоящейся жидкости.

Для определения постоянной интегрирования рассмотрим равновесие жидкости в сосуде произвольной формы со свободной поверхностью (рис. 2.3).

 

 

Рис. 2.3. Равновесие жидкости в поле силы тяжести

 

Давление в каждой точке на свободной поверхности Р = Р₀, расстояние от произвольной плоскости сравнения (в нашем случае – плоскость ХОУ)до свободной поверхности равно Z₀. Тогда const = Z₀ +, и основное уравнение приобретает следующий вид:

, (2.9)

или

P = P₀ + r ∙ g ∙ (Z₀ – Z). (2.10)

Нетрудно заметить, что разность отметок Z₀ – Z = h представляет собой глубину погружения точки М, поэтому

P = P₀ + r ∙ g ∙ h. (2.11)

Это другая форма основного уравнения гидростатики, удобная для практических расчетов.

В гидравлике величина Р называется полным или абсолютным гидростатическим давлением. Первое слагаемое уравнения (2.11) Р₀ принято называть внешним давлением или давлением на поверхности. Его величина остается постоянной для любой точки внутри покоящейся жидкости.

Величина второго слагаемого из уравнения (2.11), зависит при постоянной плотности жидкости (r) только от глубины погружения рассматриваемой точки. Эта величина называется в гидравлике избыточным давлением. Таким образом, уравнение (2.11) можно представить в виде

P_полн = P₀ + Р_изб. (2.12)

Из уравнения (2.12) следует, что распределение гидростатического давления по вертикали линейно зависит от глубины погружения рассматриваемой точки и может быть представлено в виде трапеции (рис. 2.4 а) для полного давления или прямоугольного треугольника для избыточного давления (рис.2.4 б). Отметим, что котангенс угла наклона линии давления АВ прямо пропорционален плотности жидкости.

 

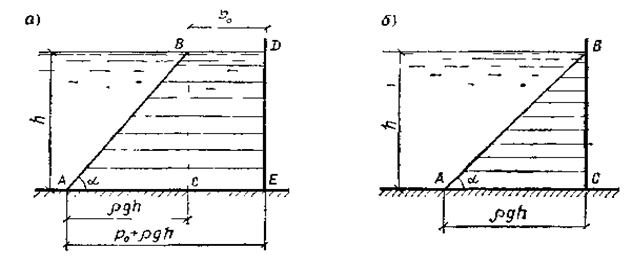
Рис. 2.4. Распределение гидростатического давления

а - полного; б - избыточного.

2.5. Равновесие несмешивающихся жидкостей

 

Рассмотрим равновесие трех несмешивающихся жидкостей, заполняющих сосуд произвольной формы (рис. 2.5).

Очевидно, что жидкости должны расположиться в сосуде в соответствии с их плотностями: жидкость с меньшей плотностью всегда располагается выше жидкости с большей плотностью. Такое расположение жидкостей определяется общим законом механики для любых тел в поле силы тяжести.

 

Рис. 2.5. Равновесие несмешивающихся жидкостей.

 

 

Поверхность уровня при равновесии несмешивающихся жидкостей в поле силы тяжести представляет собой семейство горизонтальных плоскостей.

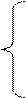Распределение давления, как это следует из основного уравнения гидростатики (2.11), линейно зависит от глубины погружения точки. Особенность в распределении давления заключается в том, что на границе раздела жидкостей угол наклона линии давления меняется в соответствии с изменением плотности жидкости при переходе от слоя к слою. Очевидно, для границ раздела справедливы следующие равенства:

P₁ = P₀ + r₁ ∙ g ∙ h₁ ;

P₂ = P₁ + r₂ ∙ g ∙ h₂ ; (2.14)

P₃ = P₂ + r₃ ∙g ∙ h₃ .

2.6. Движение резервуара с жидкостью с постоянным ускорением (а)

 

Относительным равновесием жидкости называется такое состояние, при котором каждая ее частица сохраняет свое положение относительно твердой стенки движущегося сосуда. При относительном равновесии рассматриваются две задачи: определяется форма поверхности уровня и выясняется характер распределения давления. Очевидно, в этом случае следует учитывать силы инерции, дополняющие систему массовых сил, действующих в жидкости, находящейся в состоянии абсолютного покоя.

В общем случае любое сложное движение сосуда с жидкостью можно представить в виде суммы трех простейших движений: поступательного по вертикали и горизонтали и вращательного.

Рассмотрим поступательные движения сосуда с жидкостью по вертикали и горизонтали:

1. Движение резервуара с жидкостью по вертикали, с постоянным ускорением а (рис. 2.6). Для определения уравнения поверхности уровня воспользуемся уравнением (2.6).

 

 

 

Рис. 2.6. Вертикальное перемещение резервуара с жидкостью

 

 

Проекции единичных массовых сил на координатные оси будут: Х = 0; У = 0; Z = - g ± a. Знак "-" соответствует равноускоренному подъему резервуара; знак "+" - равноускоренному спуску. Составим уравнение поверхности уровня

(- g ± a) ∙ dZ = 0. (2.14)

Если а ¹ g, то dZ = 0 и, следовательно, Z = const. Последнее равенство означает, что при равноускоренном перемещении резервуара с жидкостью по вертикали поверхности равного давления представляют собой горизонтальные плоскости.

Характер распределения давления в рассматриваемом случае получим из основного уравнения равновесия жидкости (2.5), которое принимает форму

dР = r ∙ (- g ± a) ∙ dZ. (2.15)

Интегрируя, получим

P = r ∙ (- g ± a) ∙ Z + C, (2.16)

где С – постоянная интегрирования, определяемая из граничных условий Z = Z₀ и Р = Р₀.

После подстановки граничных условий получаем закон распределения давления вдоль любой вертикали

. (2.17)

2. Горизонтальное перемещение резервуара с жидкостью, с постоянным ускорением а (рис. 2.7).

 

Рис. 2.7. Горизонтальное перемещение резервуара с жидкостью

 

В этом случае X = - a, Z = -g. Подставим эти значения в уравнение (2.6), тогда поверхность равного давления определяется уравнением

- (a × dX + g × dZ) = 0. (2.18)

Поверхностями равного давления будут плоскости, углы наклона которых к горизонтальной плоскости определяются угловым коэффициентом, равным (-a /g).

Закон распределения давления можно получить после интегрирования уравнения (2.5) с учетом Х = -a, У = 0, Z = -g, а также граничных условий Х = Х₀, Z = Z₀, Р = Р₀ в следующем виде

P = P₀ + r ∙ a ∙ (X₀ − X) + r ∙ g ∙ (Z₀ – Z).(2.19)

Уравнение (2.19) показывает, что при движении резервуара с жидкостью вдоль горизонтальной плоскости с постоянным ускорением а распределение давления подчиняется линейному закону для любой фиксированной вертикали (Х = Х₁, Х = Х₂,…). Это уравнение также можно записать в форме основного уравнения гидростатики:

P = P₀¢ + r ∙ g ∙ (Z₀ – Z), (2.20)

где P₀¢ = P₀ + r ∙ а ∙ (Х₀ – Х).

 

2.7. Давление жидкости на плоскую поверхность

 

Действие сил гидростатического давления, распределенного по поверхности, которая это давление воспринимает, может быть заменено действием одной сосредоточенной силы - их равнодействующей.

При определении силового воздействия жидкости на твердую поверхность решают обычно две задачи: определяют величину равнодействующей сил гидростатического давления и находят точку ее приложения (центр давления).

Рассмотрим простейший случай – давление жидкости на плоское дно цилиндрического сосуда (рис. 2.8, а).

Выделим в пределах площади дна элементарную площадку dw; очевидно, что давление dР в каждой ее точке будет постоянным. Сила давления dР на эту площадку равна: dР = Р × dw(где Р = Р₀ + r ∙ g ∙ h – полное гидростатическое давление в любой точке дна).

	Рис. 2.8. Давление жидкости на горизонтальную плоскую поверхность

 

 

Равнодействующая силы давления, очевидно, определится интегралом от элементарной силы, взятым по всей площади дна

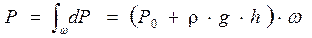,(2.21)

так как входящие под знак интеграла Р₀ и r, g – величины постоянные.

Уравнение (2.21) показывает, что независимо от формы сосуда, заполненного жидкостью, и формы его дна сила гидростатического давления будет одинакова при условии Р = Р₀ и h₁ = h₂ = h. В случае равномерной распределенной нагрузки на дно сосуда w точка приложения равнодействующей и центр тяжести площадки совпадают

2.8. Давление жидкости на криволинейные поверхности

(закон Архимеда)

Выберем внутри покоящейся жидкости произвольный объем W, ограниченный поверхностью S (рис. 2.9). Очевидно, поверхностные силы (в данном случае только силы гидростатического давления) будут направлены по внутренним нормалям к граничной поверхности.

 

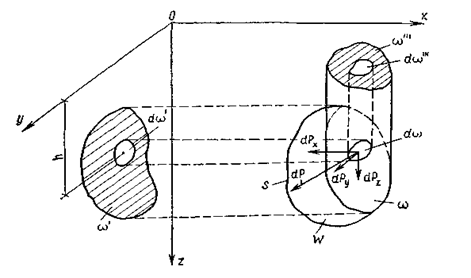
Рис. 2.9. Давление жидкости на криволинейную поверхность

 

Выделим в пределах поверхности S криволинейную площадку w. Так как площадка w находится в равновесии, система распределенных по ее поверхности сил dР может быть заменена одной равнодействующей Р с составляющими Р_x, P_y, P_z, параллельными соответствующим координатным осям OX, OY, OZ.

Сила dP, действующая на площадку dw определится по формуле

dP = (P₀ + r ∙ g ∙ h) ∙ dw, (2.22)

где h - глубина погружения центра тяжести площадки dw относительно свободной поверхности.

Так же как и равнодействующая Р, элементарная сила давления может быть представлена в виде

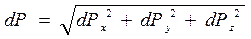, (2.23)

где dP_x, dP_y − горизонтальные составляющие силы dP, действующие вдоль осей, параллельных осям ОХ и ОУ; dP_z − вертикальная составляющая силы dP.

Определим каждую составляющую отдельно.

Рассмотрим сначала одну из горизонтальных составляющих, например dP_x. Очевидно dP_x = dP× cos (`dP, OX), где cos(dP, OX) - косинус угла между направлением вектора силы dP и осью ОХ.

После подстановки dP из уравнения (2.23) и интегрирования для горизонтальной составляющей можно записать

P_X = (P₀ + r ∙ g ∙ (X₀ − X)) ∙ w_X, (2.24)

где w_X – проекция площадки w на плоскость YOZ.

Уравнение для горизонтальной составляющей, действующей вдоль оси ОУ, легко записать по аналогии с выражением (2.25)

P_Y = (P₀ + r ∙ g ∙ (Y₀ - Y)) ∙ w_Y,(2.25)

где w_Y – проекция площадки w на координатную плоскость XOZ. P_Z = (P₀ + r ∙ g ∙ (Z₀ − Z)) ∙ w_Z,(2.26)

где (Z₀ – Z) ∙ w_Z = W_т.д. – называют телом давления и

P_Z = P₀ ∙ w_Z + r ∙ g ∙ W_т.д. (2.27)

Следовательно, вертикальная составляющая силы полного гидростатического давления на криволинейную поверхность равна сумме сил внешнего давления Р₀ на проекцию рассматриваемой площадки на свободную поверхность и силы, определяемой весом тела давления.

3. ОСНОВЫ КИНЕМАТИКИ И ДИНАМИКИ

ЖИДКОСТИ И ГАЗОВ

3.1. Понятие кинематики

 

Часть механики, в которой рассматривается движение жидкостей и газов без выяснения причин его возникновения называется кинематикой. В кинематике изучается положение частиц в пространстве (точка с координатами X,Y,Z) в зависимости от времени (t).

Точка – это место в пространстве; частица – малая часть материального континуума. Движение и течение (непрерывное движение) – это мгновенное или непрерывное изменение конфигурации сплошной среды.

 

3.2. Два метода описания движения сплошной среды

 

1. Метод Лагранжа – движение описывается радиусом вектором жидкой частицы r(t, a, b, c) или его проекциями на оси ОX, ОY, ОZ,причем за параметры a, b, c, принимаются значения X, Y, Z в начальный момент времени. Таким образом, в некоторый произвольный момент времени, условно принятый за нуль, задаются координаты каждой частицы a,b,c и после этого следят за движением этой частицы в потоке. Поэтому в описании Лангранжа координаты X, Y, Z всегда являются взаимосвязанными с начальными координатами a, b, c. Положение частицы в любой момент времени определяется системой уравнений вида:

X = f(t, a, b, c);

Y = f(t, a, b ,c); (3.1)

Z = f(t, a, b ,c).

Соответствующие скорости

;(3.2)

и ускорения

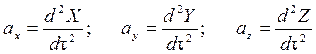.(3.3)

При этом необходимо сохранять постоянными начальные координаты a, b, c.

2. Метод ЭЙЛЕРА. Наблюдают за тем, что происходит в фиксированной области пространства по мере того как идет время. В данном методе выполняют описание скорости потока в различных точках, т.е. скоростей частиц, находящихся в текущий момент времени в разных точках пространства. Поэтому в описании Эйлера координаты X, Y, Z являются независимыми переменными. Если эти скорости не зависят от времени, то движение называется стационарным. Для стационарного движения:

u = u (r) , то u _x = f (X, Y, Z) ; u _y = f (X, Y, Z); u _z = f (X, Y, Z).

Если скорости зависят от времени, то движение нестационарное

u = u (t, r), то u _x = u _x (t, X, Y, Z) ; u _y = u _y (t, X, Y, Z); u _z = u _z (t, X, Y, Z).

Ускорение ,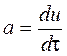

a _x = du_x / dt + u_x ∙ (du_x / dX) + u_y ∙ (du_x / dY) + u_z ∙ (du_x / dZ)

a _y = du_y / dt + u_х ∙ (du_y / dX) + u_y ∙ (du_y / dY) + u_z ∙ (d u_y / dZ) (3.4)

a _z = d u_z / dt + u_х ∙ (d u_z / dX) + u_y ∙ (d u_z / dY) + u_z ∙ (du_z / dZ)

3.3. Линии тока, трубки тока, траектории

 

Линией тока называется воображаемая линия, являющаяся геометрическим местом точек в пространстве, в которых векторы скорости в данный момент времени направлены по касательной к этой линии. Линии тока указывают направление движения в каждой точке вдоль этой линии.

Трубка тока или элементарная струйка – это воображаемый канал, заключенный между линиями тока. При стационарном движении линии тока остаются неподвижными по отношению к системе отсчета. При установившемся движении линии тока совпадают с траекториями частиц.

Траектории частиц удобно определять по скорости (уравнение 3.2), в случае плоского двумерного течения жидкости u _z = dz / dt = 0; u _x = dx / dt; u _y = dy / dt, отсюда следует

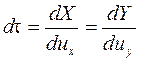. (3.5)

Между двумя линиями тока количество протекающей жидкости постоянно. Объемный расход в трубке тока DV = ½u_n × dS½,где u_n - нормаль к площади dS.

3.4. Уравнение неразрывности

 

Принцип сохранения массы жидкости для любой определенной системы: (Чистый приток массы в систему) = (Приращению массы системы).

Для случая одномерного движения, при котором параметры потока изменяются лишь вдоль какой-то одной координаты (например, ОХ) уравнение неразрывности записывается следующим образом

. (3.6)

В случае установившегося течения данное выражение упрощается, так какd(r × u) / dХ = 0. Интегрируя это соотношение от сечения потока 1 до сечения потока 2, получим

r₁ . u₁ .S₁ =r₂ . u₂ . S₂ = const, (3.7)

где S₁, S₂ – площади поперечного сечения 1 и 2 соответственно; u₁, u₂ – скорости потоков в сечениях 1 и 2.

Это уравнение неразрывности для трубки тока. Оно выполняется для движения жидкости в трубках и каналах. Для несжимаемых жидкостей при r = const это уравнение еще более упрощается, т.е.

u₁ . S₁ = u ₂ . S₂ = const.(3.8)

Форма уравнения неразрывности (3.8) показывает, что как массовый, так и объемный расходы постоянны, и если сечение трубопровода увеличивается, то средняя расходная скорость потока падает.

3.5. Уравнение баланса импульса

 

При записи уравнения баланса импульса (количества движения) следует выбирать систему, к которой применяют принцип сохранения этой величины. Система может иметь конечные размеры. Однако наиболее удобная форма для записи уравнений баланса импульса получается в том случае, когда в качестве такой системы выбирают малый объем. На элементарный объем DX, DY, DZ действуют нормальные s_Х и касательные t_XY напряжения, которые зависят от вязкости, плотности и давления. Для общего описания напряженного состояния тела требуется девять скалярных величин – три нормальных и шесть касательных напряжений.

Принцип сохранения импульса для элементарного объема может быть схематично записан в следующем виде:

(Чистый приток импульса в систему)

+ (Сумма всех поверхностных сил, действующих на систему)

+ (Сумма всех объемных сил, действующих на систему)

= (Скорости возрастания импульса)

или (Произведение массы тела на его ускорение)

= (Сумме всех сил, действующих на систему).

m ∙ (u ₂ - u ₁) = P + T + G + R,(3.9)

где u – скорость потока; P, T – нормальные и касательные силы, приложенные к элементарным площадкам; G – массовые силы; R – реакция твердых тел, если таковые имеются, с которыми соприкасается контрольная поверхность; индексы 1 и 2 обозначают начальный и конечный момент интервала времени Dt или левое и правое сечения контрольного объема.

3.6. Уравнение Навье–Стокса

 

Уравнение применяется для описания поведения жидкости, находящейся под действием сил тяжести. Для несжимаемой жидкости при изотермических условиях ее движения система уравнений имеет следующий вид:

du_x / dt + u_x ∙ (du_x / dX) + u_y ∙ (du_x / dY) + u_z ∙ (du_x / dZ) =

-g(dh / dX) - (1/r) ∙(dP / dX) + (h /r) ∙[d²u_x / dX² + d²u_x / dY² + d²u_x / dZ²]

du_y / dt + u_х ∙ (du_y / dX) + u_y ∙ (du_y / dY) + u_z ∙ (d u_y / dZ) =

-g(dh / dY) - (1/r) ∙(dP /dY) + (h /r) ∙[d²u_y / dX² + d²u_y / dY² + d²u_y / dZ²](3.10)

d u_z / dt + u_х ∙ (d u_z / dX) + u_y ∙ (d u_z / dY) + u_z ∙ (du_z / dZ) =

-g(dh / dZ) - (1/r) ∙(dP / dZ) + (h /r) ∙[d²u _z / dX² + d²u _z / dY² + d²u _z / dZ²]

где h – высота положения точки, отсчитываемая в вертикальном направлении.

Полученная система уравнений называется уравнениями Новье-Стокса. В этой системе уравнений 4 независимых переменных u _x, u _y, u _z и r. Совместное решение этой системы вместе с уравнением неразрывности (3.7) позволяет во многих случаях определять поля скоростей и давлений при движении жидкости. Эта система не имеет аналитического решения, интегрируется только для некоторых частных случаев. Однако с успехом используется, например, для изучения движения вязкой жидкости в пограничном слое и т.п.

3.7. Уравнение Бернулли

 

Уравнение Бернулли – частный случай решения уравнений движения жидкости (3.10) полученное при следующих допущениях:

1. Движение жидкости считается установившимся.

2. Распределение давления в сечениях, отстоящих друг от друга на расстоянии L, подчиняется гидростатическим законам.

3. Скорости в любой точке каждого сечения одинаковы.

4. Обмен теплом и механической энергией с внешней средой отсутствует.

Рассмотрим баланс энергии массы жидкости в произвольном канале между двумя сечениями. Энергия единицы массы или объема движущейся жидкости равна сумме механической и внутренней энергии. По закону сохранения энергии, суммарное количество энергии остается постоянным. При течении жидкости от одного сечения к другому происходит процесс необратимого превращения части механической энергии во внутреннюю (тепловую).

Работа сил вязкости, произведенная между двумя сечениями потока и отнесенная к единице массы движущейся жидкости, называется потерями механической энергии, или гидравлическими потерями.

Обозначим давление в выбранных сечениях потока Р₁ и Р₂; расстояние от центров тяжести этих сечений до произвольной плоскости сравнения (ОХУ) Z₁ и Z₂; скорости в них u₁ и u₂.

Тогда уравнение баланса механической энергии между двумя сечениями (уравнение Бернулли) запишется в следующем виде

.(3.11)

Здесь DP_пот – потери давления; индексы 1 и 2 обозначают левое и правое сечения контрольного объема.

При течении вязкой жидкости следует учитывать неравномерность распределения скоростей по сечению потока. В этом случае уравнение Бернулли принимает следующий вид

.(3.12)

Здесь, коэффициент (а) учитывает неравномерность распределения скоростей по сечению потока (при равномерном распределении а = 1, при параболическом распределении а = 2).

 

3.8. Понятие турбулентного и ламинарного режимов движения жидкостей

и газов

 

Различают два режима движения жидкостей и газов – ламинарный и турбулентный. Ламинарный режим движения жидкости характеризуется упорядоченным, слоистым движением частиц в трубках тока, при котором отдельные слои жидкости скользят относительно друг друга, не смешиваясь между собой. Состояние движения жидкости, называемое турбулентным или неупорядоченным, возникает когда частицы жидкости движутся по сложным, все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание (распад потока на отдельные вихри).

Одним из источников турбулентности являются поверхности разрыва скорости, то есть такие области, где имеется резкий скачек скорости между прилегающими слоями жидкости. При турбулентном движении направление скорости каждой частицы может не совпадать с направлением движения потока.

Опыты, проведенные Рейнольдсом показали, что переход потока от ламинарного к турбулентному движению происходит при определенных условиях, которые определяются численным значением так называемого числа Рейнольдса (Re).

, (3.13)

где u – скорость, м/с; D – определяющий размер, м; ρ – плотность жидкости, кг/м ³; h – коэффициент динамической вязкости, Па· с.

В числителе содержится сила инерции потока, а в знаменателе сила вязкого трения.

Число Рейнольдса, при котором происходит переход от ламинарного к турбулентному движению примерно равно 2000–2300 и называется критическим числом Рейнольдса (Re_кр). Проведенные исследования показывают, что критическое число Рейнольдса увеличивается в сужающихся трубках и уменьшается в расширяющихся. Ламинарный и турбулентный режимы отличаются не только характером движения частиц (на­личием поперечных скоростей при турбулентном движе­нии), но также особенностями распределения скоростей по сечению и характером зависимости между потерями напора и скоростью.

 

Ламинарное равномерное движение жидкости в трубах

     

Турбулентные касательные напряжения

     

Внезапное расширение

При выходе потока из канала малого диаметра в канал большего диаметра вдоль стенки расширяющегося участ­ка в силу различия скоростей на оси потока и…  

Диффузоры

С помощью этих устройств удается преобразовать ки­нетическую энергию потока в потенциальную. Для создания конического диффузора с минимальными…    

Внезапное сужение

 

Конфузоры

   

Потери давления на поворотах

Источником потерь давления на поворотах является сила, которая действует на любой элементарный объем , (4.26) где dm = r × j × r × dr. Давление, вызванное этой силой

Простые трубопроводы

ΔРΣ = ΣΔРтр + ΣΔРм.с. ± ΣΔРгеом. (4.31) При решении первой задачи все параметры трубопро­вода известны; задан и расход… Вторая задача, как правило, не имеет однозначного решения, так как коэффициенты ξ и λ являются функциями…

Определение скорости осаждения (всплывание) твердых частиц

, (6.3) где m -масса частицы с учетом присоединенной массы жидкости; (du / dt) -… Участок стабилизации скорости при свободном осаж­дении относительно мал, поэтому основной участок час­тица проходит…

Крупность руды, мм

Рис. 7.1. Зависимость угла естественного откоса от крупности руды.    

Зависимость эксцентриситета эллипсоида выпуска от его высоты

Опытами установлено, что эксцентриситет эллипсоидов выпуска при одном и том же сыпучем материале и постоянном радиусе выпускного отверстия… Зависимость объемов эллипсоидов выпуска от их высоты с достаточной точностью… , (8.5)

Влияние гранулометрического состава сыпучего материала и влажности на объем эллипсоида выпуска

В результате исследований было установлено следующее: 1. С увеличением (в некоторых пределах) размеров частиц сыпучего материала… 2. На величину объемов эллипсоидов выпуска влияет форма поверхности частиц. При окатанных зернах объем эллипсоида…

Влияние формы и размеров

Опыты показали, что с увеличением площади выпускного от­верстия независимо от его формы объем фигуры выпуска увели­чивается. При одинаковых площадях выпускных отверстий и одинаковом гранулометрическом… Исследованиями установлено, что при выпуске руды из отверстий прямоугольного сечения форма фигуры выпуска зависит от…

Параметры эллипсоидов выпуска

Исследования показали, что по условиям выпуска шихтовые материалы могут быть разделены на две категории: а) кусковые, с преобладанием (до 90 %) фракции >5 мм; б) мелкие, с преобладанием (до 50-60 %) мелочи фрак­ции < 5 мм.

Зависимость объема эллипсоида выпуска от его высоты

Для мелких руд

В процессе опытов была выявлена зависимость объема и эксцентриситета эллипсоидов выпуска от высоты слоя руды. На рис. 8.5 приведены зависимости изменения эксцентрисите­та, малой и большой… При анализе данных установлена весьма важная за­кономерность, что с увеличением высоты эллипсоида выпуска на­блюдается…

ОГЛАВЛЕНИЕ

 

ВВЕДЕНИЕ. 3

1. ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА 8

ЖИДКОСТЕЙ И ГАЗОВ.. 8

1.1. Определение жидкости. 8

1.2. Плотность жидкости. 9

1.3. Вязкость жидкостей. 12

1.4. Поверхностное натяжение жидкости. 16

1.5. Явление смачивания. 18

1.6. Дисперсные системы.. 21

1.7. Вспенивание, физические эффекты при вспенивании. 22

1.8. Коалесценция и коагуляция диспергированных частиц. 23

1.9. Флотация дисперсной фазы.. 25

1.10. Влияние поверхностного натяжения и явления смачивания

на кристаллизацию стали. 26

2. РАВНОВЕСИЕ ЖИДКОСТИ И ГАЗА.. 29

2.1. Понятие напряженного состояния жидкости. 29

2.2. Гидростатическое давление и его свойства. 30

2.3. Дифференциальное уравнение равновесия жидкости

(уравнение Эйлера) 31

2.4. Распределение давления в покоящейся жидкости. 33

2.5. Равновесие несмешивающихся жидкостей. 35

2.6. Движение резервуара с жидкостью с постоянным ускорением (а) 36

2.7. Давление жидкости на плоскую поверхность. 39

2.8. Давление жидкости на криволинейные поверхности

(закон Архимеда) 40

3. ОСНОВЫ КИНЕМАТИКИ И ДИНАМИКИ

ЖИДКОСТИ И ГАЗОВ.. 42

3.1. Понятие кинематики. 42

3.2. Два метода описания движения сплошной среды.. 42

3.3. Линии тока, трубки тока, траектории. 43

3.4. Уравнение неразрывности. 44

3.5. Уравнение баланса импульса. 45

3.6. Уравнение Навье–Стокса. 45

3.7. Уравнение Бернулли. 46

3.8. Понятие турбулентного и ламинарного режимов движения жидкостей

и газов. 47

3.8.1. Ламинарное равномерное движение жидкости в трубах. 48

3.8.2. Турбулентные касательные напряжения. 50

4. ПОТЕРИ ЭНЕРГИИ ПРИ ДВИЖЕНИИ ЖИДКОСТИ И ГАЗОВ.. 53

4.1. Потери энергии на трение. 54

4.2. Потери энергии на местные сопротивления. 59

4.2.1. Внезапное расширение. 59

4.2.2. Диффузоры.. 62

4.2.3. Внезапное сужение. 64

4.2.4. Конфузоры.. 65

4.2.5. Потери давления на поворотах. 66

4.3. Расчет гидравлического сопротивления трубопроводов. 70

4.3.1. Простые трубопроводы.. 71

5. ИСТЕЧЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ.. 76

5.1. Истечение жидкости из отверстий. 76

5.2. Истечение жидкости через насадки. 78

5.3. Истечение жидкости при переменном уровне. 80

5.4. Формулы для гидравлического расчета открытых русел. 80

5.5. Истечение несжимаемого газа. 81

5.6. Истечение газа под высоким давлением. 84

5.7. Движение жидкости сквозь пористые среды

(ламинарная фильтрация) 85

5.8. Режимы движения двухфазных потоков в трубопроводах

(основы расчета пневмотранспорта) 87

6. Осаждение (всплывание) твердых частиц

в жидкости.. 92

6.1. Сопротивление при обтекании твердого тела. 92

6.2. Особенности осаждения (всплывания) капель жидкости

и газовых пузырей. 96

7. ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА СЫПУЧИХ МАТЕРИАЛОВ.. 100

7.1. Основные понятия и определения. 100

7.2. Физико-механические свойства шихтовых материалов. 102

8. ОСНОВНЫЕ ЗАКОНОМЕРНОСТИ ВЫПУСКА

ШИХТОВЫХ МАТЕРИАЛОВ.. 108

8.1. Постоянство расхода сыпучего материала. 108

8.2. Эллипсоид выпуска. 111

8.2.1. Зависимость эксцентриситета эллипсоида выпуска от его высоты 113

8.2.2. Влияние гранулометрического состава сыпучего материала и влажности на объем эллипсоида выпуска. 114

8.2.3. Влияние формы и размеров. 116

8.2.4. Параметры эллипсоидов выпуска. 117

8.2.5. Зависимость объема эллипсоида выпуска от его высоты

для мелких руд. 118

8.3. Эллипсоид разрыхления. 118

8.4. Воронка выпуска. 125

8.5. Скорость движения частиц без учета затухания

ее в зоне разрыхления. 126

8.6. Поверхности равных скоростей движения

частиц в потоке сыпучего материала. 132

8.7. Скорость движения частицы в потоке сыпучего материала. 135

8.8. Влияние удельного веса и размеров частиц сыпучего

материала на скорость движения их к выпускному отверстию.. 138

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 140

 

 

Учебное пособие

 

 

Сергей Александрович Загайнов

Елизавета Юрьевна Лозовая

 

МЕХАНИКА ЖИДКОСТЕЙ, ГАЗОВ И СЫПУЧИХ СРЕД

Редактор издательства Корректор Компьютерная верстка Е.Ю.Лозовой