Среднее ускорение при неравномерном движении

.

Принцип относительности Галилея (в классической механике) – никакие опыты, проводимые в инерциальных системах отсчета с механическими приборами, не позволяют установить, покоится система отсчета или движется равномерно и прямолинейно по отношению к другой инерциальной системе отсчета. Предполагается, что время не зависит от относительного движения систем отсчета.

Преобразования Галилея определяют положение произвольной материальной точки в двух инерциальных системах отсчета, одна из которых движется со скоростью v_o относительно другой (при условии, если направление скорости v₀ совпадает с направлением r_o):

r = r^' + r₀ = r' + v_ot; t = t^',

где rи r^' – радиус-векторы, определяющие положение материальной точки в неподвижной и подвижной системе отсчета в данный момент времени;

r_o – радиус вектор, определяющий положение начала координат системы К^' (подвижной) в системе К (неподвижной).

В проекциях на оси координат в произвольный момент времени t положение выбранной точки в системе К можно определить так:

x = x^' + v_0xt, x^' = x – v_0xt,

у = у^' + v_0уt, у^' = у – v_0уt,

z = z^' + v_0zt, z^' = z – v_0zt,

t = t^'. t = t^'.

Ковариантные или инвариантные уравнения – уравнения, обе части которых при переходе от одной системы координат к другой преобразуются одинаково и сохраняют свой вид во всех инерциальных системах отсчета.

Закон сложения скоростей в классической механике:

v= v^' + v₀.

Относительное расстояние между выбранными точками пространства в системах отсчета определяется соотношением – они абсолютны, т.е. инвариантны:

1) в подвижной:

;

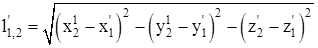2) в неподвижной:

.

Инварианты преобразований – инвариантные величины (расстояния между телами (точками), промежутки времени между событиями, относительные скорости тел, ускорения).

Вращательное движение твердого тела вокруг неподвижной оси –движение, при котором какие-либо две его точки остаются неподвижными в процессе движения. Прямая, проходящая через эти точки, – ось вращения; все остальные точки твердого тела описывают окружности в плоскостях, перпендикулярных к оси вращения, центры которых лежат на этой оси (рис. П1.3).

Основные кинематические характеристики вращательного движения (рис. П1.4):

1) угол поворота Dj – угол, отсчитанный между двумя последовательными положениями радиуса R;

2) угловая скорость w – векторная физическая величина, показывающая, как изменяется угол поворота Dj в единицу времени, численно равная первой производной от угла поворота по времени. Вектор угловой скорости направлен вдоль оси вращения в сторону, определяемую правилом правого винта:

.

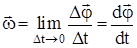3) угловое ускорение e – векторная физическая величина, характеризующая изменение угловой скорости в единицу времени, численно равная первой производной от угловой скорости по времени или второй производной от угла поворота по времени Направление вектора углового ускорения совпадает с направлением вектора угловой скорости в случае ускоренного вращения и противоположно – в случае замедленного:

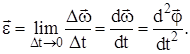
Период вращения (T) – время, в течение которого тело совершает один полный оборот.

Частота вращения (n) – число оборотов, совершаемых в единицу времени.

Круговая (циклическая) частота ω – число оборотов, совершаемых за время, равное 2π.

Связь между периодом, частотой и круговой частотой:

ω = 2π n = 2π / T; n = 1 / T.

Связь между линейными и угловыми скоростями и ускорениями

Колебательные движения (колебания) – движения или процессы, обладающие повторяемостью во времени.

Гармонические колебания (простейший вид колебаний) – движения, при которых смещение материальной точки (тела) от положения равновесия изменяется по закону синуса или косинуса (рис. П1.5):

x = x₀×sin (w₀t + j₀),

где x – смещение это удаление материальной точки от положения равновесия в данный момент времени t;

x₀ – амплитуда колебаний это максимальное удаление материальной точки от положения равновесия;

(wt + j₀) – фаза колебаний. Периодически изменяющийся аргумент функции, описывающей колебательный или волновой процесс. Определяет положение материальной точки в данный момент времени t;

j₀ – начальная фаза колебаний. Определяет положение материальной точки в начальный момент времени t = 0;

w = 2p / T = 2p n – круговая (циклическая) частота колебаний;

T – период колебаний;

n – частота колебаний.

Скорость при гармоническом колебательном движении (колебательная скорость) – физическая величина, которая показывает, как изменяется смещение в единицу времени, численно равная первой производной от смещения по времени:

.

Ускорение при гармоническом колебании – физическая величина, которая показывает, как изменяется скорость в единицу времени, численно равная первой производной от скорости или второй производной от смещения по времени:

.

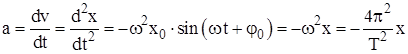Знак «минус» означает, что ускорение направлено в сторону, противоположную смещению.

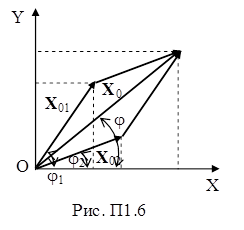
Сложение гармонических колебаний одного направления (рис. П1.6) с одинаковыми амплитудами и частотами (x₀₁ = x₀₂; w₁ = w₂ = = w), но разными начальными фазами (j₀₂ ¹ j₀₁) проводят аналитически. Уравнение результирующего колебания имеет вид

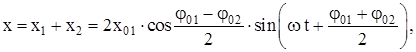
где 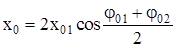– амплитуда результирующего колебания;

– фаза результирующего колебания.

Биениявозникают при сложение колебаний одного направления (рис. П1.7), с одинаковыми амплитудами (x₀₂ = x₀₁), начальными фазами j₀₁ = j₀₂ = 0 и круговыми частотами, мало отличающимися друг от друга (w₁ » w₂). Уравнения таких колебаний имеют вид

x₁ = x₀₁×sin w₁t; x₂ = x₀₁×sin w₂t.

Уравнение результирующего колебания:

,

где 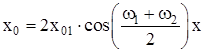– амплитуда результирующего колебания, которая зависит от Dw = w₁ – w₂ – разности частот складываемых колебаний;

– смещение результирующего колебания, изменяющееся по гармоническому закону.

Частота и период результирующего колебания:

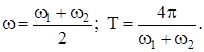
Частота и период изменения амплитуды в этом случае:

Сложение взаимно перпендикулярных колебаний приводит к тому, что траектория движения представляет собой замкнутые фигуры, называемые фигурами Лиссажу (рис. П1.8):

1) сложение колебаний с одинаковыми частотами (w₁ = w₂ = w), различными амплитудами (x₀ ¹ y₀) с начальными фазами j₁ = j₂ = 0 – результирующее колебание – гармоническое. Траектория движения – прямая линия, уравнение которой имеет вид

y = (y₀/x₀)×x.

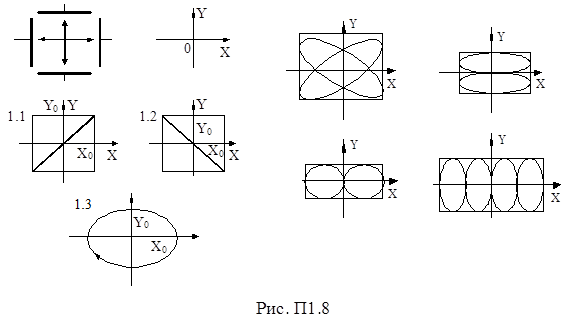
2) сложение колебаний, начальные фазы j₁ и j₂ которых отличаются на p/2 (j₁ – j₂ = p/2) – результирующее колебание – гармоническое. Траектория движения – эллипс (при равных амплитудах x₀ = y₀ – траектория результирующего движения – окружность) с полуосями, равными x₀ и y₀, уравнение которого

(y/y₀)² + (x/x₀)² = 1;

3) сложение колебаний, периоды которых относятся как целые числа – через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка возвращается в начальное положение – получаются фигуры Лиссажу более сложной формы.

Динамика изучает движение и взаимодействия тел совместно с причинами, обусловливающими тот или иной характер движения и взаимодействия.

Основная задача динамики – для данного тела по известной силе найти его ускорение и, наоборот, по известному ускорению найти результирующую силу, действующую на тело.

Массаm – физическая величина, характеризующая количество вещества, инертность, гравитационные свойства и энергию материального тела. Массу тела, определяющую его инертные свойства, называют инертной массой.

Центр масс (или центр инерции) системы – воображаемая точка С, положение которой характеризует распределение массы этой системы и определяется радиус-вектором:

,

где m_i и r_i – соответственно масса и радиус-вектор i-й материальной точки;

n – число материальных точек в системе.