рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Конденсированное состояние. Кинематика и динамика жидкостей
Реферат Курсовая Конспект
Конденсированное состояние. Кинематика и динамика жидкостей
Конденсированное состояние. Кинематика и динамика жидкостей - раздел Механика, Федеральное агенТство по образованию Жидкость – Агрегатное Состояние Вещества, Промежуточное Между Твердым И Газоо...
Жидкость – агрегатное состояние вещества, промежуточное между твердым и газообразным состояниями.
Чистые жидкости по химическому составу – однокомпонентные жидкости.
Жидкие смеси (растворы) по химическому составу – двух- или многокомпонентные жидкости.
Нормальные (обычные) жидкости – однородные макроскопические и изотропные жидкости. При отсутствии внешних воздействий обладают только одной жидкой фазой.
Квантовые жидкости – жидкости, которые могут находиться в нормальной и одной или нескольких анизотропных фазах.
Простые жидкости – жидкости, состоящие из сферически симметричных молекул, между которыми действуют силы Ван-дер-Ваальса, не имеющие какого-либо преимущественного направления и обладающие наиболее простыми свойствами.
Ближний порядок – упорядоченное расположение по отношению к любой молекуле ближайших к ней соседей.
Зависимость между временем t одного колебания молекулы относительно данного положения и временем «оседлой» жизни t0:
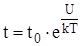
где U – «потенциальный барьер», численно равный разности энергий молекулы в двух возможных областях ее колебаний, разделяющий две возможные области колебаний молекулы;
Т – температура жидкости;
k – постоянная Больцмана.
Число молекул жидкости в некотором сферическом слое толщиной dr на расстоянии r от произвольно выбранной молекулы
,
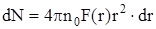где n0 = N/V – число молекул в единице объема жидкости;
F(r) – радиальная функция распределения, которая определяет вероятность нахождения некоторой молекулы жидкости в какой-либо точке ее объема.
Вязкость – свойство жидкостей оказывать сопротивление перемещению одной их части относительно другой. Определяется их молекулярным составом и строением.
Основной закон вязкого течения (закон Ньютона):
,
где dv/dz – градиент скорости в направлении z;
S – площадь слоя, по которому происходит сдвиг;
h – коэффициент динамической вязкости, который характеризует сопротивление жидкости смещению ее слоев.
Зависимость коэффициента вязкости жидкостей от температуры:
,
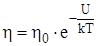где U – энергия, необходимая для перехода молекулы жидкости из одного равновесного состояния в другое.
Кинематическая вязкость – отношение динамической вязкости к плотности жидкости:
n = h/r.
Текучесть жидкостей – свойство, обратное вязкости, обусловлено той свободой движения молекул в объеме, которая еще допускается силами сцепления между ними.
Коэффициент текучести (или текучесть)
j = 1/h.
Сжимаемость – способность жидкости изменять свой объем под действием всестороннего давления.
Коэффициент сжимаемости – выражает уменьшение единичного объема (или плотности) при увеличении давления на единицу:
,
где DV, Dρ – изменение первоначального объема и первоначальной плотности жидкости при изменении давления на Dp.
Уравнение состояния жидкости (с определенной степенью точности):
.
Сфера действия молекулярных сил – область, в которой расположены взаимодействующие молекулы, в центре которой находится рассматриваемая молекула (R ~ 10-9 м).
Экспериментальный закон зависимости объема жидкости от температуры:
Vt = V0(1 + at),
где a – коэффициент объемного расширения, который определяется соотношением
.
Связь коэффициентов сжимаемости и объемного расширения жидкостей:
.
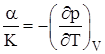Поверхностное натяжение – мера некомпенсированности межмолекулярных сил в поверхностном (межфазном) слое.
Работа dA по изменению поверхности жидкости на dS совершается за счет изменения потенциальной энергии поверхностного слоя (поверхностной энергии жидкости) dWps:
dA = –dWps = –s×dS,
где «минус» показывает, что увеличение поверхности жидкости сопровождается совершением работы;
s – коэффициент поверхностного натяжения, который характеризует свойства поверхности жидкости и показывает, какую работу необходимо совершить, чтобы увеличить поверхность жидкости на единицу.
Работа по изменению поверхности жидкости, совершаемая внешними силами:
dA = –F×dx = –s×dS = –sℓ×dx,
где ℓ – длина контура, охватывающего поверхность жидкости;
dx – смещение границы поверхностного слоя;
F – сила поверхностного натяжения;
s – коэффициент поверхностного натяжения, который численно равен силе поверхностного натяжения, стремящейся изменить длину контура, охватывающего поверхность жидкости, на единицу.
Зависимость коэффициента поверхностного натяжения от температуры:
,
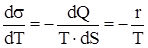где r = dQ/dS – количество тепла, затраченное на изменение поверхности пленки на единицу.
Полное молекулярное давление в поверхностном слое жидкости
p = p0 ± Dp,
где p0 – молекулярное давление жидкости с плоской поверхностью;
Dp – дополнительное давление, возникающее за счет кривизны поверхности жидкости;
знак «+» – соответствует выпуклой поверхности;
знак «–» – соответствует вогнутой поверхности.
Формула Лапласа для дополнительного давления (для капли, которая полностью заполнена жидкостью, или для пузырька внутри жидкости) в случае:
1) произвольной поверхности:
,
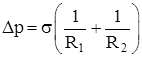где R1 и R2 – радиусы кривизны поверхностного слоя жидкости;
2) сферической поверхности:
,
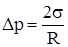где R – радиус сферы;
3) цилиндрической поверхности:
,
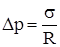где R – радиус цилиндрической поверхности.
Формула Лапласа для дополнительного давления (для пузырька, который не заполнен жидкостью, например мыльного) в случае:
1) сферической поверхности:
;
2) цилиндрической поверхности:
.
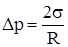Условие равновесия капли на поверхности другой жидкости:
s12 + s23 = s13,
где s12 – коэффициент поверхностного натяжения между жидкостью капли и жидкостью, на которой она находится;
s13 – коэффициент поверхностного натяжения между жидкостью, на которой находится капля, и воздухом;
s23 – коэффициент поверхностного натяжения между жидкостью капли и воздухом.
Условие равновесия капли на поверхности твердого тела:
s12 + s23×cosq = s13,
где s12 – коэффициент поверхностного натяжения между жидкостью капли и твердым телом;
s13 – коэффициент поверхностного натяжения между твердым телом и воздухом;
s23 – коэффициент поверхностного натяжения между жидкостью капли и воздухом;
q – краевой угол (угол между касательными к поверхности жидкости и твердого тела).
Условие смачивания (краевой угол острый):
s12 + s23×cosq £ s13.
Условие абсолютного смачивания:
s12 + s23×cosq < s13.
Условие несмачивания (краевой угол тупой):
s12 ³ s23×cosq + s13.
Условие абсолютного несмачивания:
s12 > s23×cosq + s13.
Капиллярные явления (капиллярность) – изменение высоты уровня жидкости в узких трубах (капиллярах) или зазорах между двумя стенками.
Условие капиллярности:
Dp = p,
где 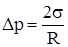– дополнительное давление, возникающее за счет кривизны поверхности жидкости при капиллярности;
p = rgh – давление;
– радиус мениска;
r – радиус капилляра;
q – краевой угол.
Высота подъема (опускания) жидкости в капиллярах
.
Высота подъема (опускания) жидкости в узком зазоре между погруженными в жидкость параллельными пластинами
,
где d – расстояние между пластинами.
Давление внутри жидкости во всех точках, расположенных на одном уровне (при механическом равновесии, если жидкость находится в поле тяготения):
p = const.
Давление в жидкости на двух разных уровнях (при механическом равновесии; жидкость находится в поле тяготения) отличается на величину, равную весу вертикального столба жидкости, заключенного между этими уровнями, с площадью сечения, равного единице:
p2 = p1 + rgh,
где p1, p2 – давления жидкости на соответствующих уровнях;
h – высота между слоями.
Закон Архимеда: «На тело, погруженное в жидкость (или газ), находящееся в механическом равновесии, действует выталкивающая сила, равная весу вытесненной телом жидкости (газа), направленная по вертикали вверх и приложенная к центру масс вытесненного объема»:
.
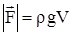Поток жидкости – совокупность частиц движущейся жидкости.
Линия тока жидкости – линия, касательная к которой совпадает с направлением скорости частицы жидкости в рассматриваемый момент времени и в данной точке пространства. Линии тока жидкости служат для графического отображения потока жидкости.
Трубка тока – часть жидкости, ограниченная линиями тока.
Установившееся (стационарное) течение жидкости – движение жидкости, при котором форма и расположение линий тока, а также значения скоростей частиц жидкости в каждой их точке не изменяются со временем.
Неустановившееся (нестационарное) течение жидкости – движение жидкости, при котором не выполняются условия стационарного движения.
Математическая форма записи теоремы (уравнения) о неразрывности (непрерывности струи) для несжимаемой жидкости:
Sv = const,
где S – площадь сечения трубки тока;
v – скорость жидкости.
Уравнение Бернулли для стационарно текущей идеальной жидкости (для жидкостей с малой вязкостью):
,
где r – плотность жидкости;
v – скорость течения жидкости;
h – высота, на которой находится некоторое сечение трубки тока;
p – давление жидкости на уровне этих сечений.
Закон изменение давления жидкости для двух сечений (с изменением высоты h сечений) при v1 = v2:
.
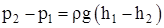Закон изменение давления жидкости для горизонтального потока (h1 = h2):
,
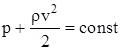где p – давление, не зависящее от скорости (статическое давление жидкости);
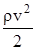– давление, зависящее от скорости (динамическое давление), которое показывает, на какую величину изменяется статическое давление при остановке движущегося потока жидкости.
Полное давление потока жидкости – сумма статического и динамического давлений.
Монометрические трубки (трубки Пито) – приборы, с помощью которых измеряют статическое и полное давление жидкости.
Скорость течения вязкой жидкости в трубе
,
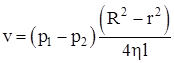где p1, p2 – давления двух сечений трубы;
R – радиус трубы;
r – расстояние от центра трубы до рассматриваемой трубки тока;
h – коэффициент вязкости жидкости;
l – расстояние между сечениями трубы.
Формула Пуазейля для определения объема жидкости, прошедшего через сечения трубы:
.
Ламинарное (слоистое) течение жидкости – когда жидкость как бы разделяется на слои, скользящие относительно друг друга, не перемешиваясь. Ламинарное течение жидкости стационарно.
Турбулентное течение жидкости – когда происходит энергичное перемешивание жидкости. В этом случае скорость частиц в каждом месте изменяется хаотично, течение – нестационарное.
Число Рейнольдса определяет характер течения жидкости:
, 
,
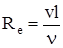где r – плотность жидкости;
v – средняя по сечению скорость движения жидкости;
l – характерный для поперечного сечения размер;
h – динамическая вязкость;
n – кинематическая вязкость.
– Конец работы –
Эта тема принадлежит разделу:
Федеральное агенТство по образованию
Государственное образовательное учреждение... высшего профессионального образования... Курский государственный технический университет...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Конденсированное состояние. Кинематика и динамика жидкостей
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?
Подпишитесь на Нашу рассылку
Реклама
Информация в виде рефератов, конспектов, лекций, курсовых и дипломных работ имеют своего автора, которому принадлежат права. Поэтому, прежде чем использовать какую либо информацию с этого сайта, убедитесь, что этим Вы не нарушаете чье либо право.
© copyright 1999 - 2024 allRefs.net. Все права защищены. Страница сгенерирована за: 0.028 сек.
Новости и инфо для студентов