рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Основные положения и законы термодинамики
Реферат Курсовая Конспект
Основные положения и законы термодинамики
Основные положения и законы термодинамики - раздел Механика, Федеральное агенТство по образованию 1. Первое Начало Термодинамики Гласит: «Изменение Внутренней Энергии Системы ...
1. Первое начало термодинамики гласит: «Изменение внутренней энергии системы при переходе из одного состояния в другое равно сумме механических эквивалентов всех внешних воздействий». Математически это можно записать так: 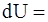
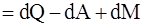 , где dU – изменение внутренней энергии системы; dQ – элементарное количество тепла, подводимого к системе; dA – элементарная работа, совершаемая системой; dM – другие виды элементарных энергий. Можно ли утверждать, что оно является:
, где dU – изменение внутренней энергии системы; dQ – элементарное количество тепла, подводимого к системе; dA – элементарная работа, совершаемая системой; dM – другие виды элементарных энергий. Можно ли утверждать, что оно является:
а) законом сохранения и превращения энергии, которым сопровождаются термодинамические процессы;
б) утверждением, согласно которому термодинамическая система может совершать работу только за счёт своей внутренней энергии;
в) утверждением, согласно которому термодинамическая система может совершать работу не только за счёт каких-либо внешних источников энергии;
г) утверждением о невозможности существования вечных двигателей первого рода, который совершал бы работу, не потребляя энергию из какого-либо внешнего источника.
2. Соотношение, которое полностью отображает первое начало термодинамики:
а) 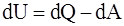 ;
;
б)  ;
;
в) 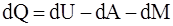 ;
;
г) 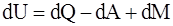 .
.
3. Первое начало термодинамики утверждает, что:
а) каждое состояние термодинамической системы характеризуется определённым значением внутренней энергии U, независимо от того, каким путём система приведена в данное состояние;
б) внутренняя энергия термодинамической системы U является функцией состояния системы;
в) каждое состояние термодинамической системы характеризуется определённым значением внутренней энергии U, в зависимости от того, каким путём система приведена в данное состояние.
4. Первое начало термодинамики утверждает, что:
а) работа, совершаемая термодинамической системой, зависит от процесса, приведшего к изменению состояния системы;
б) количество тепла, сообщенное термодинамической системе, зависит от процесса, приведшего к изменению состояния системы;
в) работа, совершаемая термодинамической системой, является функцией состояния системы;
г) количество тепла, сообщенное термодинамической системе, является функцией состояния системы.
5. Формула, представляющая собой математическую запись первого начала термодинамики для произвольной массы газа:
а) 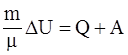 ;
;
б) 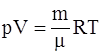 ;
;
в) 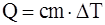 ;
;
г) 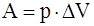 .
.
6. Изотермический процесс – процесс, протекающий при постоянной температуре (T = const). При изотермическом процессе:
а) внутренняя энергия системы изменяется;
б) внутренняя энергия системы остаётся величиной постоянной;
в) все подводимое к системе тепло идет на совершение этой системой работы;
г) часть подводимого к системе тепла идет на совершение этой системой работы.
7. Работа, совершаемая произвольной массой m идеального газа при изотермическом процессе, определяется соотношением:
а)  ;
;
б) 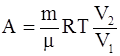 ;
;
в) 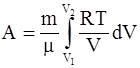 ;
;
г) 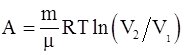 .
.
8. Изобарический процесс – процесс, протекающий при постоянном давлении (p = const). При этом подводимое к системе тепло идёт:
а) как на изменение ее внутренней энергии, так и на совершение этой системой работы;
б) только на изменение ее внутренней энергии;
в) только на совершение этой системой работы.
9. Работа, совершаемая произвольной массой m идеального газа при изобарическом процессе, определяется соотношением:
а) 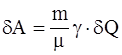 ;
;
б)  ;
;
в)  ;
;
г)  .
.
10. Изменение внутренней энергии произвольной массы m идеального газа при изобарическом процессе определяется соотношением:
а)  ;
;
б)  ;
;
в) 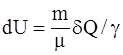 .
.
11. Если температура идеального газа увеличилась в 4 раза, то его внутренняя энергия увеличилась в:
а) 4 раза;
б) 2 раза;
в) 1,5 раза;
г) 2,5 раза;
д) не изменилась.
12. Изохорический процесс – это процесс, протекающий при постоянном объеме (V = const). При этом все подводимое к системе тепло идет на изменение ее внутренней энергии. Какие из приведенных соотношений справедливы в данном случае?
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
13. Адиабатический процесс – это процесс, протекающий без теплообмена или почти без теплообмена с окружающей средой. При этом работа:
а) может совершаться системой только за счет убыли её внутренней энергии;
б) может совершаться системой только за счет возрастания её внутренней энергии;
в) может совершаться системой только за счет энергии из других внешних источников.
14. Какие из приведенных соотношений справедливы для адиабатического процесса (являются уравнениями Пуассона)?
а) 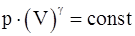 ;
;
б)  ;
;
в)  ;
;
г) 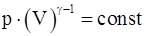 .
.
15. Работа, совершаемая произвольной массой m идеального газа при адиабатическом расширении, определяется по формуле:
а)  ;
;
б) 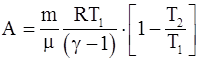 ;
;
в)  .
.
16. Если ΔU – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для адиабатного расширения газа справедливы следующие соотношения:
а) Q > 0; A > 0; ΔU = 0;
б) Q = 0; A > 0; ΔU < 0;
в) Q < 0; A < 0; ΔU = 0;
г) Q = 0; А < 0; ΔU > 0.
17. Если над термодинамической системой внешними силами совершается работа A и той же системе передаётся некоторое количество теплоты Q, то этом случае изменение внутренней энергии DU системы будет равно:
а) DU = A;
б) DU = Q;
в) DU = A + Q;
г) DU = A – Q.
18. Какие из приведенных соотношений справедливы для политропического процесса?
а)  ;
;
б)  ;
;
в) 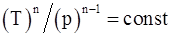 ;
;
г)  .
.
19. Работа, совершаемая произвольной массой m идеального газа при политропическом процессе:
а) 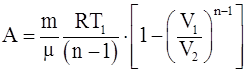 ;
;
б)  ;
;
в) 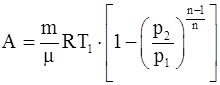 .
.
20. Если переданное идеальному газу количество теплоты в любой момент времени равно работе, совершённой газом, то можно утверждать, что в данном газе совершается:
а) адиабатический процесс;
б) изотермический процесс;
в) изобарический процесс;
г) изохорический процесс.
21. Если переданное идеальному газу количество теплоты в любой момент времени равно изменению внутренней энергии газа, то можно утверждать, что в данном газе совершается:
а) адиабатический процесс;
б) изотермический процесс;
в) изобарический процесс;
г) изохорический процесс.
22. Если в любой момент времени совершенная идеальным газом работа равна изменению внутренней энергии термодинамической системе, то можно утверждать, что в данном газе совершается:
а) адиабатический процесс;
б) изотермический процесс;
в) изобарический процесс;
г) изохорический процесс.
23. Внутренняя энергия тела может изменяться:
а) только при передаче телу некоторого количества теплоты;
б) только при совершении внешними силами над телом механической работы;
в) при изменении кинетической и потенциальной энергии тела как целого;
г) при передаче телу теплоты и при совершении над ним работы.
24. При изобарическом процессе работа газа всегда:
а) равна нулю;
б) положительна;
в) отрицательна;
г) зависит от величины давления и от изменения объема.
25. Работа, совершаемая идеальным газом при круговом процессе (цикле):
а) эквивалентна разности количеств тепла, подводимого к системе при расширении Q1 и отводимого от нее при сжатии Q2;
б) эквивалентна разности количеств тепла, отводимого от системы при сжатии Q2 и подводимого к системе при расширении Q1;
в) равна разности работ при расширении А1 и при сжатии А2 газа;
г) равна разности работ при при сжатии А2 и расширении А1 газа.
26. Коэффициент полезного действия кругового процесса (цикла) – это:
а) физическая величина, равная отношению работы цикла к работе, которую можно было бы совершить при превращении в нее всего количества тепла, подведенного к системе;
б) физическая величина, равная отношению разности количества тепла, подведенного к системе, и количества тепла, отданного системой, к количеству тепла, отданного системой;
в) физическая величина, равная отношению разности количества тепла, подведенного к системе, и количества тепла, отданного системой, к работе, которую можно было бы совершить при превращении в нее всего количества тепла, подведенного к системе.
27. Цикл Карно – это:
а) цикл, состоящий из последовательно чередующихся двух изотермических и двух адиабатических процессов, осуществляемых с рабочим телом (например, паром);
б) цикл, состоящий из последовательно чередующихся двух адиабатических и двух изотермических процессов, осуществляемых с рабочим телом (например, паром);
в) обратимый круговой процесс, в котором совершается превращение теплоты в работу (или работы в теплоту);
г) необратимый круговой процесс, в котором совершается превращение теплоты в работу (или работы в теплоту).
28. Тепловая машина работает по циклу Карно. Если температуру нагревателя увеличить, то КПД цикла:
а) не изменится;
б) увеличится;
в) уменьшится.
29. На рисунке 1 изображен цикл Карно в координатах (T,S), где S – энтропия. Изотермическое расширение происходит на этапе:
| а) 3 – 4; б) 1 – 2; в) 4 – 1; г) 2 – 3. | 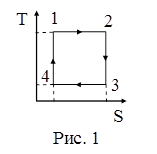
|
30. Математически первое начало термодинамики для изотермического процесса можно отобразить следующими соотношениями:
а) T = const; PV = const; U = const;
б) T = const; PV/R = const; U = 0;
в) PV = const; Q = DU; Aг = 0;
г) T = const; Q = Aг; DU = 0.
31. Работа, совершаемая произвольной массой m идеального газа цикл Карно, определяется соотношением:
а)  ;
;
б) 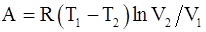 ;
;
в) 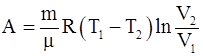 .
.
32. На рисунке 1 в координатах p – V представлен цикл Карно. На участке АВ рабочее тело приводится в соприкосновение с нагревателем, находящимся при температуре T1, и:
| а) расширяясь, совершает работу; б) только расширяется; в) только совершает работу; г) изотермически получает от нагревателя некоторое количество тепла. | 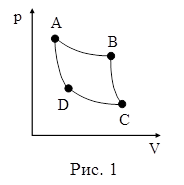
|
33. На рисунке 1 в координатах p – V представлен цикл Карно. На участке ВС рабочее тело:
| а) расширяясь адиабатически, совершает работу; б) только расширяется; в) только совершает работу; г) адиабатически охлаждается до температуры Т2. | 
|
34. На рисунке 1 в координатах p – V представлен цикл Карно. На участке СD рабочее тело:
| а) сжимаясь адиабатически, совершает работу; б) сжимаясь изотермически, совершает работу; в) сжимаясь изотермически, совершает работу; г) сжимаясь изотермически, отдаёт некоторое количество тепла. | 
|
35. На рисунке 1 в координатах p – V представлен цикл Карно. На участке АD рабочее тело:
| а) сжимаясь адиабатически, отдаёт холодильнику некоторое количество тепла; б) сжимаясь изотермически, совершает работу; в) сжимаясь изотермически, не совершает работу; г) сжимаясь изотермически, отдаёт холодильнику некоторое количество тепла. | 
|
36. На рисунке 1 в координатах p – V представлен цикл Карно. В точке В температура рабочего тела равна температуре точки:
| а) А; б) С; в) D. | 
|
37. На рисунке 1 в координатах p – V представлен цикл Карно. В точке C температура рабочего тела равна температуре точки:
| а) А; б) С; в) D. | 
|
38. На рисунке 1 в координатах p – V представлен цикл Карно. В точке D температура рабочего тела равна температуре точки:
| а) А; б) С; в) D. | 
|
39. На рисунке 1 в координатах p – V представлен цикл Карно. Работа данного цикла численно равна площади фигуры:
| а) АBMNA; б) DCLKD; в) ABСD; г) ADKNA. | 
|
40. Коэффициент полезного действия цикла Карно h:
а) не зависит от природы вещества;
б) зависит от природы вещества;
в) зависит лишь от температур, при которых теплота сообщается системе и отбирается от нее;
г) не зависит от температур, при которых совершаются последовательные изотермические и адиабатические процессы.
41. На рисунке 1 в координатах p – V представлен цикл Карно. Коэффициент полезного действия цикла Карно h определяется соотношением:
а)  ;
б) ;
б) 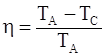 ; ;
| в) 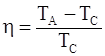 ;
г) ;
г) 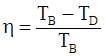 . .
| 
|
42. На рисунке 1 в координатах p – V представлен цикл Карно. Коэффициент полезного действия цикла Карно h численно равен отношению:
| а) площади фигуры ABCDA к площади фигуры ABMNA; б) площади фигуры ABCDA к площади фигуры CLKDC; в) разности площадей фигур ABMNA и CLKDC к площади фигуры ABMNA; г) разности площадей фигур ABMNA и CLKDC к площади фигуры CLKDC; д) среди приведенных ответов правильного ответа нет. | 
|
43. На рисунке 1 в координатах p – V представлен цикл Карно. Коэффициент полезного действия холодильной машины (холодильника) 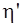 определяется соотношением:
определяется соотношением:
а)  ;
б) ;
б) 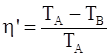 ; ;
| в) 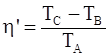 ;
г) ;
г)  . .
| 
|
44. На рисунках 1–3 в координатах p – V представлены циклы Карно, Отто и Дизеля. Циклу Отто соответствует рисунок:
| а) 1; б) 2; в) 3. | 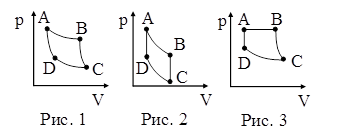
|
45. На рисунках 1–3 в координатах p – V представлены циклы Карно, Отто и Дизеля. Циклу Дизеля соответствует рисунок:
| а) 3; б) 2; в) 1. | 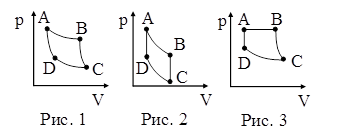
|
46. На рисунках 1–3 в координатах p – V представлены циклы Карно, Отто и Дизеля. Циклу Карно соответствует рисунок:
| а) 3; б) 2; в) 1. | 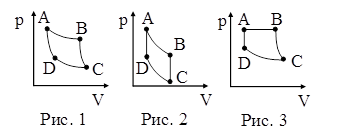
|
47. За один цикл тепловая машина, коэффициент полезного действия которой h = 50 %, отдаёт холодильнику 500 Дж теплоты. В этом случае работа, совершаемая тепловой машиной, равна:
а) 1000 Дж
б) 750 Дж;
в) 500 Дж;
г) 250 Дж.
48. За один цикл тепловая машина, коэффициент полезного действия которой h = 50 %, получает от нагревателя 500 Дж теплоты. В этом случае работа, совершаемая тепловой машиной, равна:
а) 1000 Дж
б) 750 Дж;
в) 500 Дж;
г) 250 Дж.
49. За один цикл тепловая машина, коэффициент полезного действия которой h = 50 %, совершает работу в 500 Дж. В этом случае тепловая машина отдаёт холодильнику:
а) 1000 Дж теплоты;
б) 750 Дж теплоты;
в) 500 Дж теплоты;
г) 250 Дж теплоты.
50. Газ совершает работу против внешних сил 500 Дж, получая из вне 500 Дж теплоты. В этом случае изменение внутренней энергии газа равно:
а) 0 Дж;
б) 300 Дж;
в) 200 Дж;
г) 100 Дж.
51. Если тепловая машина с КПД 50% за один цикл отдает холодильнику 500 Дж теплоты, то работа, совершаемая машиной за один цикл, равна:
а) 250 Дж;
б) 500 Дж;
в) 750 Дж;
г) 800 Дж.
52. Над термодинамической системой внешние силы совершают работу, равную A, и этой же системе передаётся количество тепла, равное Q. Изменение внутренней энергии термодинамической системы ∆U в этом случае равно:
а) 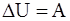 ;
;
б)  ;
;
в) 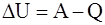 ;
;
г)  .
.
53. Абсолютная температура нагревателя в идеальной тепловой машине вдвое больше температуры холодильника, КПД такой машины равен:
а) 600 %;
б) 50 %;
в) 40 %;
г) 30 %.
54. Если температура нагревателя идеальной тепловой машины 227ºС, а температура холодильника 27ºС, то газ в машине совершает полезную работу, равную:
а) 0,4 Q;
б) 0,5 Q;
в) 0,6 Q;
г) 0,7 Q.
55. КПД идеальной тепловой машины, которая совершает полезную работу 200 Дж, получая для этого 800 Дж теплоты, равен:
а) 40 %;
б) 10 %;
в) 20 %;
г) 25 %.
56. Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке 1. Отношение работы при нагревании газа к работе при охлаждении равно:
| а) 3; б) 5; в) 1,5; г) 2,5. | 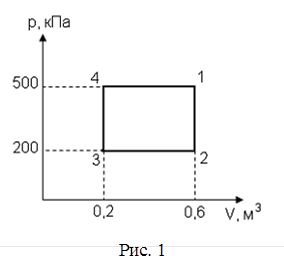
|
57. В идеальной тепловой машине абсолютная температура нагревателя вдвое больше температуры холодильника. Если, не меняя температуру нагревателя, температуру холодильника уменьшить вдвое, то КПД этой машины:
а) возрастет на 20 %;
б) возрастет на 25 %;
в) возрастет на 30 %;
г) возрастет на 35 %.
58. Энтропия – это:
а) физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно только полученному количеству теплоты, деленному на температуру, при которой произошел этот процесс;
б) физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно только отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс;
в) физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно любому количеству теплоты, деленному на температуру, при которой произошел этот процесс;
г) физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно полученному или отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс.
59. В термодинамике энтропия – это:
а) мера обратимого и необратимого рассеяния энергии;
б) мера обратимого рассеяния энергии;
в) мера необратимого рассеяния энергии;
г) функция состояния системы, которая позволяет строго математически сформулировать второе начало термодинамики.
60. Второе начало термодинамики:
а) «В изолированной системе возможны только такие процессы, при которых энтропия системы возрастает»;
б) «В изолированной системе возможны только такие процессы, при которых энтропия системы убывает»;
в) «В изолированной системе возможны только такие процессы, при которых энтропия системы остаётся величиной постоянной»;
г) «Невозможен процесс, единственным результатом которого является превращение в работу теплоты, полученной от нагревателя».
61. Математически второе начало термодинамики отображается соотношением:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
62. Связь энтропии системы с вероятностью выражается соотношением:
а) 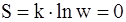 ;
;
б) 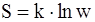 ;
;
в)  ;
;
г) 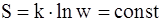 .
.
63. В общем случае изменение энтропии системы при переходе из одного состояния в другое определяется формулой:
а) 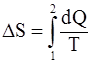 ;
;
б) 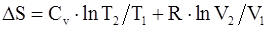 ;
;
в) 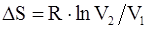 ;
;
г) 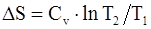 .
.
64. Изменение энтропии системы при изотермическом процессе:
а) 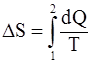 ;
;
б) 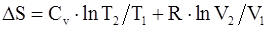 ;
;
в) 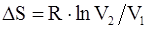 ;
;
г) 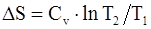 .
.
65. Изменение энтропии системы при изобарическом процессе:
а) 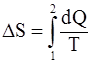 ;
;
б) 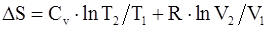 ;
;
в)  ;
;
г) 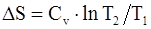 .
.
66. Изменение энтропии системы при изохорическом процессе:
а) 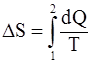 ;
;
б) 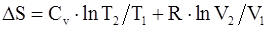 ;
;
в)  ;
;
г) 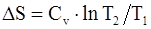 .
.
67. Изменение энтропии системы при адиабатическом процессе:
а) 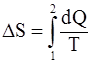 ;
;
б) 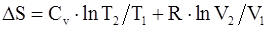 ;
;
в)  ;
;
г) 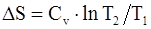 .
.
68. Изменение энтропии системы, совершающей цикл Карно:
а)  ;
;
б) 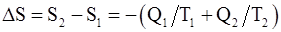 ;
;
в) 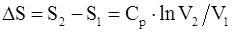 ;
;
г) 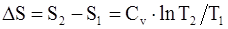 .
.
69. В случае совершения системой обратимого цикла Карно энтропия замкнутой системы:
а) изменяется;
б) не изменяется;
в) остаётся величиной постоянной;
г) уменьшается.
70. В случае совершения системой необратимого цикла Карно энтропия замкнутой системы:
а) возрастает;
б) не изменяется;
в) остаётся величиной постоянной;
г) уменьшается.
71. Для произвольных процессов, происходящих в замкнутой системе, энтропия системы:
а)  ;
;
б)  ;
;
в) 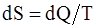 ;
;
г) 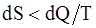 .
.
72. Для произвольных процессов, происходящих в замкнутой системе, энтропия:
а) может убывать;
б) не может убывать;
в) не может возрастать;
г) может возрастать.
73. Третье начало термодинамики (теорема Нернста) формулируется так:
а) «Изменение энтропии системы (DS) при любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при любых температурах, стремится к нулю»;
б) «Изменение энтропии системы (DS) при любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при температурах, приближающихся к абсолютному нулю, стремится к нулю»;
в) «При помощи последовательности термодинамических процессов нельзя достичь температуры, равной абсолютному нулю»;
г) «При помощи последовательности термодинамических процессов можно достичь температуры, равной абсолютному нулю».
74. Термодинамика неравновесных процессов – это:
а) общая теория макроскопического описания неравновесных процессов, позволяющая количественное изучение этих процессов для состояний, не сильно отличающихся от равновесного состояния;
б) общая теория макроскопического описания неравновесных процессов, позволяющая количественное изучение этих процессов для любых состояний;
в) общая теория макроскопического описания равновесных процессов;
г) общая теория макроскопического описания неравновесных процессов.
75. На рисунке 1 представлен цикл тепловой машины в координатах Т, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами:
| а) нагреватели – Т3, Т5, холодильники – Т1, Т2, Т4; б) нагреватели – Т3, Т4, Т5, холодильники – T1 Т2; в) нагреватели – Т4, Т5, холодильники – T1, Т2, Т3; г) нагреватели – Т2 Т4, Т5, холодильники – T1, Т3; д) среди приведенных ответов правильного ответа нет. | 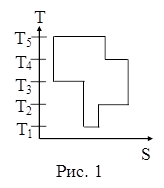
|
76. На рисунке 1 изображен цикл Карно в координатах (T,S), где S – энтропия. Изотермическое расширение происходит на этапе:
| а) 3-4; б) 1-2; в) 4-1; г) 2-3. | 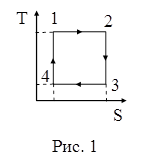
|
– Конец работы –
Эта тема принадлежит разделу:
Федеральное агенТство по образованию
Государственное образовательное учреждение... высшего профессионального образования... Курский государственный технический университет...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Основные положения и законы термодинамики
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов