Величина, равная половине произведения массы тела на квадрат его скорости.

[E_k]=Дж.

Кинетическая энергия - величина относительная, зависящая от выбора СО, т.к. скорость тела зависит от выбора СО.

Т.о.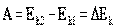

- эта формула выражает теорему о кинетической энергии: изменение кинетической энергии тела (материальной точки)за некоторый промежуток времени равно работе, совершенной силой, действующей на тело, за этот же промежуток времени

Эта теорема справедлива для любого движения и для сил любой природы. Если тело разгоняется из состояния покоя, то E_k1=0. Тогда A = E_k2. Следовательно, кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости.

Вывод: Работа силы равна изменению кинетической энергии тела, т.е. A = DE_k.Причем, A>0, если E_k увеличивается, и А<0, если E_k<0.

A = DE_k

Потенциальная энергия 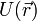— скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет его нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы^[1]. Термин «потенциальная энергия» был введен в XIX веке шотландским инженером и физиком Уильямом Ренкином.

Единицей измерения энергии в СИ является Джоуль.

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.

Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

E_p = mgh,

где E_p — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем.

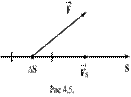
Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы , действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии . Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

Для установления этой связи вычислим элементарную работу , совершаемую силами поля при малом перемещении 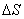тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой . Эта работа равна

где 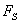- проекция силы на направление .

Поскольку в данном случае работа совершается за счет запаса потенциальной энергии , она равна убыли потенциальной энергии 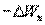на отрезке оси :

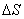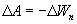
Из двух последних выражений получаем

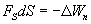
Откуда

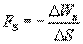
Последнее выражение дает среднее значение 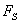на отрезке 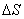. Чтобы

получить значение 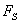в точке нужно произвести предельный переход:

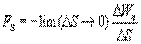
Так как может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от по :

Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

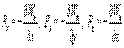
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

в математике вектор ,

где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом 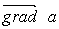. Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком

Полная механическая энергия системы – сумма ее кинетической и потенциальной энергии.

W=W_k+W_п=const (3.25)

Формула (3.25) выражает закон сохранения энергии в замкнутой системе, в которой действуют только консервативные силы: полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию и обратно.

Системы, в которых полная механическая энергия сохраняется, называют консервативными.

Для полной механической энергии закон сохранения энергии имеет следующее выражение: полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения и упругости, остается неизменной.

 

Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, перпендикулярной плоскостям этих окружностей. Сама эта прямая есть ось вращения (рис. а).

Примером такого движения может послужить: вращение колес, валов двигателей и т.д.

Угловая скорость. Каждая точка вращающегося тела движется по окружности и различные точки проходят за время Δt разные пути. Так дуга АА₁ больше дуги ВВ₁, поэтому модуль скорости точки А больше, чем точке В (рис. б). Но радиусы окружностей поворачиваются за время Δt на один и тот же угол φ. Этот угол отсчитывается между лучами, выходящими из одной точки оси и перпендикулярными ей:

· Первый луч - ОХ - неподвижен в пространстве

· Второй луч - ОА - тесно связан с телом.

Пусть тело вращается равномерно, т.е. за одинаковые промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела определяется углом поворота любого луча, связанного с телом, за данный интервал времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол π/2, а другое - на угол π/4, то мы говорим, что первое тело вращается быстрее второго.

Угловой скоростью при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени, за который этот поворот совершен.

Угловая скорость обозначается буквой ω («омега»), по определению она равна:
ω=φ/Δt.
Угловая скорость выражается в радианах в секунду (рад/с). Напомним что 1 радиан = 57°.

Угловою скорость можно выразить через частоту вращения, т.е число полных оборотов за 1 с. Если тело делает ν («ню») оборотов за 1 с, то время одного оборота равно 1/ν. Это называется периодом вращения и обозначают буквой Т.

Полному обороту тела соответствует угол φ=2π. Поэтому получим формулу:
ω=2π/Т или
ω=2πν.

Связь между линейной и угловой скоростью. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости.

При вращении твердого тела разные его точки имеют разные линейные скорости, но угловая скорость для всех точек одинакова.

Между линейной скоростью какой-либо точки вращающегося тела и угловой скорость существует связь.Точка, лежащая на окружности радиуса R, за один оборот пройдет путь 2πR. А так как, время одного оборота тела есть период Т, то модуль линейной скорости можно найти так:
v=2πR/T=2πRν или
v=ωR.

Отсюда видно, что , чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость.

Модуль ускорения точки, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:
a=v²/R, но
v=ωR. Следовательно,
a=ω²R.

Чем дальше расположена точка твердого тела от оси вращения, тем больше по модулю ускорение он имеет.