ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ. СДВИГ И КРУЧЕНИЕ

Методические указания. Проработать материал о плоском напряженном состоянии, усвоить определение напряжений по наклонной площадке:

 

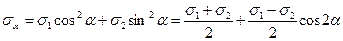
(7)

 

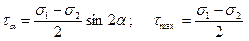
где σ₁ и σ₂ — главные напряжения.

Изучить определение величин напряжений по наклонной площадке (α), если даны нормальное и касательное напряжения по произвольным взаимно перпендикулярным площадкам σ_х, σ_у и τ_ху:

 

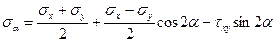
(8)

 

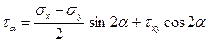
При отыскании главных напряжений τ_α=0:

 

 

 

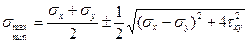
(9)

 

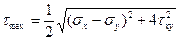
Повторить применение круга Мора для определения σ_α, τ_α по главным напряжениям и для решения обратной задачи. Знать для кручения формулы τ_r=M_кр/W_p; φ=M_крl/GI_p.

 

Задача № 6. Найти число заклёпок в прикреплении стержня, состоящего из двух уголков к фасонке толщиною δ=14 мм, если диаметр заклёпки d=20 мм, Р=38 т, допускаемые напряжения [σ] =1600 кГ/см², [τ]=1000 кГ/см², [σ_см]=2800 кГ/см² (рисунок 6).

 

Рисунок 6

 

Решение. Площадь сечения одного уголка

 

 

Считая, что толщина уголка 0,8 см, добавляем к F_н площадь ослабления ∆F=0,8d=0,8·2=1,6 см². Необходимая площадь сечения стержня 13,5 см². Берем уголок 90x90x8. Число заклёпок по двойному срезу будет равно: n=3,03, по смятию (по толщине фасонки) n=4,85. Итак, следует взять 5 заклёпок.

 

Задача № 7. Рассмотреть напряженное состояние при чистом сдвиге (рисунок 7). Найти τ_max и направление площадки, по которой оно действует. Найти нормальное и касательное напряжения по площадке, наклоненной к σ₁ под углом α=30°. Определить относительное удлинение в направлении главного напряжения σ₁ если Е=2·10⁶ кГ/см².

 

Рисунок 7

 

Дано: σ₁=1000 кГ/см²; μ=0,25.

Ответ:.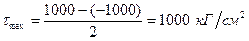
Это напряжение действует по площадкам, наклоненным под углом α₁=45° к главным направлениям (при этом σ=0). Нормальное и касательное напряжения по площадке с углом α:

 

 

 

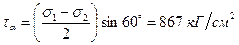
Задача № 8. Определить величины и направления главных напряжений, если σ_x=400 кГ/см²; σ_y=200 кГ/см²; τ_xy=100 кГ/см² (рисунок 8, а). Применить круг Мора.

Решение. В координатах σ÷τ строим круг Мора (рисунок 8, б). Откладываем ОК=σ_х; ОК₁=σ_y; KD=τ_xy; K₁D₁=-τ_xy. Соединяя точки D, D₁, получаем центр круга С, причем ОС=300 кГ/см². Линия CD составляет угол 2α, линия BD—угол α с осью абсцисс. Очевидно, tg2α=1, 2α=45; α=22,5^о. От направления σ_х (рисунок 8, а) откладываем по часовой стрелке угол α для σ_max. По кругу Мора σ_max=ОС + СА=ОС + CD, т. е. 300 + 100√2=441 кГ/см², σ_min=ОВ, т. е. 159 кГ/см².

 

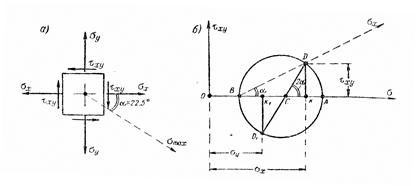
Рисунок 8

Задача № 9. Найти нормальное и касательное напряжения по заданным главным напряжениям σ₁ и σ₂=σ₁/2, по кругу Мора, если угол наклона площадки к направлению σ₁ - α=30° (рисунок 9, a).

 

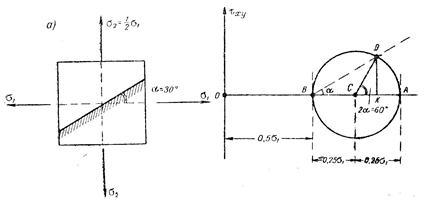
Рисунок 9

Решение. Откладываем (рисунок 9, б) ОА=σ₁; ОВ=σ₂=0,5σ₁. Радиус круга – 0,25σ₁.

Тогда:

 

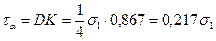
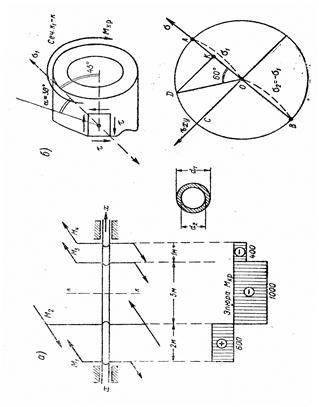
Рисунок 10

Задача № 10. Построить эпюру крутящих моментов и определить наружный диаметр полого вала d₁, если d₁/d₂=0,8; [τ]=1000 кГ/см²; G=8·10⁵ кГ/см² при допускаемом угле закручивания φ на 1 м длины вала – [φ]=0,5°.

Найти главные напряжения и напряжения у поверхности по площадке, наклоненной к σ₁ на угол α=30°.

Дано: M₁=600 кГ·м, М₃=600 кГ·м, М₄=400 кГ·м (рисунок 10, а); β= d₁/d₂=0,8.

Решение. Из условия равновесия ∑М_Х=0, находим M₂=1600 кГ·м (против часовой стрелки). Строим эпюру крутящих моментов: М_кр=1000 кГ·.

Из условия прочности

 

 

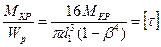
находим, что d₁=9,53 см. Из условия жесткости

 

 

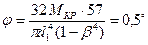
получаем, что d₁=12,2 см.

Принимаем диаметр d₁=12,2 см. Поэтому действительное тангенциальное напряжение на поверхности

 

 

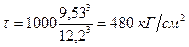
Из круга Мора (рисунок 10, б) находим: σ₁=ОА=τ= 480 кГ/см². Для площадки α=30° определяем (ОК=σ_α=(1/2)480=240 кГ/см²; τ_α=0,87·480=417 кГ/см².

 

 

Глава 3.