ОБЪЕМНОЕ НАПРЯЖЕНОЕ СОСТОЯНИЕ. ТЕОРИИ ПРОЧНОСТИ. БЕЗМОМЕНТНАЯ ТЕОРИЯ ОБОЛОЧЕК.

Методические указания.Изучить расчетные формулы для определения приведенных допускаемых напряжений (по первому главному напряжению) по основным пяти теориям прочности.

По I-й теории наибольших нормальных напряжений получаем расчетную формулу:

 

(10)

по П-й теории наибольших удлинений:

 

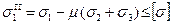
(11)

по III-й теории наибольших касательных напряжений:

 

(12)

по IV-й теории предельного значения энергии формоизменения предельное напряжение равно:

 

(13)

По V-й теории П. П. Баландина в случае основной работы на сжатие для материалов с различным сопротивлением на сжатие (σ_сж) и растяжение (σ_р) квадрат предельного приведенного напряжения будет равен:

 

(14)

где σ₁, σ₂, и σ₃ вносятся в алгебраическом значении, σ_сж и σ_р— предельные сопротивления на сжатие и растяжение материала (для чугуна σ_р≈1/4 σ_сж). В правую и левую части вносятся абсолютные значения σ_сж и σ_р. В случае, когда используется чугун, применяем формулу (14), вводя σ_сж= σ_р:

 

(15)

Откуда для случая чистого сдвига, когда τ=σ₁= - σ₃, получаем:

 

 

Для случая кручения и чистого сдвига, если допускаемое напряжение для чугуна на растяжение равно [σ_р], получаем

 

 

т. е. предельное сопротивление по сдвигу больше, чем предельное сопротивление на растяжение, что отвечает опытным данным. Допускаемое напряжение на сдвиг для чугуна равно 1,16 [σ_р]. Тот же результат дает и условие Губера – Мизеса (13), так как для сдвига σ₁+σ₂+σ₃=0 (в формуле 14). Однако, если σ₁+σ₂+σ₃≠0 уравнение (14) дает отличные от уравнения (13) результаты.

 

Задача № 11. Сравнить первые четыре теории прочности для случая, когда σ₃=1/2σ₁, σ₂=0 (плоское напряженное состояние (рисунок 11, а)). Принять μ=0,25, σ_р=1/2σ_сж. Выразить предельные приведенные напряжения через σ_р и σ_сж.

Решение: По I-й теории (по формуле (10)) σ₁=σ_р=σ_сж. По II-й теории (по формуле (11)):

 

 

 

По III-й теории (по формуле (12))

 

 

Рисунок 11

 

По IV-й теории (по формуле (13))

 

 

Задача № 12.Найти предельное напряжение по σ₁ для случая сжатия чугунного образца, когда σ₁=1/2σ₃ по IV-й и V-й теориям (рисунок 11, б). Выразить σ₃ через σ_сж.

Решение. На основе IV-й теории результат' тот же, что и для задачи № 11: σ₃= 1,155 σ_сж. По V-й теории уравнение (14) принимает вид

откуда σ₃= 1,7 σ_сж

 

Задача № 13. Найти допускаемые напряжения (по σ₁) в случае объемного напряженного состояния, представленного на рисунке 12, применив II-ю и IV-ю теории прочности. Принять μ=0,25.

Ответ: По II-й теории [σ₁] = 1,33[σ], по IV-й теории [σ₁]=2[σ].

 

Задача № 14. Каковы касательные напряжения по любой площадке, параллельной главным направлениям при равномерном растяжении (сжатии), если σ₁=σ₂=σ₃.

Ответ: τ=0, явления сдвига нет.

 

Рисунок 12

 

Задача № 15. Найти толщину цилиндрического сосуда диаметром D=1,2 м, если внутреннее давление р=40 кГ/см², а основное допускаемое напряжение [σ]=2400 кГ/см² (рисунок 13). Применить первую, третью и четвертую теории прочности. По какому сечению возникает σ_max?

 

Рисунок 13

 

Решение. Обозначая меридиональное нормальное напряжение через σ_м, окружное напряжение через σ_ок, из уравнения Лапласа получаем:

 

(16)

где ρ₁ - радиус кривизны меридиональной кривой (в данном случае ρ=∞); ρ₂=радиус кривизны широтного круга (ρ₂=r =D/2); δ-толщина стенки сосуда; ρ - внутреннее давление.

Из условия равновесия отсеченной части получаем

 

(17)

Из уравнения Лапласа имеем

 

(18)

С помощью формулы (17) находим

 

(19)

т. е. меридиональное напряжение в два раза меньше, чем окружное (опасная площадка совмещает образующую цилиндра).

Определяем главные напряжения:

 

 

По I-й теории прочности

 

 

По III-й теории прочности σ₁-σ₃=[σ]; σ₂ - не влияет на условия прочности, δ=1 см.

По IV-й теории прочности (см. задачу №11)

 

 

 

Наиболее экономичное решение позволяет получить IV-я теория прочности.

 

 

Глава 4.