рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Строительство
- /
- ПОПЕРЕЧНЫЙ ИЗГИБ.
Реферат Курсовая Конспект
ПОПЕРЕЧНЫЙ ИЗГИБ.
ПОПЕРЕЧНЫЙ ИЗГИБ. - раздел Строительство, РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОЛИНЕЙНОГО БРУСА. Методические Указания.При Построении Эпюр QX, M...
Методические указания.При построении эпюр Qx, Mx, EIφx= x, EIyx=
x, EIyx= x, использовать дифференциальные зависимости:
x, использовать дифференциальные зависимости:
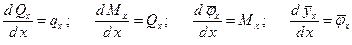
где φx – угол наклона, yx – ордината упругой линии.
Задача № 16.Построить эпюры Qx и Мх и подобрать сечение двутавровой балки в случае, изображенном на рис. 14, а, если [σ] = =1500кГ/см2. Определить величину прогиба посредине балки, если Е=2·106 кГ/см2.
Решение. Определяем реакции А=-2 т, В=-4 т. Строим эпюры Q и М (см. рисунок 14, б). Если Q возрастает (правая половина балки) - эпюра М имеет выпуклость вниз. Там, где Q=0, Mmin=-2·3 + 3 - 1 =-4 тм. По сортаменту при [σ]=1500 кГ/см2 имеем двутавр № 27а с моментом инерции I=5500 см2. Запишем уравнение равенства прогиба на правой опоре (рисунок 14, г):

откуда  0=8,625;
0=8,625;  с=8,625 – 2(33/6)=-0,375 тм3. Найдем величину прогиба посредине балки:
с=8,625 – 2(33/6)=-0,375 тм3. Найдем величину прогиба посредине балки:


Рисунок 14
Задача №17. Построить эпюры Q и М и найти величину прогиба в точке k посредине пролета, подобрав размер сечения двутавровой балки, если [σ]=1970 кГ/см2, E=2·106 кГ/см2 для нагрузки, представленной на рисунке 15, а.
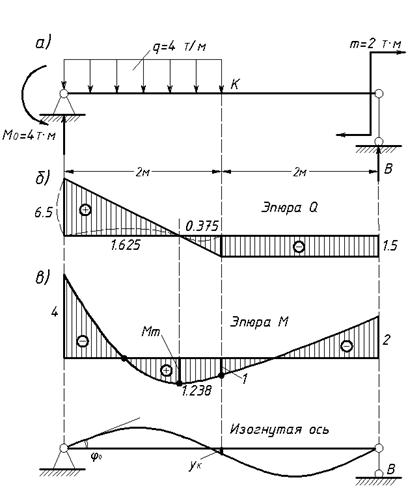
Рисунок 15.
Решение. A=6,5 т, В=1,5 т, Строим эпюры Q и M (см. рисунок 15, б, в). |Mmax|=4 тм, W=203 см3. Итак, следует взять двутавровую балку № 20а (I=2030 см4); EI=2·106·2030=4,06·109; EIφ0=0,67 тм2; EIyk=-1,65 тм3, yk=-0,412 см.
Задача № 18. При действии двух сосредоточенных сил (Р=30 т) построить эпюры Q и М, подобрать сечение двутавровой балки, если [σ]=1550 кГ/см2, и найти направление и величину σmax в опасной точке опасного сечения. Определить здесь τmах (рисунок 16, а).

Рисунок 16.
Решение. Эпюры Q и М даны на рисунке 16, б. Qmax=P=30 т, Мmax=24 тм. Необходимый момент сопротивления W=М/[σ]=1550 см3; берем двутавровую балку с сечением № 50; I=39 290 см4; S0,5=905; Sпол=626 см3. Напряжения в поперечном сечении балки в месте перехода от стенки к полке будут равны: σk=1530; τk=505 кГ/см2.
Найдем главное напряжение (см. рисунок 16, в)


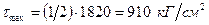
Задача № 19. Построить эпюры Q и М, подобрать сечение двутавровой балки при [σ]=1390 кГ/см2 и определить величину прогиба свободного конца балки, если E=2·106 кГ/см2 (рисунок 17, а).
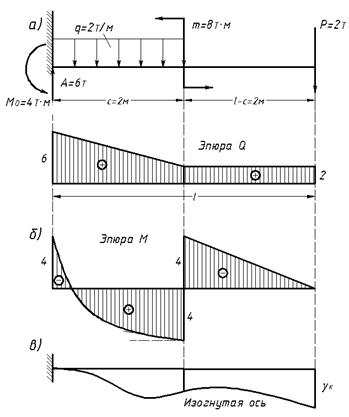
Рисунок 17.
Решение. Найдя реакции А=6 т и М=-4 тм,, строим эпюры Q и М (рисунок 17, б). Необходимый момент сопротивления W=400000/1390=288; берем двутавровую балку с сечением № 24. Тогда I=3460 см4; EI=6,92·109 кГ·см2;
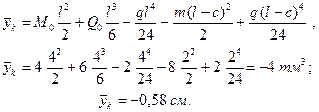
Общий вид изогнутой оси дан на рисунке 17, в.

Рисунок 18.
Задача № 20. Построить эпюры Q и М. Найти Мmax. Подобрать размер сечения двутавровой балки, если [σ]=1420 кГ/см2 (рисунок 18, а).
Ответ. реакции A=1 т; В=-3 т; Mmax=5,25 тм (рисунок 18, б). Следовательно, берем двутавровую балку с сечением № 27.

Рисунок 19.
Задача № 21. Построить эпюры Q и М и найти величину прогиба свободного конца балки, выразив его через EI=const (рисунок 19, а).
Ответ: реакции А=0, Мо=-(ql2/4). Эпюры Q и M даны на рисунке 19, б. Величина наибольшего прогиба
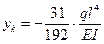
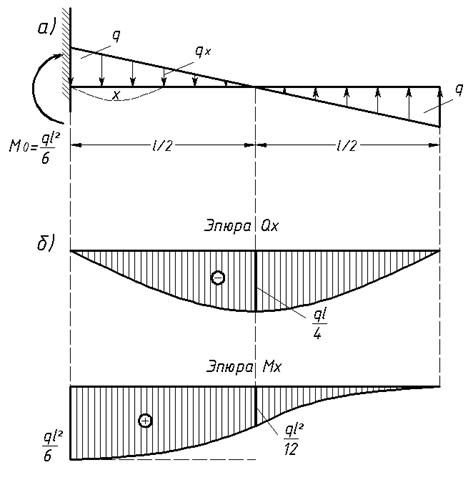
Рисунок 20.
Задача № 22. Построить эпюры Q и М при действии на балку неравномерно распределенной нагрузки (рисунок 20, а).
Ответ: реакции А=0, Мо=ql2/6. Эпюры Q и М изображены на рисунке 20, б. Запишем уравнение интенсивности для qx:
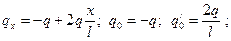
уравнение поперечной силы для Qx:

уравнение изгибающего момента для Mx:

Эти уравнения получены по методу начальных параметров.
Задача № 23. Определить величину прогиба свободного конца консоли ступенчатой балки (рисунок 21, а), если I2=1/6 I1, m=Ра, с=2а. Выразить ее в зависимости от I1.
Решение. Определяем реакции А=В=m/2а. Строим эпюры Q и М (рисунок 21, б). Находим скачки во 2-й и 3-й производных y в месте у правой опоры (N2 и N3 соответственно):
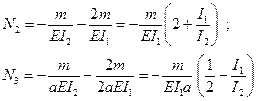
Находим  0=EI1φ0 из условия равенства нулю величины прогиба на правой опоре:
0=EI1φ0 из условия равенства нулю величины прогиба на правой опоре:

откуда EI1φ0=-4/3 ma. Величина прогиба с учетом жесткости в середине пролета равна EI1yc=-3/4 mа2. Для конца консоли по методу учета скачков в производных и приводя к Е11, имеем:
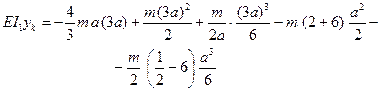
Последние два члена в этом выражении учитывают влияние скачков производных упругой линии. Итак, для ступенчатого бруса получаем EI1yk=-0,167 ma2, а для бруса с постоянным сечением EI1yk=-1,333 ma2.

Рисунок 21.
Глава 5.
– Конец работы –
Эта тема принадлежит разделу:
РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОЛИНЕЙНОГО БРУСА.
На сайте allrefs.net читайте: РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОЛИНЕЙНОГО БРУСА....
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ПОПЕРЕЧНЫЙ ИЗГИБ.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов