рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Строительство
- /
- СЛОЖНОЕ СОПРОТИВЛЕНИЕ.
Реферат Курсовая Конспект
СЛОЖНОЕ СОПРОТИВЛЕНИЕ.
СЛОЖНОЕ СОПРОТИВЛЕНИЕ. - раздел Строительство, РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОЛИНЕЙНОГО БРУСА. МетодическиеУказания. В Данной Главе Решаются Задачи На Косо...
Методическиеуказания. В данной главе решаются задачи на косой изгиб, на внецентренное сжатие, на изгиб и растяжение, на изгиб и кручение, на изгиб кривого бруса и на деформацию толстостенных цилиндров. При косом изгибе сводим задачу к изгибу в двух главных плоскостях, при внецентренном сжатии или растяжении — к изгибу в двух главных плоскостях и действию осевой силы; при этом следует знать формулы для наибольших нормальных напряжений и определять положение нулевой линии. При изгибе и кручении необходимо уметь определять нормальное напряжение при изгибе и касательное напряжение при кручении с тем, чтобы далее уметь определять расчетное напряжение по заданной теории прочности. При изгибе кривого бруса необходимо знать, как определяются положение нейтральной линии и нормальное напряжение. При анализе напряженного состояния толстостенного цилиндра (задача Ляме) —уметь строить эпюры радиальных и тангенциальных нормальных напряжений по толщине цилиндра и определять радиальные перемещения. Необходимо проработать решение задачи о насадке двух цилиндров друг на друга при наличии отклонений в радиальных размерах, применяя выражения для соответствующих радиальных перемещений.
Задача № 28.На балку прямоугольного сечения, защемленную левым концом, действуют вертикальная и горизонтальная силы, каждая величиной Р = 250 кГ. Длина а=2 м; h/b = 2. Найти размеры сечения, если [σ] = 100 кГ/см2 (рисунок 27).
Решение. Наибольшее напряжение будет в точке А, где
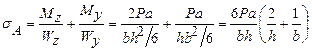
или, учитывая условие прочности и внося h — 2b:
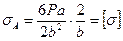
Подставляя Р = 250 кГ, а = 200 cм, получаем
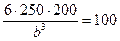
откуда b = 14,42 см. Итак, размеры сечения балки должны быть следующими: b = !5 см, h = 30 см.

Рисунок 27.
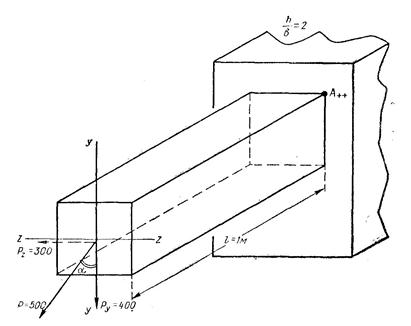
Рисунок 28.
Задача № 29. На свободный конец балки с прямоугольным сечением действует сила Р = 500 кГ под углом α к оси Y (tgα = 0,75; α = 36°52/). Найти напряжения в опасной точке опасного сечения, если длина пролета l= 1 м (рисунок 28). Размеры сечения балки h X Ь = 20 X 10 см, [σ] = 150 кГ/см2.
Решение. Наиболее напряженной будет точка А. Составляющие силы будут: Pz = 300 кГ; Ру = 400 кГ. Найдем напряжение в точке А:
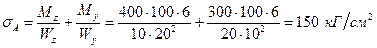
Задача № 30. Определить наибольшие напряжения по основанию фундамента, вес которого G = 14,4 т, если внешняя сила (Р=14 т) приложена с эксцентриситетом е = 0,4 м по главной оси инерции YY (рисунок 29). Размеры сечения hxb = = 2 м X 1 м.
Решение:
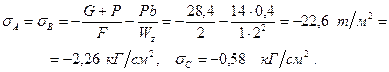
Задача № 31.Определить наибольшие напряжения в крайних точках опасного сечения стального кронштейна, сделанного из выгнутого швеллера №16 (ГОСТ 8240-56). Дано: P=1200 кГ, Wy,1=13,8 см3, z0=1,8 см, F=18,1 см2, Wy,2=35,17 см3 (рисунок 30).
Решение: Применяем формулу внецентренного действия растягивающей силы, считая плечо действия силы Р равным (10+1,8)=11,8 см. Затем для точек 1 и 2 находим:
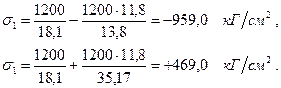
Задача № 32. Определить напряжения в точках 1, 2, 3 и 4 (рисунок 31) основания колонны при действии эксцентрично приложенной силы (Р=1,0 т, эксцентриситеты ez = 5 см, еу=10 см). Сечение колонны 20 X 10 см (рисунок 31, а).
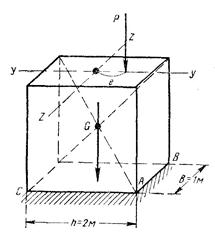
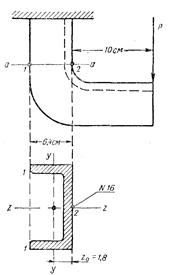
Рисунок 29. Рисунок 30.
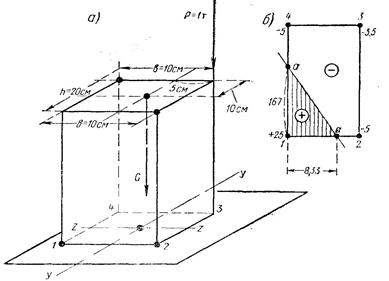
Рисунок 31.
Решение: Находим напряжения от действия силы Р:
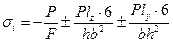
Для точек 1, 2, 3 и 4 соответственно находим:
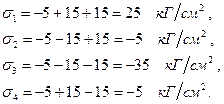
Наиболее напряженной является точка 3. На рисунке 31, б показана нулевая линия напряжений аа.
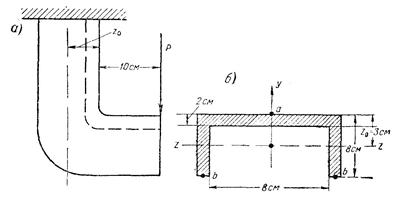
Рисунок 32.
Задача № 33. Чугунный кронштейн швеллерного сечения (рисунок 32) подвергается действию вертикальной силы, приложенной на расстоянии 10 см от полки. Определить допускаемое значение Р, если [σр] = 200 кГ/см2, [σсж] = 800 кГ/см2 (размеры сечения указаны на чертеже).
Решение. Находим положение центра тяжести сечения, z0=3 см, F = 48 см2. Определяем момент инерции Iz= 272 см4, моменты сопротивления для точек а и b: Wa=90,67; Wb = 54,4 см3. Записываем условия прочности:
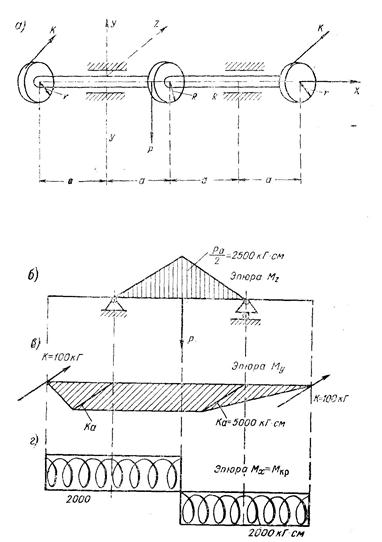
Рисунок 33.
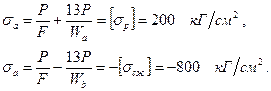
Наименьшее значение находится по первому условию: Р=1220 кГ.
Задача № 34. Подобрать диаметр сплошного вала (рисунок 33), подверженного действию моментов от ременных передач, дающих как горизонтальные, так и вертикальные равнодействующие (К и Р). Учесть наличие изгиба в двух плоскостях и кручения. Применить IV-ю теорию прочности, если Р=100 кГ, R = 40 см, r = 20 см, а = 0,5 м; [σ]=800кГ/см2.
Решение. Из условия равновесия ∑Мx = 0 находим К=100 кГ. Строим эпюры изгибающих Mz, My и крутящего -Мкр моментов. Эти эпюры представлены на рисунке 33, б, в, и г. Приведенный момент по IV-й теории прочности будет равен:
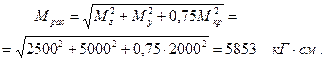
Диаметр определяем, вводя осевой момент сопротивления:
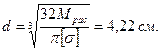
Задача № 35. Определить нормальные напряжения в опасном поперечном сечении кривого бруса 1-2 (рисунок 34), ось которого очерчена по четверти окружности, при действии силы Р = 2 т; R1=25 см; R2 = 15 см; Ro = 20 см; h= 10 см; b = 4 см; М = PR0 = 40 т·см.
Решение. Определяем отношение
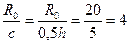
– Конец работы –
Эта тема принадлежит разделу:
РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОЛИНЕЙНОГО БРУСА.
На сайте allrefs.net читайте: РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОЛИНЕЙНОГО БРУСА....
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: СЛОЖНОЕ СОПРОТИВЛЕНИЕ.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов