рефераты конспекты курсовые дипломные лекции шпоры

Раздел Механика
/
Задача 12.2.2.

Реферат Курсовая Конспект

Выберите учебное заведение

Задача 12.2.2.

Задача 12.2.2. - раздел Механика, Федеральное агентство по образованию Плотность Распределения Непрерывной Случайной Величины ...

Плотность распределения непрерывной случайной величины 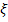имеет вид:

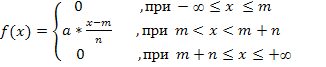
Найти:

а) параметр а; б) функцию распределения ;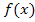

в) вероятность попадания случайной величины 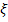в интервал

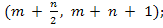
г) математическое ожидание 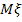и дисперсию .
Построить графики функций и .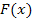

Решение:

Плотность распределения непрерывной случайной величины 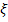при m = 6, n = 1примет вид:

Используя свойства функций плотности и распределения, найдем:

а) параметр а;
б) функцию распределения;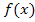
в) вероятность попадания случайной величины в интервал

(m + 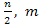+ n + 1) = (6,5; 8);

г) математическое ожидание 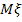и дисперсию D.

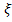а) Если все значения случайной величины принадлежат [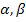], параметр а находиться из условия (условие нормировки)

Вычислим :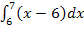

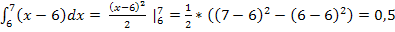
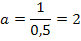
Отсюда, функция плотности распределения:

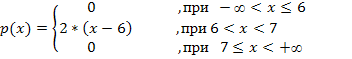
б) Функцию распределения находим по формуле:

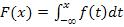При:

При :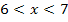

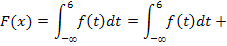
При: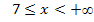

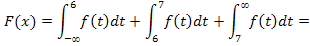
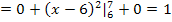
Функция распределения примет вид:

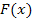
в) Вероятность попадания случайной величины в интервал (6,5; 8) можно вычислить двумя способами:

1 способ:

. В условиях задачи

P (6,5 <

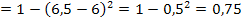
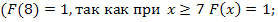
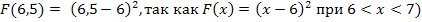
2 способ:

По формуле:

; a=6,5; b=8

Тогда:

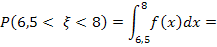
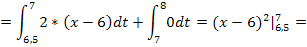
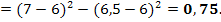
г) Математическое ожидание и дисперсия

Математическое ожидание находим по формуле:

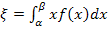
Дисперсию вычисляем по формуле:

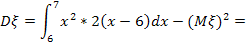
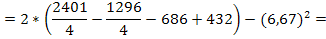
Строим графики и :

Развернуть

Открыть в широком формате

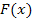– Конец работы –

Эта тема принадлежит разделу:

Федеральное агентство по образованию

Федеральное агентство по образованию... Санкт Петербургский государственный университет сервиса и... Кафедра quot Прикладная математика и эконометрика quot...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Задача 12.2.2.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в ученических тетрадях в клетку. На обложке необходимо указать: название института Академии; название кафедры (математики и математических ме

Случайные события.
12.1.1. В ящике находятся одинаковых пар перчаток черного цвета и

Случайные величины.
12.2.1. Закон распределения дискретной случайной величины имеет вид:

Численная обработка данных одномерной выборки.
Выборка объемом и

Общие указания.
1. Решение задач этой темы основано на простейшей модели теории вероятностей для вычисления вероятностей, в которой , называют «Классической схемой», а определение вероятности – формулой класс

Задача 12.1.1.
В ящике находятся (m+3) одинаковых пар перчаток черного цвета и (n+2) одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пар

Задача 12.1.2.
В урне находится три шара белого цвета и (n+1) шаров черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется:

Способ.
Как отмечали, что извлечение шаров с возвратом – независимые испытания и в каждом испытании вероятность события В – извлечен белый шар, постоянна (и при n=3

Задача 12.2.1.
В урне находиться (m+2) белых и (n+2) черных шара. Три шара последовательно извлекаются без возвращения их в урну. Найти вероятность того, что третий по счету шар окажется белым.

Общие указания.
Кроме случайных событий и вероятностей их появления, в теории вероятностей изучают случайные величины – величины, которые в результате испытания принимают те или иные значения в зависимости от исхо

Задача 12.2.1.
Закон распределения дискретной случайной величины имеет вид: -2

Задача 12.2.3.
Случайные величины имеют геометрическое, биноминальное и пуассоновское распределения соотве

Численная обработка данных одномерной выборки.
Выборка X объемом N = 100 измерений задана таблицей:

Задача 13.1.1.
Построить полигон относительных частот . Решение: Вычислим по фо

Задача 13.1.2.
Вычислить среднее выборочное , выборочную дисперсию

Задача 13.1.3.
По критерию проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости