рефераты конспекты курсовые дипломные лекции шпоры

Раздел Механика
/
Задача 12.2.3.

Реферат Курсовая Конспект

Выберите учебное заведение

Задача 12.2.3.

Задача 12.2.3. - раздел Механика, Федеральное агентство по образованию Случайные Величины ...

Случайные величины 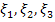имеют геометрическое, биноминальное и пуассоновское распределения соответственно. Найти вероятности
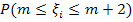, если математические ожидания 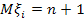, а дисперсия .

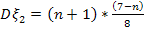Решение:

По условию задачи при значениях параметров m=3, n=3, надо найти
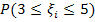, если , ,

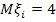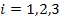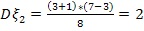
1.Случайная величина 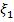имеет геометрическое распределения, если её возможные значения 1,2,3,4…. , а вероятности этих значений
.

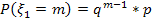Известно, что ; тогда ;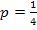
так как 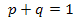, тогда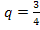

Вычислим:

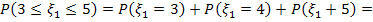
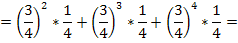
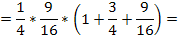
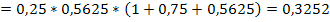
2. Случайная величина 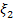имеет биноминальное распределение, если она принимает значения 0,1,2,3… с вероятностями:

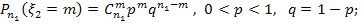
Известно, что:

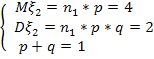тогда, решая эту систему получим:

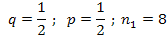
Вычислим:

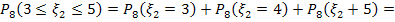
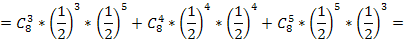
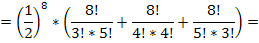
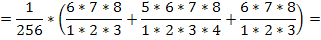
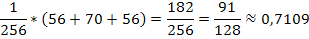
3. Случайная величина 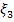имеет распределение Пуассона, если ее возможные значения 0,1,2…, а соответствующие вероятности вычисляются по формуле:

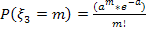, где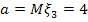

Тогда:

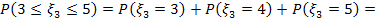
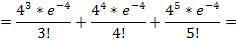
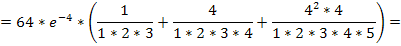
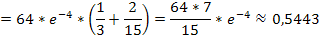
Задача 12.2.4.

Случайные величины 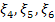имеют равномерное, показательное и нормальное распределения соответственно. Найти вероятности

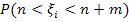, если у этих случайных величин математические

ожидания и среднее квадратические отклонения равны m.

Решение:

Пусть n=2, m=5. Тогда 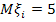, 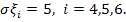Надо найти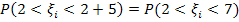

1. Для равномерно распределенной на отрезке [a,b] случайной величины функция плотности имеет вид.

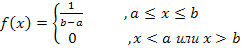
Математическое ожидание вычисляется по формуле:

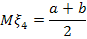
Дисперсия:

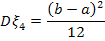
Отсюда, среднее квадратическое отклонение (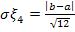

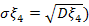
По условию задачи имеем:

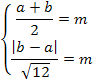
При 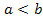эта система равносильна системе:

,

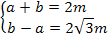решая которую, получаем:

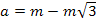
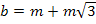
Отсюда:
.

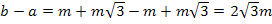Значит, функция плотности имеет вид:

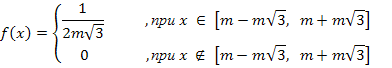
Найдем вероятность 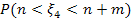по формуле попадания значений случайной величины с функцией плотности 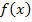в :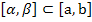

.

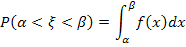
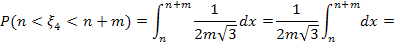
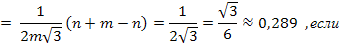
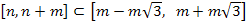Если включение не выполняется, то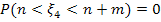

При 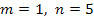получаем, что

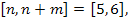
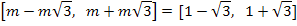
и 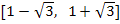вне 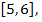т.е. на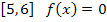

Тогда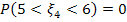

2. Непрерывная случайная величина 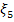имеет показательное распределение, если ее плотность вероятности:

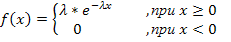
где 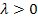параметр распределения,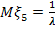

Функция распределения показательного распределения имеет вид:

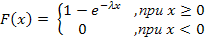
Известно, что 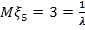, отсюда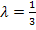

Тогда:

Развернуть

Открыть в широком формате

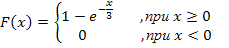
– Конец работы –

Эта тема принадлежит разделу:

Федеральное агентство по образованию

Федеральное агентство по образованию... Санкт Петербургский государственный университет сервиса и... Кафедра quot Прикладная математика и эконометрика quot...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Задача 12.2.3.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Требования к оформлению контрольных работ
1. Контрольные работы следует выполнять в ученических тетрадях в клетку. На обложке необходимо указать: название института Академии; название кафедры (математики и математических ме

Случайные события.
12.1.1. В ящике находятся одинаковых пар перчаток черного цвета и

Случайные величины.
12.2.1. Закон распределения дискретной случайной величины имеет вид:

Численная обработка данных одномерной выборки.
Выборка объемом и

Общие указания.
1. Решение задач этой темы основано на простейшей модели теории вероятностей для вычисления вероятностей, в которой , называют «Классической схемой», а определение вероятности – формулой класс

Задача 12.1.1.
В ящике находятся (m+3) одинаковых пар перчаток черного цвета и (n+2) одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пар

Задача 12.1.2.
В урне находится три шара белого цвета и (n+1) шаров черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется:

Способ.
Как отмечали, что извлечение шаров с возвратом – независимые испытания и в каждом испытании вероятность события В – извлечен белый шар, постоянна (и при n=3

Задача 12.2.1.
В урне находиться (m+2) белых и (n+2) черных шара. Три шара последовательно извлекаются без возвращения их в урну. Найти вероятность того, что третий по счету шар окажется белым.

Общие указания.
Кроме случайных событий и вероятностей их появления, в теории вероятностей изучают случайные величины – величины, которые в результате испытания принимают те или иные значения в зависимости от исхо

Задача 12.2.1.
Закон распределения дискретной случайной величины имеет вид: -2

Задача 12.2.2.
Плотность распределения непрерывной случайной величины имеет вид:

Численная обработка данных одномерной выборки.
Выборка X объемом N = 100 измерений задана таблицей:

Задача 13.1.1.
Построить полигон относительных частот . Решение: Вычислим по фо

Задача 13.1.2.
Вычислить среднее выборочное , выборочную дисперсию

Задача 13.1.3.
По критерию проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости