рефераты конспекты курсовые дипломные лекции шпоры

Реферат Курсовая Конспект

Задача 12.2.1.

Задача 12.2.1. - раздел Механика, Федеральное агентство по образованию В Урне Находиться (M+2) Белых И (N+2) Черных Шара. Три Шара Пос...

В урне находиться (m+2) белых и (n+2) черных шара. Три шара последовательно извлекаются без возвращения их в урну. Найти вероятность того, что третий по счету шар окажется белым.

 

Решение:

Пусть А – случайное событие, что третий по счету извлеченный шар белый. Это событие можно представить как сумму четырех несовместных событий:

 

– первый, второй и третий шары белые;

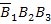- первый шар черный, второй и третий белые;

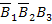- первый и второй шары черные, третий – белый;

- первый и третий шары белые, второй – черный.

 

А = + + +

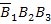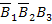По формуле суммы несовместных событий:

 

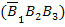P(А) = P +P +P +P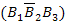

 

В каждом слагаемом события между собой зависимы, так как шары после извлечения в урну не возвращаются. Пусть m=5, n=2. Тогда в урне
m + n = 5 + 2 = 7 белых шаров и n + 2 = 2 + 2 = 4 черных шаров. Всего шаров 7+4=11. Будем использовать классическое определение вероятности и теорему умножения для зависимых событий:


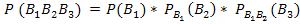
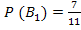(всего шаров 11, 7 – белых)

(после извлечения первого белого шара в урне остается 10 шаров, среди которых 6 белых)

(после извлечения первого и второго белых шаров, в урне осталось 9 шаров, среди которых 5 белых)

Таким образом имеем:

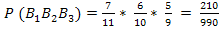
Аналогично рассуждая, получим:

 

 

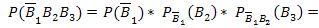
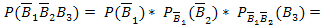
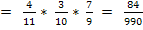
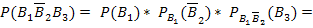
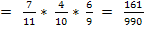
Тема 12.2. Случайные величины.

Развернуть
Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Федеральное агентство по образованию

Федеральное агентство по образованию... Санкт Петербургский государственный университет сервиса и... Кафедра quot Прикладная математика и эконометрика quot...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Задача 12.2.1.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Требования к оформлению контрольных работ
  1. Контрольные работы следует выполнять в ученических тетрадях в клетку. На обложке необходимо указать: название института Академии; название кафедры (математики и математических ме

Случайные события.
12.1.1. В ящике находятся одинаковых пар перчаток черного цвета и

Случайные величины.
12.2.1. Закон распределения дискретной случайной величины имеет вид:  

Численная обработка данных одномерной выборки.
Выборка объемом и

Общие указания.
1. Решение задач этой темы основано на простейшей модели теории вероятностей для вычисления вероятностей, в которой , называют «Классической схемой», а определение вероятности – формулой класс

Задача 12.1.1.
В ящике находятся (m+3) одинаковых пар перчаток черного цвета и (n+2) одинаковых пар перчаток бежевого цвета. Найти вероятность того, что две наудачу извлеченные перчатки образуют пар

Задача 12.1.2.
В урне находится три шара белого цвета и (n+1) шаров черного цвета. Шар наудачу извлекается и возвращается в урну три раза. Найти вероятность того, что среди извлеченных шаров окажется:

Способ.
Как отмечали, что извлечение шаров с возвратом – независимые испытания и в каждом испытании вероятность события В – извлечен белый шар, постоянна (и при n=3

Общие указания.
Кроме случайных событий и вероятностей их появления, в теории вероятностей изучают случайные величины – величины, которые в результате испытания принимают те или иные значения в зависимости от исхо

Задача 12.2.1.
Закон распределения дискретной случайной величины имеет вид: -2

Задача 12.2.2.
Плотность распределения непрерывной случайной величины имеет вид:

Задача 12.2.3.
  Случайные величины имеют геометрическое, биноминальное и пуассоновское распределения соотве

Численная обработка данных одномерной выборки.
Выборка X объемом N = 100 измерений задана таблицей:    

Задача 13.1.1.
Построить полигон относительных частот . Решение: Вычислим по фо

Задача 13.1.2.
Вычислить среднее выборочное , выборочную дисперсию

Задача 13.1.3.
По критерию проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости

Хотите получать на электронную почту самые свежие новости?
Education Insider Sample
Подпишитесь на Нашу рассылку
Наша политика приватности обеспечивает 100% безопасность и анонимность Ваших E-Mail
Реклама
Соответствующий теме материал
  • Похожее
  • Популярное
  • Облако тегов
  • Здесь
  • Временно
  • Пусто
Теги