рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Сложные суждения и условия их истинности
Реферат Курсовая Конспект
Сложные суждения и условия их истинности
Сложные суждения и условия их истинности - раздел Механика, Логика как наука о мышлении Сложные Суждения - Такие, Которые Состоят Из Простых Суждений...
Сложные суждения - такие, которые состоят из простых суждений, связанных между собой логическими союзами (связками): «не», «и», «или», «если.., то», «если, и только если.., то».
Логические связки, или союзы, выражают логические операции.
Отрицание - логическая операция, в результате которой из данного суждения (р) получается новое суждение (не- р), называемое отрицанием исходного суждения.
Конъюнкция - логическая операция, соединяющая два или более высказывания при помощи союза «и» (p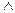 q).
q).
Дизъюнкция - логическая операция, соединяющая два или более высказывания при помощи союза «или» (р или q; символически p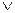 q). Союз «или» употребляется в естественном языке в двух значениях - соединительно-разделительном и исключающее - разделительном.
q). Союз «или» употребляется в естественном языке в двух значениях - соединительно-разделительном и исключающее - разделительном.
Слабая дизъюнкция - логическая операция, соединяющая высказывания при помощи союза «или», употребленного в соединительно-разделительном значении, т. е. когда входящие в сложное суждение составляющие суждения не исключают друг друга. Например, в суждении «Н. - преступник или М. - преступник» утверждается, что преступником может быть Н. или М., или оба вместе (символически: p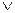 q).
q).
Строгая дизъюнкция - логическая операция, соединяющая высказывания при помощи союза «или», употребленного в исключающем смысле: либо Н. преступник, либо М. - преступник, но не оба вместе (либо p, либо q; символически: p q).
q).
Импликация - логическая операция, соединяющая высказывания при помощи союза «если.., то» (символически р → q).
Эквивалентность - логическая операция, позволяющая из двух высказываний р и q получить новое высказывание: р эквивалентно q (символически р ≡ q, или р ↔ q).
В зависимости от того, какие логические союзы используются при образовании сложных суждений, последние делятся на следующие виды: отрицательные, соединительные, разделительные, условные и эквивалентные суждения.
Все эти сложные суждения могут быть истинными и ложными. Но их истинность (ложность) зависит от истинности (ложности) простых суждений и смысла логических союзов, с помощью которых они образуются. Точный смысл логических союзов определяется с помощью так называемых таблиц истинности. Рассмотрим каждый их этих видов суждений.
Отрицание - суждение, образованное с помощью союза «не». Например, имеем суждение: «Человек совершил преступление» (р). Его отрицанием будет: «Неверно, что человек совершил преступление» p). Смысл отрицания состоит в следующем: если какое-то суждение (р) - истинно, то его отрицание (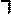 p) будет ложным. Если p - ложно, то его отрицание
p) будет ложным. Если p - ложно, то его отрицание  p - истинно. Союз «не» меняет значение истинности на противоположное.
p - истинно. Союз «не» меняет значение истинности на противоположное.
Конъюнктивное (соединительное) суждение - суждение, которое включает в качестве составных частей другие суждения, объединяемые союзом «и». Например: «Мы поедем в Санкт-Петербург и посетим Русский музей». В этом суждении выражается уверенность, что произойдут оба эти события. Схематично: «р q».
q».
В естественном языке, в том числе и в правовых текстах, конъюнкция может быть выражена словами «и», «а», «но», «также», «хотя», «однако», «несмотря на», «вместе с тем» и др.
Истинность конъюнкции зависит от истинности (ложности) простых суждений «р и q» и от смысла логического союза - конъюнкции. Если мы имеем два простых суждения, а каждое из них может иметь два значения («истина» и «ложь»), то всего должны рассмотреть четыре разных случая: когда оба суждения истинны; когда первое истинно, а второе ложно; когда первое ложно, а второе истинно и когда оба ложны.
Конъюнктивное суждение приобретает значение истинности («истины») лишь когда оба простых суждения истинны, так как союз «и» соединяет суждения, события в которых происходят одновременно. Во втором и в третьем случаях конъюнкция является ложной в силу ложности одного из ее членов; в четвертом ложность конъюнкции определяется ложностью обоих ее членов.
Таким образом, сколько бы членов p, q, r... ни включало сложное конъюнктивное суждение, достаточно обнаружить среди них хотя бы один ложный член, чтобы считать конъюнкцию ложной.
Дизъюнктивное (разделительное) суждение - это суждение, которое включает в качестве составных частей суждения, объединяемые союзами «или», «либо». Например: «Договор купли-продажи может быть заключен в устной или письменной форме» (здесь наличие в предикате двух признаков указывает на сложный характер суждения: его можно разложить на два простых: «Договор купли-продажи может быть заключен в устной форме» и «Договор купли-продажи может быть заключен в письменной форме»).
В естественном языке дизъюнктивные суждения выражаются, как правило, с помощью союзов «или», «либо», «или... или», «либо... либо».
Слабо-разделительное суждение, или суждение со слабой дизъюнкцией - суждение, в котором союз «или» имеет соединительно-разделительное значение. Оно может быть истинным в трех случаях: когда истинны оба суждения; когда р - истинно, a q - ложно; когда р - ложно, a q - истинно. Дизъюнкция считается ложной при ложности всех ее членов.
Строго-разделительное суждение, или суждение с сильной дизъюнкцией - суждение, в котором союз «или» имеет исключающе-раз-делительное значение. Например: «Либо Н. - убийца, либо М. -убийца», «Вина может быть умышленной или неосторожной» (символично: р q). Члены сильной дизъюнкции не могут быть одновременно истинными и ложными.
q). Члены сильной дизъюнкции не могут быть одновременно истинными и ложными.
Суждение с сильной дизъюнкцией может быть истинным только в двух случаях: когда первое суждение истинно (Н. - убийца), а второе - ложно (М. - не убийца) или когда первое ложно, а второе истинно. Оно будет ложным, если входящие в него простые суждения одновременно истинны или одновременно ложны.
Импликативное (условное) суждение - это сложное суждение, образованное из простых суждений с помощью логического союза «если.., то». Например: «Если человек совершил преступление, то он должен быть наказан». При этом первое суждение (начинающееся словом «если») называется основанием, а второе (начинающееся словом «то») - следствием (заключением). Символически: р → q.
Форму условной связи могут принимать различные виды объективных зависимостей: причинные, пространственно-временные, логические и другие. Пример причинной связи: «Если нагреть воду до 100 градусов при нормальном давлении, то она закипит». Пример логической связи: «Если человек женат, то он не холост» или «Если всякое преступление наказуемо, а кража преступна, то она наказуема».
В естественном языке союз «если.., то» может употребляться для сопоставления. Например: «Если в 1940 г. население Москвы составляло 3 млн, то в 2000 г. оно составляет около 10 млн. человек». Условная связь выражается в языке и такими союзами, как «там.., где», «тогда.., когда», «постольку.., поскольку» и др. В правовых нормах в форме условных суждений фиксируются не только причинные, временные, пространственные и другие объективные связи между явлениями, но и деятельно-волевые предписания в форме разрешения, обязывания или запрета совершать определенные действия.
В науке и юридической практике очень важно проводить различие между необходимыми и достаточными условиями наступления какого-либо факта, события, отражаемого в условном суждении.
Условия являются необходимыми, если без их выполнения данное событие никогда не наступает. Например, для того чтобы какое-то число делилось на 6, необходимо, чтобы оно делилось на 2.
Условия являются достаточными, если при их выполнении всегда наступает данное событие. Например, для того чтобы какое-то число делилось на 2, достаточно, чтобы оно делилось на 6.
Необходимые условия не всегда бывают достаточными, а достаточные - необходимыми. Но встречаются и такие условия, которые являются необходимыми достаточными. Например, делимость числа на 2 – необходимое, но недостаточное условие для того, чтобы число делилось на 6. Делимость числа на 6 - достаточное, но необходимое условие для того, чтобы число делилось на 2. Делимость числа на 2 и на 3 - необходимое и достаточное условие для его делимости на 6.
Для определения истинности импликации (р → q) сравним ее с какой-либо деятельностью, в которой посылки (условия) представляют собой как бы материал, сырье для умозаключения, а заключение - готовую продукцию. Очевидно, каждый согласится считать деятельность хорошей (доброкачественной), если посредством ее добротный материал превращается в добротную продукцию. Сапожник хорошо шьет сапоги, если он из хорошего материала - кожи - всегда шьет хорошие сапоги. То же можно сказать и об условном суждении. Переход от посылок к заключению является хорошим (правильным), если он из «хороших» (истинных) посылок всегда дает «хорошие» (истинные) заключения. Другими словами, если р - истинно и q - истинно, то импликация истинна. Если же посылки истинны (р истинно), а заключение (q) ложно, то импликация ложна (по аналогии с действиями сапожника, который испортил хороший материал). Если р ложно, a q истинно, то импликация истинна (вполне возможна ситуация, когда сапожник из плохого материала шьет хорошие сапоги). Если р ложно и q ложно, то импликация истинна, так как эта ситуация также допустима (из плохого материала трудно сшить хорошие сапоги). Итак, импликация истинна во всех случаях, кроме одного - когда истинно основание и ложно следствие.
Эквивалентность - суждение, образованное из простых суждений с помощью союза «тогда, и только тогда, когда». В этих суждениях выражается взаимная обусловленность явлений, событий. Например: «Если человек награжден орденами и медалями, то лишь в этом случае он имеет право на ношение соответствующих орденских планок». При истинно-функциональном подходе аналогом этих суждений выступают выражения, содержащие прямую и обратную импликацию (двойная импликация). В естественном языке такие суждения выражаются также с помощью союзов «если, и только если.., то», «лишь при условии.., что».
Для определения истинности эквивалентности рассмотрим суждение: «Любое деяние следует рассматривать как преступное в том, и только в том, случае, если оно общественно опасно и противоправно» (схематично «р ↔ q»). Истинность р достаточна для признания истинным q и, наоборот, истинность q достаточна для признания истинным p. Эквивалентность истинна только тогда, когда составляющие его простые суждения либо одновременно истинны, либо одновременно ложны.
Для каждой логической связки можно построить таблицы истинности.
Их можно объединить в одну таблицу истинности.
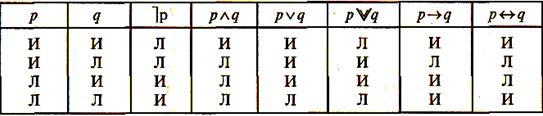
Зная структуру сложного суждения и смысл логических союзов, можно установить истинность (ложность) любого сложного суждения.
В практике обычных рассуждений указанные виды сложных суждений используются как самостоятельно, так и в сочетаниях. Такие комбинированные высказывания часто встречаются в юридических контекстах при описании сложных нормативных предписаний, определении правовых понятий, описании составов преступлений и гражданских правоотношений.
Отрицанием сложного суждения является такое преобразование его структуры, в результате которого из исходного ложного суждения получается истинное (и наоборот).
Отрицание отрицания равно утверждению:  (
(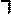 p) = р.
p) = р.
Отрицание конъюнкции: 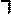 (р
(р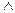 q) =
q) = 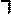 p
p 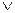
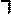 q.
q.
Отрицание дизъюнкции: 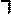 (р
(р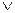 q) =
q) = 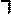 p
p 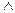
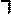 q..
q..
Отрицание импликации: 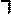 (р → q) =
(р → q) = 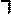 p
p 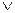 q = р
q = р 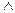
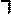 q.
q.
Зная эти правила, можно преобразовывать и упрощать сложные суждения. Возможность эквивалентного выражения одних видов суждений через другие имеет большое практическое применение в автоматике, в кибернетических устройствах, а также при решении других проблем современной науки и техники.
– Конец работы –
Эта тема принадлежит разделу:
Логика как наука о мышлении
Формы рационального познания Логика как наука Основные понятия и проблемы Логика как наука о... Логика и язык Логическая форма Логические законы и... Классическая логика высказываний Язык и табличное построение Понятие закона логики...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Сложные суждения и условия их истинности
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов