Логика как наука о мышлении

ОТВЕТЫ к экзамену

Формы рационального познания. Логика как наука. Основные понятия и проблемы.

Логика как наука о мышлении

Слово «логика» происходит от греческого logos, что означает «мысль», «слово», «разум», «закономерность». В современном языке это слово используется,… 1) для обозначения закономерностей и взаимосвязей между событиями или… 2) для обозначения строгости, последовательности, закономерности процесса мышления; при этом употребляются выражения:…

Логика и язык. Логическая форма. Логические законы и теории.

Язык логики

Наше мышление не сущ-т без языка => понятия не сущ-т без слова. Сужд-я не сущ-т без предлож-я. Умозакл-я нельзя построить без сужд-й.   Поскольку логика изучает формы мышления, а мышление неразрывно связано с языком, постольку логика является также…

Логическая форма и законы мышления

В естественном языке мысли выражаются с помощью слов и словосочетаний, имеют конкретное содержание (то, о чем говорится в них). Например, можно… Чтобы выявить внутреннюю структуру понятий, сравним разные по содержанию… Они отражают разные предметы и различны по своему содержанию. Но есть ли в них что-то общее?

Предложение, суждение, высказывание. Виды сложных высказываний, условия их истинности.

Субъект суждения - это понятие, отражающее предмет мысли, то, о чем мыслится в данном суждении. Обозначается буквой «S». Предикат суждения - это понятие, отражающее признак предмета мысли, то, что… Связка выражает отношение, которое существует в суждении между субъектом и предикатом. Она характеризует…

Сложные суждения и условия их истинности

Сложные суждения - такие, которые состоят из простых суждений, связанных между собой логическими союзами (связками): «не», «и», «или», «если.., то»,… Логические связки, или союзы, выражают логические операции. Отрицание - логическая операция, в результате которой из данного суждения (р) получается новое суждение (не- р),…

Классическая логика высказываний. Язык и табличное построение. Понятие закона логики высказываний.

Язык и табличное построение КЛВ.

изучающая логическую структуру сложных высказываний, отношения между ними и выводы, построенные с учетом этой структуры. При выявлении логических форм контекстов естественного языка

Основные принципы формальной логики. Понятие законов логики

Логика высказываний — это логическая система, которая анализирует процессы рассуждения, опираясь на истинностные характеристики логических связок и… Под высказыванием принято понимать языковое предложение, о котором имеет смысл… В логике высказываний интересуются не содержанием, а истинностью или ложностью высказываний.

Логические отношения между сложными высказываниями.

Несравнимые — это суждения, которые не имеют общих пропозициональных переменных. Сравнимые — это суждения, которые имеют одинаковые пропозиционные переменные… Сложные сравнимые суждения могут быть совместимыми и не совместимыми.

Отношения между сложными суждениями

К независимым относятся суждения, которые не имеют общих составляющих; для них характерны все сочетания истинных значений. Зависимые - это суждения,…

Сложные зависимые суждения могут быть совместимыми и несовместимыми.

К совместимым относятся суждения, которые одновременно могут быть истинными. Как и в случае простых суждений различают три вида совместимости… Эквивалентными являются такие суждения, которые принимают одни и те же… Отношение эквивалентности позволяет выражать одни сложные суждения через другие - конъюнкцию через дизъюнкцию или…

Отношение несовместимости.

Противоположность - отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными. Противоречащими являются суждения, которые одновременно не могут быть ни… Чтобы получить сложное суждение, противоречащее исходному, последнее нужно подвергнуть отрицанию.

Отношение логического следования. Методы проверки правильности рассуждений (табличный и сокращенный).

Логическая форма. Отношение логического следования

Рассмотрим, например, умозаключение, приведенное в предыдущем параграфе. (1)Если ваши книги согласны с Кораном, то они излишни. Если ваши книги не согласны с Кораном, то они вредны. Если ваши книги излишни или вредны, то их следует уничтожить.

Понятие о логике высказываний

Логика высказываний — это логическая система, которая анализирует процессы рассуждения, опираясь на истинностные характеристики логических связок и… Язык логики высказываний включает: алфавит, определение правильно выстроенных… Алфавитidi ики Bbn - k . названий состоит изследующих символов. Символы ,пя |!ыск<1)|,|»аний. р,q , r ...…

А=В

(А->В)л(В-»А) '

Кроме этих прямых правил получения новых строк вывода, в СНВприняты непрямые правила, определяющие стратегию построения вывода. Например, если нужно вывести из посылок формулу вида импликации ( xi —> ( xz —> ...( xn - i -> Хп))), то после выписывания посылок выписываются в качестве допущений все антецеденты заключения, начиная с антецедента главного знака импликации, т.е. xi , • m , хз,..., Xn-i. Г,А->В

Если при этом удастся вывести Хп, то по непрямому правилу -> в , собираем

Г-»А->В

последовательно формулы: ( xn - i -^ Xn ) (при этом исключается допущение Xn-i), (хп-2 —> (Xn-i —> Xn )( xn - r исключается из числа допущений) и т.д., пока не получим требуемое заключение xi -»(хп-2 —>... (Xn-i —> Хп). Это правило построения прямого вывода.

Приведем пример вывода с применением этого правила:

(( pAq )-> r ) |_ ( p -> ( q -> r )

1. (р л q) —> г — посылка
2. р — допущение
3. q — допущение
4. р л q (2, 3. л в)
5. .г(1,4,^„)
6. q -> г(3,5, ^в)(-3)
7. p ^( q ^ r )(2,6, -^.)(-2)

Другое непрямое правило используется для построения косвенного вывода, при котором допущением является отрицание В или отрицание последнего консеквента Хп. Это правило имеет вид —————-———— и говорит о том, что если из каких-то Г—>|А формул (Г) и допущения (А) получено противоречие (В л ТВ), то из этих формул следует ча. Таким образом, если строится косвенный вывод формулы вида (xi —> (х2 —> ...(xn-i —> Хп)...), то после посылок выписываются формулы:

X] 1

допущения

Х2

Xn-i

^п

допущение косвенного доказательства [ДКД]

Затем по правилам вывода получаем следствия из всех имеющихся посылок и допущений до тех пор, пока не получим две противоречащие друг другу формулы'('В и 1В), что свидетельствуе! о несовместимости допущения косвенного доказательства с другими допущениями и посылками. Отсюда делается вывод о его ложности. Тогда в вывод вписывается строка 11 Хп, и тем самым допущение косвенного доказательства исключается. Например, осуществим косвенный вывод: (р —> q ) ("-(1 q —> 1 p ) (

1. p —> q—посылка
2. 1 q — допущение
3. Ирдкд
4. /Р(3,1и)
5. q ( l ,4,->„)
6. а л 1я(5,2,лв)
7. 1 Up (6,3, 1в)(-3)
8. 1p (7, 1и)
9. 1q -> 1p (2,8, ->и)(-2)

Косвенный вывод считается законченным, если в ходе вывода получена какая-то формула и ее отрицание, т е. противоречие. Таким образом, если строится косвенный вывод формулы вида xi —> ( x - i —>..—> Хп), то построчно выписывают все антецеденты от xi до Xn - i в качестве допущений; в последней строчке выписывают отрицание последнего консеквента — 1хп как допущение косвенного вывода По правилам вывода получаем различные следствия из всех имеющихся посылок и допущений. Получение двух противоречащих следствий говорит о ложности допущения косвенного вывода. Па этом основании ДКД отрицается, т.е. получаем двойное отрицание. Снятие двойного отрицания дает формулу Хп.

Основными логическими свойствами системы натурального вывода являются еенепротиворечивостьиполнота.

Непротиворечивостьозначает, что из истинных посылок могут получаться только истинные следствия и если формула выводима из пустого множества посылок, тоона тождественно истинна. Это исключает возможность вывести из пустого множества посылок какую-либо формулу (А) и ее отрицание (1А).

Полнота системыозначает, что дедуктивных ее средств достаточно, чтобы вывести ,из пустого множества посылок любую тождественно истинную формулу.

Логика предикатов является более общей логической системой и включает логику высказываний как свою часть. Она располагает более эффективными логическими средствами для анализа рассуждений в естественном языке.

Виды простых высказываний. Логическая форма и условия истинности простого атрибутивного высказывания.

Состав и виды простых атрибутивных высказываний

Силлогистика – это теория, изучающая логическую структуру простых атрибутивных высказываний, отношения между ними и выводы, построенные с учетом… неуниверсальных одноместных предикатов). Простыми называются высказывания, не содержащие внутри себя пропозициональных связок.

Логическая форма и условия истинности простого атрибутивного высказывания.

Итак, все простые высказывания можно разделить по двум основаниям: качественной характеристике высказывания и местности его логического сказуемого… Атрибутивные высказывания, логическим подлежащим которых является единичный… Атрибутивные высказывания, логическим подлежащим которых является общий термин, называются множественными.

Отношения между простыми атрибутивными высказываниями, методы их установления.

Простые суждения

Сравнимыми являются суждения с одинаковыми субъектами и предикатами и различающиеся связкой или квантором. Для иллюстрации отношений между простыми суждениями используется логический…

Отношения между атрибутивными высказываниями

что не всегда отражает их действительное отношение друг к другу. Силлогистика в этом смысле является более тонким инструментом рассуждения – она помогает… логические отношения между простыми атрибутивными высказываниями с учетом их

Язык и семантика силлогистики.

Язык силлогистики предназначен для того, чтобы выражать состав, структуру и вид атрибутивных высказываний. Его алфавит включает в себя:   1) Переменные для терминов – S, P, М, …

Непосредственные умозаключения (обращение, превращение, противопоставление субъекту, предикату). Умозаключения по логическому квадрату.

Непосредственными называются умозаключения, в которых вывод делается из од-

ной посылки. Несмотря на тривиальность, в практике аргументации таким выводам от-

водится очень важная роль. Они служат для того, чтобы быстро и правильно отрицать,

ослабить или переформулировать исходное высказывание.

А) Умозаключения по логическому квадрату.

влять ослабление и отрицание атрибутивных высказываний. Ослабление представляет собой переход от общего высказывания к частному с… же качеством (вывод по вертикали логического квадрата):

В) Обращение атрибутивных высказываний.

заключения совпадает с предикатом посылки, а предикат заключения – с субъектом по- сылки. Другими словами, вывод делается по схеме: При обращении атрибутивных высказываний надо соблюдать следующие правила:

С) Превращение атрибутивных высказываний.

Превращение (обверсия) – это непосредственное умозаключение, в котором субъ-

ект заключения совпадает с субъектом посылки, а предикат заключения является терми-

ном, противоречащим предикату посылки. Вывод делается по схеме:

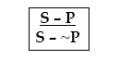
Простой категорический силлогизм (состав, фигуры, модусы). Общие правила силлогизма.

сылки. В таком расширительном смысле силлогизмами являются, например, умозаклю- чения типа modus ponens, modus tollens и т.д., рассмотренные ранее. Простой категорический силлогизм – это умозаключение, в котором от наличия

Правила фигур

(2) Меньшая посылка должна быть утвердительной. 2 фигура:(1) Большая посылка должна быть общей. (2) Одна из посылок должна быть отрицательной.

Общие правила силлогизма

2) Если термин распределен в заключении, он должен быть распределен и в посылке. 3) По крайней мере одна из посылок должна быть утвердительным суждением. 4) Если обе посылки утвердительные, то и заключение должно быть утвердительным.

Методы проверки простого категорического силлогизма. Алгоритм восстановления энтимемы в простой категорический силлогизм.

Простой категорический силлогизм. Структура категорического силлогизма. Способы проверки правильности категорических силлогизмов.

простой категорический силлогизм – дедуктивное умозаключение, в котором из двух категорических посылок (суждений), связанных средним термином (при… Все люди (М) дышат кислородом (Р) Р кислородом дышу S Я

Понятие энтимемы, восстановления силлогизма - основные этапы

Силлогизм, в котором выпущена (не выражена явно) какая-нибудь из его частей (посылка или заключение), называется сокращённым силлогизмом или… Сокращёнными (энтимематическими) могут быть и умозаключения логики суждений.… Энтимема – это умозаключение, в котором пропущена одна из посылок или заключение.

Энтимемы и полисиллогизмы

тором пропущена одна из посылок или заключение. В практике аргументации энтимемы используются довольно часто. Например, для … того, чтобы риторически выделить заключение силлогизма, его иногда пропускают, за-

Понятие как форма рационального познания. Общая характеристика понятий. Закон обратного отношения между содержанием и объемом.

Понятие как основная форма рационального познания. При рассмотрении чувственного познания, то есть познания, включенного в материально-предметную деятельность, была показана его зависимость от языка, от понятийного мышления. Что же такое понятия, как они формируются? В самом общем виде ответ таков.

В ходе физического воздействия на конкретные предметы и явления, в ходе их использования и преобразования, в процессе создания и изменения общественных отношений человечество приобретает многообразные знания об отношениях. Выявляются отношения между различными типами и видами материальных объектов и процессов, между различными свойствами объектов и т.д. Отношения вещей, явлений, процессов многообразны и соответственно многоразличны знания об отношениях. Это могут быть, например, знания об отношениях между свойствами железа, из которого делается топор, и дерева, которое топор может разрубить. Но это могут быть и более сложные знания отношений между массой и ускорением тела, отношений между элементарными частицами внутри атома и т.п.

Поскольку знание направлено на выявление отношений между свойствами предметов, между самими предметами и процессами, в которые они включены, данные отношения становятся объектами познания. Но что это означает для понимания процесса познания, и в частности для понимания механизмов возникновения понятий и их роли в познании?

Уже в обыденной практической жизни мы постоянно имеем дело с отдельными конкретными предметами, которые существуют реально и могут быть непосредственно восприняты при помощи зрения, слуха, осязания. Но при этом мы обязательно выявляем отношения между предметами, а также фиксируем наше отношение к ним, что, например, видно в следующих простейших фразах: "Это дом", "этот дом красив", "роза красная" и т.д. Слова "дом", "красивый", "красная" могут быть отнесены не только к данному конкретному отдельному объекту, который мы непосредственно имеем в виду. Слово "дом" может быть отнесено ко всем весьма непохожим друг на друга зданиям, служащим человеку в качестве жилья. Слова "красивый", "красный" также могут быть отнесены к самым различным предметам, различным классам объектов: ведь красивы не только дома, красны не только розы.

Данные слова уже выражают и отражают отношения между конкретными предметами и явлениями, причем отражают их в обобщенной форме. Когда мы их употребляем, мы имеем в виду некоторые определенные общие свойства, характерные признаки различных предметов и явлении, во многих других измерениях весьма отличных друг от друга. Именно объективная общность свойств становится главным объектом познания. При этом процесс познания развертывается следующим образом: прежде всего мы опираемся на изучение реальных, конкретных предметов как материальных объектов, их действительных, объективно существующих качеств и признаков. Но одновременно происходит активный познавательный процесс: человек целенаправленно сопоставляет разные предметы, которые отнюдь не всегда непосредственно воздействуют друг на друга. Выполняя определенное действие с данными объектами и преследуя ту или иную практическую цель, человек сравнивает их, уподобляет друг другу в каком-либо определенном отношении, оставляя в стороне те отношения и связи, которые его в данный момент и в данном аспекте не интересуют. Человек как бы "рассекает" мыслью реальную целостность конкретного предмета, который всегда включен в самые различные отношения с другими предметами и признаками и потому потенциально представляет собой совокупность самых разнообразных свойств и признаков.

Человек при помощи своей мысли выделяет, как бы обособляет от целостных конкретных предметов такие отношения, которые объективно, сами по себе, и в качестве каких-то особых предметов не существуют. Но они оказываются важными для жизни и деятельности человека и человечества, а поэтому становятся специальными объектами его познавательной деятельности. Эти объекты, выделенные и познанные человеком, выражаются и фиксируются в словах-понятиях, подобных словам "дом", "человек", "красное", "красота" и т.д.

Например, красная роза и красная ткань - предметы во многих отношениях различные. Но когда человека интересует их цвет, он отвлекается от других свойств данных предметов. Он сравнивает эти предметы с точки зрения их цвета (при этом он нередко отвлекается и от оттенков цвета, которые тоже могут быть весьма различными). Объективные связи, отношения данных предметов, воплощенные в общность их цвета, фиксируются и отражаются в слове-понятии "красное".

Процессы, в ходе которых постепенно и последовательно образуются понятия, отражающие общие свойства предметов и явлений окружающего мира, измеряются многими столетиями и уходят в глубь веков. Прежде чем знание о тех или иных отношениях приобретает обобщенную форму и благодаря этому приобретает понятийное выражение, должны миллиарды раз осуществляться процессы сопоставления, сравнения, различения, мысленного "рассечения" и физического видоизменения объектов. Должны остаться в стороне все моменты, несущественные, второстепенные для данного отношения, для данной связи. В процессе человеческой деятельности знания должны быть освобождены и от чисто личных, индивидуальных моментов (чувства, переживания конкретных субъектов, их сугубо индивидуальные цели). Знание должно приобрести обобщенную форму и в том смысле, что в нем должны найти выражение общие объективные отношения, и в том смысле, что оно так или иначе должно приобрести объективное значение для множества людей. В этом случае результатами практической деятельности становятся не только конкретные предметы и явления, вновь созданные или преобразованные, но также и понятия, возникшие в ходе этого процесса и от него на данной стадии неотделимые. Затем созданные в ходе практической деятельности понятия становятся важным компонентом и формой этой деятельности. В последующих процессах использования они проверяются, уточняются и видоизменяются благодаря постоянному сопоставлению с конкретными объектами и отношениями, принадлежащими к данному типу.

Когда мы говорим о конкретном человеке или группах, общностях людей, мы привычно и естественно употребляем слово "человек". В большинстве случаев (более осознанно или менее осознанно) мы связываем это слово с каким-либо знанием общих свойств всех человеческих существ, их отличия от других объектов природы, от животных и т. д. Когда слово выступает в единстве с таким (более полным или менее полным, более расчлененным или менее расчлененным) знанием, оно как раз и фигурирует как понятие. Понятия - такие воплощенные в словах продукты социально-исторического процесса познания, которые выделяют и фиксируют общие существенные свойства, отношения предметов и явлений, а благодаря этому одновременно суммируют важнейшие знания о способах действия с данными группами предметов и явлений. Без понятий человеческое познание было бы невозможно. Если бы в ходе длительного исторического процесса человеческого познания не выработались и не закрепились такие обобщенные формы мысли, то каждый человек - в каждом поколении - вынужден был бы вновь и вновь описывать, сопоставлять и выражать отдельным словом каждую конкретную вещь, факт, явление. Пользуясь словами-понятиями, мы в сокращенной форме аккумулируем и используем итоги многовекового практического опыта человечества.

До сих пор мы говорили преимущественно о таких понятиях, которые фиксируют общие свойства материальных объектов. "Красное" - это понятие, отражающее общее свойство некоторых чувственно-наблюдаемых вещей и их отличие от других, иначе окрашенных материальных предметов. Когда же мы, далее, фиксируем не только различие красных, зеленых, желтых и т.п. предметов, но и их тождество, сходство, то на первый план выступает их объективное свойство быть так или иначе окрашенными, то есть свойство цвета. Формируется (наряду с понятиями "красного", "зеленого") также понятие "цвета", имеющее еще более общий характер, отражающее еще более общую связь. Для его образования, очевидно, надо уже так или иначе понимать связь и различие между конкретными красными предметами и красным вообще, то есть различие и связь между отдельным и общим. Понятие "цвета" учитывает не только общие свойства всех окрашенных вещей, но устанавливает отношения между ними и между словами-понятиями, фиксирующими отношения разных цветов: "красного", "зеленого", "желтого" и т.п. Такого рода слова-понятия фиксируют общие отношения вещей и явлений, но сами они уже являются не конкретными материальными, а идеальными, обобщенными объектами познания; при этом "уровень" или степень отвлечения от конкретности материальных предметов и их чувственно наблюдаемых свойств могут быть различными.

И все же применительно к тем понятиям, которые возникают и используются именно в непосредственном процессе материально-практической деятельности, необходимо вновь подчеркнуть их связь с чувственным познанием, наблюдением, чувственно-образным отражением действительности. Образные формы отражения свойств предметного мира сами уже заключают в себе первые этапы и формы обобщения. Например, если мы имеем в сознании образ собаки, то этот последний уже является довольно сложным результатом чувственного опыта - в нем так или иначе синтезированы черты разных собак, которых мы могли наблюдать. Образную форму всегда имеют и наши более общие, отвлеченные и целостные представления (о родине, о том или ином городе, стране и т.д.). При помощи понятий процесс обобщения не только продолжается: связь понятия со всей совокупностью вполне определенных предметов данного класса становится более опосредованной. Понятия "собака", "дерево", "стул", в отличие от соответствующих образов, могут быть лишены черт конкретности. И все же понятием (а не простым словом, простой совокупностью звуков) оно является только благодаря тому, что с его помощью мы вновь и вновь осваиваем, используем, обозначаем (а значит, указываем для других людей) соответствующие объекты и их отношения. В понятии (то есть в слове, которое тесно связано с совокупностью знаний) уже обобщаются и фиксируются такие знания, которые позволяют нам практически действовать с предметами соответствующего класса. Понятия как бы дают правила, некоторую сокращенную схему чувственно-практического действия. В этом - специфическая особенность понятий, которые формируются в ходе чувственно-предметной деятельности.

Обратим особое внимание на те действия, которые имеют место в процессе образования понятий такого рода. Строго взаимосвязанные действия отвлечения, сравнения и сопоставления, выделения того общего свойства, которое присуще необозримому множеству предметов и целым классам предметов, в философии именуются абстрагированием, а результаты познания, получаемые в итоге, называются абстракциями. При абстрагировании человек исходит из объективных, действительных свойств объектов и явлений и из их реальных отношений друг к другу; фиксируется их действительное, независимо от сознания существующее единство. Но при этом деятельность отвлечения и объединения, синтезирования свидетельствует о мощи и активности человеческого познания, о возникновении особого типа деятельности, особого типа познания, направленного на фиксирование отношений. Необходимо еще и еще раз подчеркнуть, что установление отношений, их познание, усовершенствование таких знаний и их использование в практике - дело весьма привычное и повседневное. Это процесс, который ежедневно и ежечасно осуществляют люди в своей жизни и который приводит к очень важным не только материальным, но и идеальным результатам. Мы воздействуем при помощи одних предметов на другие, потому что уже знаем или можем предположить, а затем точно узнать, в каком отношении они находятся друг с другом.

Древний человек был окружен в принципе теми же материалами природы, что и современный человек. Ему, например, попадались куски железа. Но человек не сразу понял, что из того материала, который содержится в этих кусках, можно сделать топор. Лишь после многих разрозненных, часто случайных действий люди обнаружили, что этот материал - железо - в силу особых свойств пригоден для обработки других предметов. Таким образом, изготовление орудий означает установление и осознание прочных отношений между используемыми для орудия материалами и некоторыми другими объектами материального мира. Человек использует данные материалы для постройки дома потому, что он уже знает отношение между необходимыми для постройки материалами и результатом - построенным домом.

Обнаружить, раскрыть эти отношения человеку помогает практический процесс активного использования одних предметов для воздействия на другие. Одновременно это процесс повторения, воспроизведения определенных действий, выявления некоторых прочных, устойчивых, повторяющихся отношений. Такие отношения определяются как существенные или закономерные объективные отношения и связи.

В процессе исторического развития деятельность по образованию и использованию понятий, первоначально включенная в непосредственную практическую деятельность и существовавшая только в этом виде, приобретает более сложные формы, а затем выделяется - очень медленно и постепенно - в самостоятельную деятельность.

Возьмем, к примеру, процесс познания количественных отношений. Сегодня он достиг очень важных научных и практических результатов: математизация знания есть одна из главных объективных тенденций развития наук в эпоху научно-технической революции. Вместе с тем многие понятия и представления о количественных отношениях приобрели такую абстрактность и отвлеченность, что иногда истолковываются как совершенно "свободные" и "произвольные" творения человеческого ума. Но нельзя забывать, что познание количественных отношений с давних пор было вплетено в практическую предметную деятельность человека и до сих пор продолжает развиваться также и в этой форме.

В ходе этого процесса люди с давних пор сначала научились сопоставлять, измерять определенные материальные объекты, потом уловили общность между своими действиями, направленными на измерение и пересчет различных объектов, и, подвергнув анализу эти действия, установили количественные отношения между самими материальными объектами. В их сознании сформировались знания о количественных отношениях, которые приобрели обобщенную форму, знаковое выражение и стали важнейшим фактором дальнейшей практической деятельности. Лишь впоследствии выделились особые группы людей, которые стали носителями знания о количественных отношениях и накопили специальные навыки работы с числами. Эти люди сначала занимались измерением земельных участков, подсчетом предметов и вещей, предназначенных для распределения между членами общины или для торговли и обмена; от этой деятельности лишь на сравнительно позднем этапе развития обособился тип деятельности, непосредственным и основным объектом которой стали сами числовые и геометрические отношения, рассматриваемые и изучаемые уже отдельно от исчисляемых и измеряемых предметов. Так возникла математика, древнейшая из наук. И сегодня деятельность по образованию и использованию понятий о количественных отношениях продолжает существовать в двух формах.

Во-первых, познавая объективные количественные характеристики материальных тел, предметов, процессов развития природы и общества, человек и сегодня привычно употребляет такие слова, как "меньше", "больше", "равны" и т.д. Человек повседневно пользуется числами. Именно в результате миллионы раз повторявшегося взаимодействия с различными материальными объектами человек выделил, познал количественные их характеристики и соотношения, обозначил их особыми языковыми знаками (знаки чисел 1, 3, 5..., операций "больше", "меньше", "равны" и т.д.). И сегодня он употребляет, использует на практике и уточняет "количественные" понятия.

Что же касается математики, то она уже имеет дело с различными результатами человеческого познавательного процесса, то есть со знаниями. Поскольку она использует знания, представления о количественных отношениях в процессе последующего, более глубокого осознания этих отношений, поскольку она выясняет, как соотносятся друг с другом сами числа, - происходит превращение "количественных понятий", то есть обобщенных знаний об отношениях объектов, в особые объекты познания. Создав математику, человек может работать непосредственно с числами как с объектами, на которые направлено его познание; он может - в результате работы с числами - получать новые формулы, выявлять определенные математические закономерности, то есть приобретать новые знания.

В пределах же гносеологии необходимо, во-первых, подчеркнуть значение и специфику процесса образования и функционирования понятий и, во-вторых, учитывать, что в ходе развития истории постепенно складывается особая деятельность, цель которой - формирование, изменение знаний, то есть формирование и изменение понятий, идей, теоретических концепций. Следовательно, в процессе общественного разделения труда возникает особый тип деятельности, который в конечном счете связан с задачей практического использования, изменения мира природы и общества, но который своей главной и непосредственной целью имеет производство теоретического знания (а также хранение, накопление, передачу, распространение знаний, обучение знанию). Это и есть специальная деятельность по созданию общих понятий, идей, принципов, которая в масштабах общества так или иначе организована в особый процесс.

Общая характеристика понятий

языковыми выражениями (терминами), а понятиями. Термин – выражение со строго фиксированным значением, входящее в состав предложения, но само предложением не являющееся.

Тами объема понятия αА(α).

рическое и арифметическое. Чтобы избежать неясности, сформулируем понятие о кубе: «правильный многогранник с шестью гранями (гексаэдр)». Универсум (род) этого… – множество всех многогранников. Содержание (видовое отличие) – сложный признак

Обобщение и ограничение понятий

обобщение и ограничение. Они основаны на отношении типа «родвид». Из двух непустых понятий одно считается родовым, а другое видовым, если второе… Например, из двух понятий αА(α)«европейский город» и αВ(α)«европейская сто-

А⊆ В≡ А(α)⊃ В(α).

1) «студент, сдавший все экзамены» и 2) «студент, сдавший хотя бы один экзамен». Объем первого понятия включается в объем

Виды понятий.

1) единичные и общие, 2) собирательные и несобирательные, 3) конкретные и абстрактные, 4) положительные и отрицательные, 5) безотносительные и… 1. Понятия делятся на единичные и общие в зависимости от того, мыслится в них… Общие понятия могут быть регистрирующими и нерегистрирующими.

А) Виды понятий по объему.

более важными основаниями для деления понятий являются: (1) тип их объема, (2) тип элементов, входящих в их объемы, (3) тип признаков, на основании которых… ся обобщение.

В) Виды понятий по типу элементов объема.

а) конкретные и абстрактные Конкретным считается понятие, элементами объема которого являются объекты или множества объектов (например, «человек, умеющий играть на скрипке»).

С) Виды понятий по содержанию.

а) положительные и отрицательные Положительным считается понятие, в котором предметы обобщаются на основа- нии признака, которым они обладают (например, «книга, взятая в библиотеке»).

Отношения между понятиями по объему.

Например, множество стульев изобразим следующим образом: Отдельный элемент будем обозначать точкой в круге, единичное множество - кругом.

Равнообъемность (равнозначность) - отношение между понятиями, которые, отличаясь содержанием, имеют одинаковый объем, то есть выделяют один и тот же класс предметов. Равнообъемными могут быть как общие понятия (например, «равноугольный ромб» (А) и «равносторонний прямоугольный четырехугольник» (В)) (рис.4), так и понятия единичные (например, «автор романа «Война и мир» и «автор романа «Анна Каренина»). Если в объемах сравнимых понятий нет ни одного общего элемента, то их следует считать несовместимыми.Имеются два вида несовместимости: отношение противоречияиотношение соподчинения.

1. 
   ^ Подчинение или включение объемов. В этом отношении находятся понятия, когда объем одного из них включен полностью в объем другого. Пусть В – «человек», а А – «живое существо».

Подчинение имеет место в том случае, если объем одного из понятий полностью входит в объем другого, составляя его часть. В отношении подчинения могут находиться общие понятия (например, «рыба» и «форель»). Этот случай принято называть родо-видовым отношением (рис.2), имея в виду то, что класс, выделенный более широким общим понятием А, является родом, к которому как вид принадлежит класс, выделенный понятием В, меньшим по объему (рыбы – род, одним из видов которого является форель). Кроме родовых и видовых общих понятий, в отношении подчинения могут находиться также общее понятие с единичным, например, «астроном» и «Кеплер».

 

1. 
   Исключение объемов - случай, в котором нет ни одного предмета, который находился бы в обоих объемах.

1. 
   Пересечение объемов, или частичное совпадение объемов. Например, в отношении «студент» и «отличник». Зона пересечения - это множество тех элементов, которые одновременно принадлежат множествам А и В.

Пересечение имеет место в том случае, когда объем одного из понятий частично входит, а частично не входит в объем другого понятия. Пересекаться могут только общие понятия, например, «женщина» и «инженер», «лошадь» и «домашнее животное», «белый предмет» и «рояль» и др. Во всех этих парах понятия совместимы частично: часть женщин является инженерами, но часть женщин имеют другую профессию, часть инженеров - женщины, но есть и инженеры - мужчины и т.д.

 

1. 
   Противоречие - отношение между понятиями, которые будучи несовместимыми исчерпывают суммой своих объемов объем более общего, родового по отношению к ним понятия. В отношении противоречия будут находиться два понятия, в одном из которых отрицаются признаки предмета, зафиксированные в другом понятии то есть: (В = не-А).

Например: «здоровый человек» и «нездоровый человек», «инженер» и «человек, инженером не являющийся» и др. Поскольку, согласно закону исключенного третьего, между А и не-А не существует промежуточного звена, положительные и соответствующие им отрицательные понятия всегда исчерпывают объем понятия, которому они подчинены (все люди либо инженеры, либо не-инженеры, «третьего не дано»).

6. Соподчинение имеет место тогда, когда два (или более) несовместимых понятий, не имея общих элементов в объемах, не исчерпывают объем родового для них понятия, которому они подчинены. Соподчиненными являются, например, понятия «телевизор» (В) и «экскаватор» (С), поскольку будучи несовместимыми между собой и подчиненные родовому понятию "техническое устройство" (А), они

Особым отношением является отношение соподчинения, когда объемы двух понятий, исключающие друг друга, входят в объем третьего понятия. Например, понятия «автобус» и «трамвай» попадают в одну категорию – «городской транспорт».

Иногда соподчиненные понятия внешне выглядят как противоречивые. Это касается тех случаев, когда понятия выделяют классы предметов, находящихся как бы на противоположных краях объема родового понятия, которому они подчинены. Возьмем, например, понятия «отличник» и «двоечник». На первый взгляд, они противоречивы, поскольку отрицают друг друга. Однако анализ их отношения с родовым для них понятием «учащийся» показывает, что отношения противоречия между ними нет. Последнее имело бы место, если бы объем понятия «учащийся» равнялся сумме объемов наших двух понятий. Но в действительности среди учащихся есть еще троечники, хорошисты. Поэтому рассмотренный случай является разновидностью отношения соподчинения, а не противоречия⁴.

___________________________________________________________

Между понятиями существуют объективные, независящие от человека отношения.

Прежде всего, это отношения сравнимости и несравнимости.

Два понятия αА(α)и αВ(α)являются сравнимыми,если и только если их уни-

версумы совпадают. Например, понятия о преступнике и о жертве преступления яв-

ляются сравнимыми. Оба они относятся к одной и той же предметной области – уни-

версуму людей.

Два понятия αА(α)и αВ(α)являются несравнимыми,если они относятся к различ-

ным универсумам. Например, понятие о четном числе и понятие о европейской столице

являются несравнимыми, поскольку первое из них имеет своим родом универсум чисел, а

второе – универсум городов.

Среди всевозможных пар сравнимых понятий можно выделить три фундаменталь-

ных отношения в том смысле, что с их помощью легко задать все остальные отношения. В

число фундаментальных входят отношения совместимости, включения и исчерпывания.

Фундаментальные отношения:

1) Понятия αА(α)и αВ(α)находятся в отношении совместимости, если и только если

пересечение их объемов Аи Внепусто, то есть

А∩ В≠ ∅.

Это означает, что в универсуме имеется по крайней мере один элемент, обладающий

как признаком А(α),так и признаком В(α) (например, А– студент, В– спортсмен).

2) Понятие αВ(α) находится к понятию αА(α) в отношении включения, если и только если

при вычитании объема αА(α) из объема αВ(α) получается пустое множество, то есть

ВA =∅.

Это означает, что всякий элемент универсума, обладающий признаком В(α),обладает

также признаком А(α)(например, А– учащийся, В– студент).

3) Понятия αА(α) и αВ(α) находятся в отношении исчерпывания, если и только если

объединение их объемов А и В равно универсуму, то есть

А∪ В = U.

Это означает, что каждый элемент универсума обладает признаком А(α)или призна-

ком В(α)(например, А– сын5956 0 , В– дочь; каждый человек является чьим-то сыном или

дочерью).

Вспомогательные отношения выводятся из фундаментальных. Наиболее важны-

ми из них являются: равнообъемность, подчинение, соподчинение, перекрещивание, противоре-

чие, дополнительность. Рассмотрим их на кругах Эйлера1.

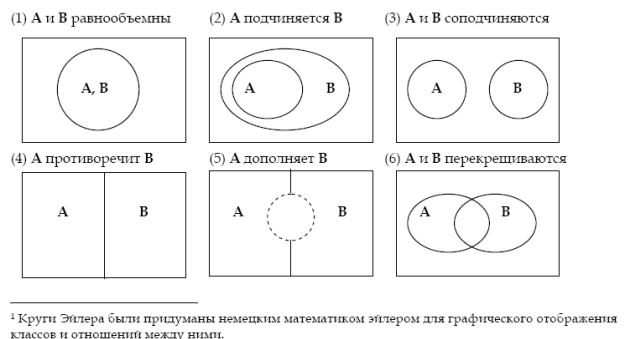
Примеры:

1) Равнообъемность: «параллелограмм, имеющий равные углы и стороны» (А)и «параллело-

грамм, имеющий равные диагонали» (В).

2) Подчинение: «город, расположенный в Европе» (А)и «город, расположенный на материке Ев-

разия» (В).

3) Соподчинение: «остроугольный треугольник» (А)и «тупоугольный треугольник» (В).

4) Противоречие: «животное, умеющее плавать» (А)и «животное, не умеющее плавать» (В).

5) Дополнительность: «территория, находящаяся севернее Южного Тропика» (А)и «терри-

тория, находящаяся южнее Экватора» (В).

6) Перекрещивание: «человек, изучающий логику» (А)и «человек, изучающий немецкий язык» (В).

Все перечисленные объемные отношения между понятиями можно обобщить при

помощи следующей таблицы:

Примечание: символ * означает: «при условии, что А и В являются непустыми и неуниверсаль-

ными понятиями» (если это условие не выполнено, то в ячейках с * могут стоять другие отметки, а по-

нятия могут находиться друг к другу в нескольких логических отношениях одновременно).

Обратите внимание, что структура логических отношений между понятиями

очень похожа на структуру отношений между суждениями.

Упражнение 6.Используя приведенные выше определения, скажите, в каких от-

ношениях будут находиться объемы понятий А и В, если их содержания находятся в от-

ношении:

а) контрарности;

б) субконтрарности;

в) независимости;

г) эквивалентности.

Когда сравнивается большое число понятий, круговые схемы могут служить хо-

рошим средством для наглядного отображения отношений между этими понятиями.

Предположим, нам надо сравнить понятия о следующих предметах: (1) летательный ап-

парат тяжелее воздуха, (2) летательный аппарат легче воздуха, (3) самолет, (4) пассажирский

самолет, (5) дирижабль, (6) воздушный шар, (7) пилот дирижабля

Построим единую круговую диаграмму. Универсум – общий род большинства

сравниваемых понятий – летательные аппараты.

Операции ограничения, обобщения, деления. Виды и правила деления.

Операции с понятиям

В практике общения между людьми возникает необходимость в уточнении отдельных высказываний. Например, «Студенты изучают логику». Но все ли студенты? Нет, не все, а только студенты пер­вого курса юридического факультета.

В процессе мышления совершаются четыре основные операции: обобщение, ограничение, определение и деление понятий.

Обобщение понятия- это логическая операция, которая состоит в переходе от понятия с меньшим объемом (большим содержанием) к понятию с большим объемом (но меньшим содержанием). Обобщение понятий - это переход от вида к роду. Например, обобщая понятия «министерство юстиции России» - к понятию «министерство юстиции». Обобщение понятий происходит путем отбрасывания из содержания исходного понятия какого-либо индивидуального, видового, признака. Пределом обобщения являются категории - понятия с предельно широким объемом, например: «материя», «сознание», «движение», «свойство» и т. д.

Ограничение понятия- логическая операция, которая состоит в переходе от понятия с большим объемом (и меньшим содержанием) к понятию с меньшим объемом (но с большим содержанием). В процессе ограничения происходит переход от родовых понятий к видовым. Достигается это путем добавления к содержанию исходного понятия какого-либо нового признака. Например, понятие «юрист» можно ограничить, добавив признаки о специфике профессиональной деятельности юриста, например, «быть следователем» - получится понятие «следователь»; добавив признак «быть следователем прокуратуры», можно получить понятие «следователь прокуратуры» и т. д.

Понятие «деяние» можно ограничить следующим образом: «преступное деяние» (т. е. «преступление») → «должностное преступление» → «получение взятки» -» «получение взятки заведующим базой Петровым». Пределом ограничения являются единичные понятия.

Операции обобщения и ограничения понятий часто применяются в процессе мышления: переходя от понятия с одним объемом к понятию с более узким или, наоборот, более широким объемом, мы уточняем предмет нашего мышления, делаем мышление более определенным, последовательным, точным.

Определение понятий - это такая логическая операция, с помощью которой раскрывается (уточняется) содержание понятия. Определить понятие о предмете - значит указать существенные признаки этого предмета. Например: «Кража - тайное хищение чужого имущества»; «Человек - живое существо, способное производить орудия труда». Понятие, содержание которого уточняется (например, «кража»), - это определяемое понятие, или дефиниендум (сокращенно Dfd). Понятие, с помощью которого происходит уточнение содержания исходного понятия («хищение», «чужое имущество», «тайное»), - это определяющее понятие, или дефиниенс (сокращенно Dfri).

Рассмотрим виды определений:

1. По способу выявления содержания понятий выделяются явные и неявные определения. Наиболее часто применяемым явным определением понятий является определение через род и видовое отличие, в котором предметы, о которых говорится в определяемом понятии, сначала соотносятся с предметами ближайшего рода, а затем указывается тот видообразующий признак, при помощи которого определяемый предмет выделяется из множества предметов данного рода. Так, определяя понятие «кража», вначале указывается его родовой признак - «хищение чужой собственности», затем с помощью видового признака - «тайное» - выделяют данный вид преступле­ний среди других преступлений против собственности.

Неявные определения - такие, в которых содержание понятий раскрывается косвенным путем. К ним принадлежат:

• контекстуальные определения - когда содержание понятий раскрывается через контекст - отрывок письменной или устной речи, в которой используются данные понятия; например, «на данный вопрос я прошу вас ответить категорически - да или нет»;

• остенсивные - определения, раскрывающие существенные признаки предметов путем их указания, показа: «это ручка», «это книга, по которой будете изучать логику»;

• определения через отношение - понятие «материя» определяется через отношение к «сознанию», «свобода» через отношение к «необходимости», «причина» - через отношение к «действию», «необходимость» - через отношение к «случайности» и т.д.

К приемам, заменяющим определения, относятся описание, характеристика, сравнение.

2. В зависимости от того, что именно определяется (предметы или слова), различают реальные и номинальные определения. Реальным является определение, раскрывающее существенные признаки предметов. Например, улика - доказательство виновности обвиняемого в совершении преступления. Реальные определения строятся по схеме: «Предметы вида А есть предметы рода В, имеющие признаки с», сокращенно А = Вс.

Номинальным является определение, посредством которого вводится новый термин (имя), объясняется значение термина, его происхождение и т. д. Например, термином «улика» обозначается доказательство виновности обвиняемого в совершении преступления. Термин «юридический» обозначает все, относящееся к правоведению, праву. Номинальное определение отвечает на вопрос, что обозначает то или иное выражение, и строится по схеме: «Выражение "А" обозначает предметы В, имеющие признаки с». Например: «Слово "кинология" обозначает науку о собаках, их породах, разведении и уходе за ними» или «Покровительство, оказываемое влиятельным лицом кому-либо в устройстве его дел, называется протекцией».

В процессе мышления следует соблюдать следующие четыре основные правила определения.

Правила определения (касаются структуры, формы определения).

1. Определение должно быть соразмерным, т. е. объем определяемого понятия должен быть равен объему определяющего понятия. Например, «грабеж - открытое хищение чужого имущества», «рецидивист-лицо, совершившее преступление после осуждения за ранее совершенные преступления». Схематично: А - Вс, или Dfd = Dfn.

При несоблюдении данного правила возможны две ошибки: а) слишком широкое определение - объем определяющего понятия шире объема определяемого понятия, например, «рецидивист - лицо, совершившее преступление»; б) слишком узкое определение -объем определяющего понятия уже объема определяемого, например, «рецидивист - совершивший вторично убийство».

2. Определение не должно заключать в себе круга. Круг в определении возникает тогда, когда понятие А определяется через понятие В, а В в свою очередь определяется при помощи понятия А. Разновидностью круга в определении является тавтология - ошибочное определение, в котором определяющее понятие повторяет определяемое: «то же - через то же». Например: «идеалист – человек идеалистических убеждений», «свидетель - лицо, дающее свидетельские показания», «лекарство - то, что лечит».

3.Определение должно быть ясным, т.е. в определяющем понятии должны указываться известные признаки, не нуждающиеся в определении и не содержащие двусмысленности. Если же понятие определяется через другое понятие, которое само нуждается в определении, то это ведет к ошибке, называемой определением неизвестного через неизвестное. Это правило предостерегает от подмены операции определения понятий сравнениями, метафорами, которые не раскрывают существенных признаков предмета. Например, не являются определениями: «государство - политическое проявление мирового духа» (Гегель); «смех есть солнечный свет в жизни»; «повторение - мать учения».

4.Определение по возможности не должно содержать в определяющем понятии отрицательных признаков. Определяющее понятие должно указывать признак, принадлежащий предмету, а не отсутствующий у него. Но это требование не является строгим логическим правилом, обязательным при определении любого понятия. Отрицательные определения широко применяются в математике и в других науках. В некоторых случаях определение понятий (как правило, содержащих приставку «без», «не», «а») возможно только через отрицание. Например: «бесхозное имущество - имущество, не имеющее собственника или собственник которого не известен», «безбожник - это человек, не признающий существования Бога».

Определение понятий играет важную роль в теоретической и практической деятельности. Раскрывая главное в предмете, определение позволяет выделить данный предмет, отличить его от других предметов, предостерегает от смешения понятий, от путаницы в рассуждениях. В любой науке всем основным понятиям даются точные определения; большое значение имеет определение понятий в правовых науках. По существу, любой Уголовный кодекс состоит из понятий и их определений (изложенных в соответствующих статьях). Ошибочное толкование понятий (например, понятий «умысел», «соучастие», «вина», «неосторожность» и т. д. в уголовном праве) может привести к неправильному пониманию отражаемых в них явлений, а следовательно, к ошибкам суда и следствия.

Итак, определение раскрывает содержание понятий. Но понятие, как мы уже знаем, состоит из содержания и объема. К объему понятий применима операция деления понятий.

Деление понятий - это логическая операция, раскрывающая объем понятия. В процессе деления объем понятия распределяется на группы. Элементами деления являются: делимое - понятие, объем которого требуется раскрыть; члены деления - соподчиненные виды, на которые делится понятие; основание деления - признак, по которому производится деление. Например, учеников в школе можно разделить на классы, в классах - на группы по различным признакам: спортсмены и неспортсмены; изучающие английский язык, немецкий и французский языки и т. п. Сделки (соглашения) можно разделить на многосторонние, двусторонние и односторонние.

Необходимо отличать логическое деление от мысленного расчленения целого предмета на части. Если мы скажем, что человек состоит из головы, ног, рук и т.д., то это не будет логическим делением понятия «человек».

Различают деление по видообразующему признаку и дихотомическое деление. По видообразующему признаку деление может производиться - по какому-то основанию - на несколько разных видов; в дихотомическом деление производится на два вида.

Дихотомическое (от греч. слов - dicha и time, означающих «сечение на две части») - деление объема делимого понятия на два противоречивых понятия. Например, А - граждане России, В - совершеннолетние, С - несовершеннолетние. Всех учеников можно разделить на курящих и некурящих; спортсменов и неспортсменов; любящих классическую музыку и не любящих ее и т. п.

Видом операции деления является классификация. Классификация - распределение предметов по группам (классам), при котором каждый класс имеет свое постоянное, определенное место. Вспомним классификацию химических элементов в периодической таблице Менделеева или распределение книг в библиотеке по предметному или алфавитному каталогу. Например, в Особенной части Уголовного кодекса все составы преступлений делятся сначала по различию в объекте посягательства: преступления против личности; преступления в сфере экономики; преступления против общественной безопасности и общественного порядка; преступления против государственной власти; преступления против воинской службы и преступления против мира и безопасности человечества. Затем каждый из этих видов делится в свою очередь на подвиды. Таким образом, все виды преступлений распределяются по группам, причем каждый вид (группа) занимает строго определенное место, закрепленное соответствующей статьей Уголовного кодекса.

Чтобы правильно производить операцию деления, необходимо знать правила деления понятий.

1. Деление должно быть соразмерным, т. е. объем делимого понятия должен быть равен сумме объемов всех членов деления.

Возможные ошибки при нарушении этого правила:

а) неполное деление (когда перечислены не все члены деления). Например, «допросы делятся на допросы потерпевшего и допросы обвиняемого» (не указаны допросы свидетелей, подозреваемого);

б) деление с лишними членами (когда среди членов деления встречается понятие, объем которого не входит в объем делимого понятия). Например, если при делении понятия «наказание» мы укажем «предупреждение», которое не входит в перечень мер наказания в уголовном законодательстве, а является видом административного взыскания, то совершим ошибку (укажем лишний член).

2. Деление должно производиться только по одному основанию. Это значит, что в процессе деления выбранный признак должен оставаться тем же и не подменяться другим. Ошибки при несоблюдении этого правила называются: «не по одному основанию» или «сбивчивое деление». Например, деление преступлений на умышленные, неосторожные и воинские - сбивчивое, произведено не по одному основанию.

3. Члены деления должны исключать друг друга. Это правило вытекает из предыдущего. Например, при делении студентов на заочников, первокурсников и спортсменов подклассы предметов не исключают друг друга: студенты-заочники могут быть первокурсниками и спортсменами; первокурсники могут быть заочниками и спортсменами и т. д. Таким образом, члены деления - перекрещивающиеся понятия. При делении объема понятия «преступление» на понятия «умышленное преступление», «неосторожное преступление» и «воинское преступление» нарушается и второе, и третье правила. При смешении оснований деления члены деления (видовые понятия) будут частично совпадать.

4. Деление должно быть непрерывным. Это значит, что в процессе-деления родового понятия нужно переходить к ближайшим видам, не пропуская их. Например, понятие «преступление» можно разделить на понятия «государственное преступление», «должностное преступление», «воинское преступление» и т. д. В свою очередь каждое из этих видов можно разделить на подвиды. Так, понятие «воинское преступление» можно разделить на «неисполнение приказа», «угроза начальнику», «самовольная отлучка» и т. д. Ошибка, которая возникает при нарушении этого правила, называется «скачком в делении».

Операция деления (и классификация) помогает глубже познавать класс предметов в целом и каждый предмет в отдельности. Эта операция имеет большое значение в работе юриста. Например, она лежит в основе таких действий, как: планирование расследования преступлений, классификация следственных версий и т. д.; в криминалистике классифицируются лица, совершившие преступления, предметы (орудия преступления, следы, документы и т. п.). Знание правил деления и классификации необходимо при изучении больших групп явлений и для их упорядочивания. Операция деления позволяет глубже изучить свойства предметов, найти какие-то закономерности во взаимосвязях предметов и их свойствах, облегчает поиск необходимых предметов (как, например, ту или иную книгу в библиотеке, ученика по номеру класса или группы, в которой он учится, и т. п.).

Итак, понятие- мысль, отражающая предметы со стороны их существенных признаков. Каждая отрасль знаний или отдельный ее фрагмент имеют свою терминологию, выражающую систему понятий, в которых зафиксирована накопленная информация о закономерных и наиболее существенных связях и отношениях между соответствующими объектами. Овладение конкретной областью знаний предполагает прежде всего уяснение системы употребляемых в ней понятий.

Обобщение и ограничение понятий

обобщение и ограничение. Они основаны на отношении типа «родвид». Из двух непустых понятий одно считается родовым, а другое видовым, если второе… Например, из двух понятий αА(α)«европейский город» и αВ(α)«европейская сто-

А⊆ В≡ А(α)⊃ В(α).

1) «студент, сдавший все экзамены» и 2) «студент, сдавший хотя бы один экзамен». Объем первого понятия включается в объем

Деление и классификация

Еще одной важной операцией является деление понятий.

Деление некоторого непустого понятия αВ(α) –это переход от данного понятия к

некоторой системе непустых понятий S = {αА1(α),αА2(α), …,αАn(α)},каждое из которых

является видовым по отношению к исходному.В состав деления входят:

1) Делимое понятие – родовое понятие αВ(α), объем которого разбивается на классы.

2) Члены деления – видовые понятия αА1(α),αА2(α), …,αАn(α), полученные в резуль-

тате такого разбиения.

3) Основание деления –характеристика предметов, входящих в объем делимого по-

нятия, модификация которой и порождает систему членов деления S.

В зависимости от выбранного основания деления, различают следующие виды де-

ления: дихотомическое и по видоизменению основания.

В случае дихотомического деления родового понятия αВ(α) основанием деления

является признак, присущий лишь части предметов, входящих в объем αВ(α). Деление

осуществляется по наличию или отсутствию этого признака у предметов делимого поня-

тия. Например:

Упражнение 9.Осуществите деление следующей группы имен десятью различ-

ными способами: (1) Алиса, (2) Навуходоносор, (3) Додон, (4) Александр, (5), Марлен, (6) Герда,

(7) Екатерина, (8) Мафусаил, (9) Октябрина, (10) Николай, (11) Евдудндокта, (12) Мария.

Правила деления

1) Правило полноты: объединение объемов членов деления должно совпадать с объе-

мом делимого понятия.

А1∪А2∪…∪Аn = В.

При нарушении данного правила возникает ошибка под названием «неполное де-

ление». Пример: люди делятся на брюнетов и блондинов (пропущены классы шатенов, ры-

жих и т.д.). Простейший способ избежать этой ошибки – всегда включать в систему деле-

ния категорию «и прочие».

2) Правило исключения (четкости): все члены деления должны быть попарно несовмес-

тимы друг с другом:

для любых i, j ≤ n Аi∩Аj =∅.

При нарушении данного правила возникает ошибка «перекрещивающееся деле-

ние». Пример: писатели делятся на поэтов и прозаиков (писатель может быть одновременно

и тем, и другим).

Заметим, что в науке часто используется прием, сходный с делением, – типологи-

зация. Под типологизацией понимают расчленение системы объектов на группы, обла-

дающие сходным структурным строением или функцией (типы). В отличие от логиче-

ского деления, здесь предполагается, что один и тот же объект может относиться сразу к

нескольким типам, поэтому данное правило к типологиям не применимо.

3) Правило единства основания: деление должно осуществляться по одному основа-

нию. При несоблюдении данного правила возникает ошибка «сбивчивое деление».

Если деление сбивчивое, оно довольно часто оказывается также неполным или пере-

крещивающимся.

Колоритный примерсбивчивого деления приводит аргентинский писатель

Х.Л. Борхес. Оно представляет собой отрывок из «некой китайской энциклопедии», где

дается классификация животных и говорится, что они «подразделяются на: а) принадлежащих императору, б) бальзамированных, в) прирученных, г) молочных поросят, д) сирен, е) сказочных, ж) бродячих собак, з) заключенных в настоящую классификацию, и) буйствующих, как в бе зумии, к) неисчислимых, л) нарисованных очень тонкой кисточкой из верблюжьей шерсти, м) и

прочих, н) только что разбивших кувшин, о) издалека кажущихся мухами».

Итак, правильное деление – это такое деление, которое по одному и тому же осно-

ванию разбивает объем исходного понятия αВ(α)на непересекающиеся объемы видовых

понятий αАi(α),причем делает это так, что в сумме они исчерпывают весь объем родово-

го понятия: вне возникшей видовой системы не должно оказаться ни одного элемента из

объема αВ(α).

Операцию деления иногда путают с операцией мысленного разбиения предмета

на части. Такая операция еще называется мереологическим делением (мереология – наука

о соотношениях части и целого). В этом случае вместо перечисления видовых понятий

перечисляются понятия о частях предмета.

Пример:

«Скелет человека делится на скелет туловища, скелет головы и скелеты конечностей».

Ошибка обнаруживается следующим образом. Для каждого видового понятия

αА(α)должно быть истинным высказывание «Всякий Аесть В», в то время как ни для од-

ного понятия о частях предмета такое высказывание истинным не будет.

Чтобы подчеркнуть отличие от мереологического деления, логическое деление

называют иногда таксономическим, поскольку в результате оно дает соподчиненные

группы объектов – таксоны.

Упражнение 10. Определите, какие ошибки допущены в следующих делениях:

а) «Государства делятся на республиканские, монархические и демократические»;

б) «Семьи делятся на бездетные и многодетные»;

в) «Студенты делятся на тех, кто изучает английский язык, и тех, кто изучает немецкий язык»;

г) «Год делится на весну, лето, осень и зиму»;

д) «Женщины бывают двух видов: ужас какие умные и прелесть какие глупенькие»;

е) «Людей можно делить по-разному! Это известно всем». – И сказал удивленный палач: «А я-то всю жизнь делю их только на головы и туловища!» (С.Е. Лец).

Классификация – результат последовательного деления некоторого понятия на его

виды, видов на подвиды и т.д. Классификации крайне важны в научных исследованиях,

когда требуется привести полученные знания в единую стройную систему.

Для построения классификации могут быть использованы оба вида деления. При-

чем каждый этап классификации может осуществляться по собственному основанию, от-

личному от оснований, использованных на других этапах деления.

Всякая классификация может быть представлена в виде дерева понятий. Дерево

понятий – это множество точек (вершин), соединенных линиями (ребрами). Каждая вер-

шина представляет собой некоторое понятие – таксон. Ребра показывают, на какие под-

виды разбиваются таксоны. Вершина К0 называется корнем дерева. Она представляет ис-

ходное делимое понятие. Таксоны группируются по ярусам. В каждом ярусе собраны так-

соны, полученные в результате одинакового числа применений операции деления к

исходному понятию. Те таксоны, которые далее уже не делятся в данной классификации

на подвиды, называются концевыми таксонами.

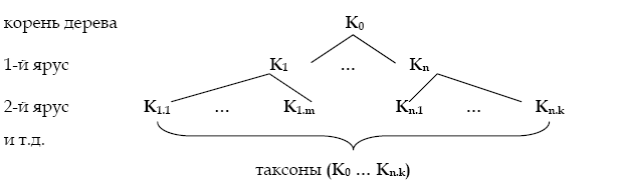
Предельной классификацией называется такая классификация, все концевые так-

соны которой представляют собой единичные понятия. Однако в зависимости от того,

для чего предназначена классификация, она может и не быть предельной.

В зависимости от характера оснований, выбранных для создания классификации,

классификации подразделяются на два вида: искусственные и естественные.

Искусственной считается классификация, в которой в качестве оснований деления

используются второстепенные, несущественные характеристики предметов.

Естественной считается классификация, в которой в качестве оснований деления

используются существенные характеристики предметов.

Существенными, как правило, называются те характеристики предмета, которые ис-

пользуются для теоретически научного описания этого предмета. Такие характеристики

являются наиболее фундаментальными по сравнению с другими характеристиками этого

предмета, составляют его «сущность». Их знание позволяет получить разнообразную до-

полнительную информацию о предмете, являющемся носителем этих характеристик.

Основная особенность естественных классификаций заключается в том, что зная

местоположение предмета в такой классификации, можно сразу же сказать о многих дру-

гих важных его свойствах (как, например, периодическая таблица Д.И. Менделеева).

Искусственные классификации тоже бывают очень важны. Они ничего не говорят

о других свойствах предмета, однако часто облегчают его поискпериодическая таблица Д.И. Менделеева).

Искусственные классификации тоже бывают очень важны. Они ничего не говорят

о других свойствах предмета, однако часто облегчают его поиск (как, например, алфавитный каталог книг в любой библиотеке).

Так как в основе всякой классификации лежит деление, то классификация считается правильной, если на каждом ее этапе деление было выполнено правильно. При этом

необязательно, чтобы в пределах одного яруса все деления производились по одному и

тому же основанию. Главное, чтобы требование единства основания не нарушалось в

рамках каждого отдельно взятого деления.

Упражнение 11.Постройте одну естественную и одну искусственную классификацию для следующих видов спорта. Каждая классификация должна состоять не менее

чем из трех ярусов.

(1) футбол, (2) хоккей, (3) теннис, (4) бобслей, (5) бейсбол, (6) водное поло, (7) борьба, (8)

волейбол, (9) лыжи, (10) плавание, (11) биатлон, (12) бокс, (13) баскетбол, (14) шахматы.

Определение. Виды и правила.

Определение и приемы, сходные с ним

пренебрегает требованием точности, однозначности. Это может привести к взаимному недопониманию и даже недоразумениям. Отсюда понятно, насколько важным… требование связывать с терминами языка строго определенный смысл.

Явные определения

Наиболее распространенный вид определений – явные определения. Определение

называется явным, если и только если оно задается лингвистической конструкцией вида:

А↔В.

Здесь Апредставляет собой определяемую часть (дефиниендум), В– определяю-

щую часть (дефиниенс), а символ «↔« выражает конвенцию использовать Ав значении В.

По содержанию дефиниенса, явные определения подразделяются на четыре типа:

1) квалифицирующие – определяют значение термина как предмет, обладающий неко-

торыми отличительными признаками. Например, «Нищий – это человек, живущий по-

даянием». Здесь указывается отличительный признак нищего – жить подаянием.

2) генетические – указывают на способ возникновения (порождения) предмета. В ка-

честве примера можно привести шуточное определение, принадлежащее извест-

ному математику Давиду Гильберту: «Каждый человек имеет некоторый определенный

горизонт. Когда он сужается и становится бесконечно малым, он превращается в точку.

Тогда человек говорит: «Это моя точка зрения». Здесь указывается механизм возник-

новения точки зрения – она получается путем сужения личного горизонта.

3) операциональные – указывают на операцию распознавания предмета. Например,

«Кислота – это жидкость, окрашивающая лакмусовую бумажку в красный цвет». Данное

определение позволяет всегда распознать кислоту с помощью стандартной опера-

ции с использованием лакмуса.

4) целевые – раскрывают предназначение предмета. Например, «Батут – это устрой-

ство для прыжков и подскоков». Здесь указывается, для чего предназначен батут и

тем самым разъясняется смысл соответствующего термина.

Заметим, что приведенный выше перечень представляет собой не строгое деление,

а типологию. Это означает, что каждое отдельно взятое определение может относиться

одновременно к нескольким типам. Например, следующее определение:

Документ есть такое письменное доказательство, которое выдано или заверено компе-

тентным органом в пределах его прав и обязанностей, в установленном законом порядке, содер-

жащее наличие всех необходимых реквизитов (дату выдачи, подпись должностного лица, указание

организации или органа, выдавшего документ, и т.д.).

Является одновременно генетическим (поскольку в нем указывается способ воз-

никновения документов) и квалифицирующим (поскольку в нем упоминаются особен-

ности оформления документов).

Особенностью всех явных определений является то, что дефиниендум и дефини-

енс могут в любом экстенсиональном1 контексте замещаться друг на друга. Для них дей-

ствует правило замены по дефиниции:

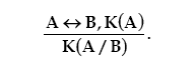
Это правило гласит, что если Аи Впо дефиниции означают одно и то же, все, что

может быть сказано относительно А, справедливо и относительно В. Другими словами, на

основании явного определения всегда можно перейти от контекста К(А)к контексту

К(А/В),где А/Весть замена Ана В.Правило замены по дефиниции позволяет использо-

вать явные определения в процессах дедуктивного вывода.

Упражнение 2.Определите термин «джентльмен» четырьмя различными спосо-

бами. Раскройте также смысл этого термина при помощи операций сравнения и описа-

ния. При возможности используйте и остенсивное определение.

 

Неявные определения

В науке и в юридической практике иногда используются определения, не имею-

щие вид равенства А↔В, то есть не относящиеся к явным определениям. Такого рода оп-

ределения называются неявными и задаются лингвистической конструкцией вида:

А есть то, что удовлетворяет пунктам] В1, В2, …, Вn.

фраза в квадратных скобках чаще всего подразумевается неявно. В зависимости от того, 1 Об экстенсиональных и интенсиональных контекстах что представляют собой сами пункты В1, В2, …, Вn, такие определения делятся на три ви-

Х + 0 = х.

Х + у’ = (х + у)’.

Первый пункт определения (базис рекурсии) утверждает, что значение функ-

ции х + уравно хв том случае, если у = 0. Второй пункт (рекурсия) говорит, что если мы

хотим вычислить значение х + у’, где у’– число, следующее за у, то надо вычислить для

этого у, чему равно х + у, и взять следующее за х + учисло.

Аксиоматические определения разъясняют значение некоторого термина путем

указания той совокупности аксиом, в которой он содержится.

Обычно мы идем противоположным путем: зная значение терминов, входящих в

высказывание, мы затем решаем вопрос о его истинности или ложности. Но поскольку

аксиомы уже заранее считаются истинными утверждениями, каждый входящий в них

термин косвенным образом получает определенный смысл и значение. Например, счита-

ется, что аксиомы Евклида неявно определяют термины «точка», «прямая», «плоскость», ааксиомы классической логики высказываний неявно определяют понятия отрицания,

импликации, конъюнкции, дизъюнкции и т.д.

Упражнение 3.Постройте несколько неявных определений, а именно:

а) индуктивное определение термина «предок»;

б) индуктивное определение термина «круглая годовщина»;

в) рекурсивное определение операции умножения;

г) рекурсивное определение операции возведения в квадрат.

Контекстуальные и неконтекстуальные определения

По составу дефиниендума определения делятся на контекстуальные и неконтекстуальные.

Неконтекстуальные определения используются чаще всего – они позволяют раскрыть смысл термина самого по себе, вне зависимости от какого-либо контекста. Структура таких определений проста:

А = df В.

Читается: «Аесть Впо дефиниции».

В контекстуальных определениях термин определяется не сам по себе, а в контексте какого-то предложения. Структура контекстуального определения имеет вид:

К(А)≡ df В.

если В». Определяемая и определяющая части здесь представляют собой не понятия, а суждения. Контекстуальные определения используются тогда, когда значение термина трудно объяснить вне контекста. Например, что…

Реальные и номинальные определения

стуальные и неконтекстуальные, их можно делить также на реальные и номинальные. При этом следует различать семантически и прагматически реальные и… определения.

Правила определения

принципиальные требования. Некоторые из этих требований носят всеобщий характер, а некоторые имеют силу лишь для дефиниций определенного вида. 1) Определение должно быть ясным. Это означает, что термины, из которых состоит

Понятие аргументации. Структура и виды аргументации.

(смотреть отдельный файл - 17-Вопрос-Понятие,основные виды аргументации)

Вопрос-Понятие,основные виды аргументации.doc

На ступени абстрактного мышления результаты процесса познания проверяют главным образом сопоставлением полученных результатов с другими, ранее… истинность суждений устанавливается логическим способом — через посредство… Такая опосредованная проверка суждений называется операцией обоснования, или аргументацией. Обосновать какое-либо…

Структура и субъекты аргументации

Обязательными участниками, или субъектами, аргументативного процесса являются: пропонент, оппонент и аудитория. 1. Пропонентом называют участника, выдвигающего и отстаивающего определенное… 2. Оппонентом называют участника, выражающего несогласие с позицией пропонента. Оппонент может непосредственно…

Структура аргументации

1. Тезис — это выдвинутое пропонентом суждение, которое он обосновывает в процессе аргументации. Тезис является главным структурным элементом… 2. Аргументы, или доводы, — это исходные теоретические или фактические… В качестве аргументов могут выступать различные по своему содержанию суждения: (1) теоретические или эмпирические…

Способы аргументации: обоснование и критика

Взаимосвязь позитивной и негативной информации в содержании убеждений предопределяет сложный, полемический характер самой процедуры аргументации,…

Обоснование тезиса

1. Прямым называют обоснование тезиса без обращения к конкурирующим с тезисом допущениям. Прямое обоснование может принимать форму (1) дедуктивных умозаключений, (2)… (1) Дедуктивное обоснование чаще всего выражается в подведении частного случая под общее правило.

Правила и ошибки по отношению к тезису.

Правила и ошибки в аргументации

Под логической ошибкой обычно имеют в виду непреднамеренное нарушение правил логики в процессе рассуждения по причине логической небрежности либо… 1. Правила и ошибки по отношению к тезису Тезис является центральным пунктом рассуждения, раскрытию и обоснованию которого подчинен весь процесс аргументации. …

Подмена тезиса.

(1) Полная подмена тезиса проявляется в том, что, выдвинув определенное положение, пропонент в итоге фактически обосновывает нечто другое, близкое… (2) Частичная подмена тезиса выражается в том, что в ход, выступления…  

Правила и ошибки по отношению к аргументам.

Логическая состоятельность и доказательное значение рассуждения во многом… Решение стратегической задачи аргументации определяется выполнением следующих требований, или правил в отношении…

Виды аргументации по форме. Правила и ошибки по отношению к форме аргументации.

Выделим основные черты дискуссии: 1. Субъектная структура внешне такая же, как и в споре. Но ее субъекты… 2. Тезисы сторон могут быть не только взаимоисключающими, но и взаимодополняющи­ми.

Правила и ошибки по отношению к демонстрации

Правила и ошибки по отношению к форме аргументации и критики

При нарушении этого правила возникает ошибка "не подтверждает". Применительно к доказательству она имеет название "не… Аргументируя или исследуя готовую аргументацию, важно знать, какова логическая… Со временем, если постоянно практиковаться в анализе рассуждений, логическая культура возрастет, карандаш будет…

Виды аргументов

- Теоретические или эмпирические обобщения; - Утверждения о фактах; - Аксиомы;

Аргументация может быть как прямой, так и косвенной.

Выделяется также полная и сокращенная аргументация. Полная аргументация содержит тезис и все доводы, которых требует используемая логическая форма… Все студенты должны сдавать экзамены. ^ Иванов – студент.

Поля аргументации ?????

Поле аргументации (ПА) — это занимаемая каждым субъектом индивидуальная или коллективная позиция, включающая множество относящихся к… (1) Суждения в ПА — это тезис и антитезис, а также все прямо или косвенно… (2) Способы аргументации — это используемые участниками приемы и методы обоснования и критики. Каждый субъект…

Согласование полей аргументации

Принципы согласования полей по основным компонентам: тезису и антитезису, аргументам, способам аргументации и фундаментальным позициям.

Несовместимость тезиса и антитезиса

Тезис и антитезис как несовместимые суждения должны находиться в свободных, непересекающихся частях ПА соответствующих субъектов, каждый из которых прилагает усилия убедить партнера и аудиторию принять его предложение.

Согласование аргументов

Принятие аргумента или согласие с ним может быть неявным, явным. Неявное, или слабое, принятие выражается в том, что партнер не возражает и тем… Если оппонент выражает несогласие или сомневается в достоверности аргумента, то пропонент может выбрать один из трех,…

Согласование способов аргументации

Способы аргументации, представляющие собой различные виды умозаключений, в форме которых протекают обоснование и критика, также согласовываются субъектами. В случае явного или молчаливого согласия партнеров способы аргументации считаются принятыми и включаются в пересечения полей трех субъектов.

Согласование фундаментальных позиций

[1] Абстракция (от латинского abstractio - отвлечение) - результат умственного отвле­чения от одних свойств познаваемых вещей и их свойств и… [2] В данной форме записи умозаключений черта означает слово «следовательно».… [3] Семантический треугольник Огдона и Ричардса приведен здесь с некоторым упрощением. Перевод терминов сделан в…