Модель сопряжения элементов

Математическая модель сложной системы помимо формального описания элементов обязательно включает формальные описания взаимодействия элементов – модель сопряжения.

В модели сопряжения элементов отражается не процесс функционирования элементов, а только такие их свойства, которые существенны для сопряжения элементов системы друг с другом и с внешней средой.

Основные предположения, концентрирующие интуитивные представления о закономерностях сопряжения элементов системы.

1. Взаимодействие между системой и внешней средой, а также между агрегатами внутри системы осуществляется посредством передачи сигналов, взаимное влияние вне механизма обмена сигналами не учитывается. Внешняя среда рассматривается как некоторый фиктивный агрегат, характеризуемый совокупностью входных и выходных сигналов.

2. Сигнал описывается конечным набором характеристик как совокупность элементарных сигналов, одновременно возникающих на входе элемента (аналогично и выходной сигнал). Любой сигнал можно характеризовать конечным числом параметров (для детали – размеры, материал, температура, для информационного сигнала – совокупность букв, цифр). Элементарные сигналы передаются независимо друг от друга по элементарным каналам. Каждому контакту соответствует один элементарный канал.

3. К каждому из входных контактов элемента подключается не более, чем один элементарный канал (исключается неопределенность в поведении элемента, если к нему будут приходить несколько элементарных каналов от различных выходных контактов).

Каждый элемент С_j, в том числе С₀, как элемент системы S достаточно характеризовать множеством входных контактов X₁^(j), X₂^(j), . . . , X_i^(j), . . ., X_m^(j), которое обозначим [X_i^(j)]₁^m, и множеством выходных контактов Y₁^(j), Y₂^(j), . . . , Y_k^(j), . . ., Y_r^(j), обозначаемым [Y_l^(j)]₁^r. Здесь для простоты приняты обозначения m = m_j, r = r_j.

Таким образом, математической моделью элемента С_j, используемой для формального описания сопряжения его с прочими элементами и внешней средой, является пара множеств [X_i^(j)]₁^m, [Y_l^(j)]₁^r.

Множество всех входных контактов всех элементов системы и внешней среды - 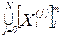. Множество выходных контактов - .

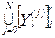Каждому входному контакту X_i^(j) соответствует не более чем один выходной контакт Y_l^(k), с которым он связан элементарным каналом. Поэтому можно ввести однозначный оператор

Y_l^(k) = R (X_i^(j)) с областью определений в множестве и областью значений в множестве , сопоставляющий входному контакту X_i^(j) выходной контакт Y_l^(k), связанный с ним элементарным каналом.

Совокупность множеств и 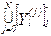и оператора R называется схемой сопряжения, оператор R – оператором сопряжения.

Оператор сопряжения можно задать в виде таблицы, в которой на пересечении строк с номерами элементов системы j и столбцов с номерами контактов i, располагаются пары чисел (k, l), указывающие номер элемента к и номер элемента l, с которыми соединен контакт X_i^(j).

На рисунках изображены пример агрегативной системы и оператора сопряжения в виде таблицы, возможная схема сопряжения подсистем агрегативной системы.

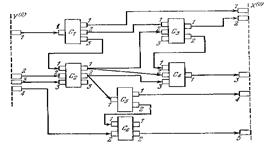
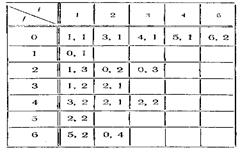
Возможная схема сопряжения элементов агрегативной системы и оператор сопряжения

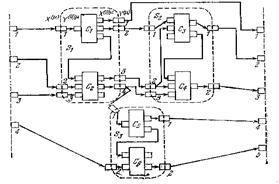Сложная система S может быть расчленена на некоторое число подсистем S_μ, μ = 1, 2, . . . , M, содержащих не менее чем по одному элементу таким образом, что данный элемент C_j входит только в одну из подсистем S_μ. Подсистема S_μ сама является сложной системой и в то же время – элементом системы S. Подсистема S_μ как самостоятельная система должна иметь контакты X_i^(0)μ и Y_l^(0)μ фиктивного элемента С₀^μ, представляющего внешнюю среду для нее, а как элемент системы S она должна содержать входные X_i^(μ) и выходные Y_l^(μ) контакты для связи с другими подсистемами. Соответствующие X_i^(μ) и Y_j^(0)μ, а также X_i^(0)μ и Y_l^(μ) объединяются в двойные контакты на границах подсистемы S_μ.

Возможная схема сопряжения подсистем агрегативной системы

Методика сопряжения связей между элементами сложной системы при помощи операторов сопряжения распространяется и на те случаи, когда в процессе функционирования системы структура связей изменяется во времени или подчиняется внешним командам управления. В этом случае в оператор сопряжения входит время t и параметр a (сигнал) управления.

5 МАТЕМАТИЧЕСКИЕ МОДЕЛИ ФИЗИЧЕСКИХ ЯВЛЕНИЙ И ПРОЦЕССОВ. универсальность моделей

5.1 Математические модели на основе фундаментальных законов

Математические модели, которые строятся на основе опытного изучения явления (феномена) – феноменологические модели. Эти модели связывают только непосредственно наблюдаемые и измеряемые в макро- опытах величины, физическая природа явления остается нераскрытой. Такие модели только описывают явления, устанавливают причинно-следственные связи, но не могут ответить на вопрос "почему?".

На феноменологической основе возникла первая крупная модель – механика Ньютона, подтвержденная экспериментальными данными. Он создал математическую модель и математически сформулировал один из фундаментальных законов природы – закон всемирного тяготения (в этом законе не ясна физическая природа сил тяготения).

Расширение феноменологической базы, накопление фактического экспериментального материала дает возможность создавать все более общие и полные модели (например, развитие механики от Ньютона к Эйнштейну).

Изучением математических моделей физических явлений занимается математическая физика. Для создания модели нет четких правил, но есть сложившийся набор приемов: учет основных фундаментальных законов, использование физических аналогий, вариационных принципов и т.д.

В физике сложилась схема построения моделей: формулируется система аксиом и совокупность правил, определяются допустимые операции над объектом, затем строится математическая модель. По мере накопления фактов модель уточняется, что дает возможность установить закономерности, предсказать течение процесса, его количественные характеристики в различных условиях.

При математическом описании физических явлений и процессов используются методы составления математических моделей: теоретический (на основе применения фундаментальных законов природы), эмпирический (экспериментaльно-стaтистический), экспериментaльно-aнaлитический (полуэмпирический), на основе аналогий, на основе вариационных принципов.

Эмпирические модели. Если процесс мало изучен и ничего не известно о его природе, используется эмпирический метод построения моделей. Этот метод тaкже позволяет получить мaтемaтическое описaние действующего объектa без исследовaния его внутренней структуры.

Построение эмпирических математических моделей основано на проведении экспериментальных исследований, связанных с наблюдением и измерением внешних проявлений свойств объекта, с последующим обобщением результатов этих измерений в алгоритмической форме или в виде аналитических зависимостей.

При построении эмпирических моделей используют понятие "черного ящика" – объект рассматривается безотносительно его внутренних свойств, т.е. без учета физической сущности протекающих в нем процессов (например, в метеорологии). Модель отрaжaет только зависимость значений выходных пaрaметров от входных.

На основании эксперимента строится приближенная модель. Подбираются аналитические зависимости, наилучшим образом согласующиеся с результатами эксперимента в точках их проведения: строится функциональная зависимость значений выходных параметров от входных.

Если такие модели построены без учета случайных ошибок (они отсутствуют или их статистические характеристики неизвестны), то приближенная модель называется эмпирической.

Если статистические характеристики случайных ошибок известны и учитываются, такая аппроксимирующая модель называется регрессионной. Уравнения регрессии строятся методом наименьших квадратов. Наиболее часто функцию представляют алгебраическими многочленами.

Экспериментально-аналитические модели - это смешанный тип математических моделей, в которых теоретические соображения качественного характера сочетаются с обработкой результатов наблюдений внешних проявлений свойств изучаемого объекта.

При использовании этого метода необходимо определить физическую сущность явлений, протекающих в объекте – в отличие от экспериментального, этот метод отражает теорию процесса. Для учета влияния явлений, не учтенных при составлении модели, вводятся эффективные коэффициенты на основе экспериментов.

Используется декомпозиция сложного явления, т.е. на основе анализа определяются более простые, элементарные процессы, которые можно исследовать более доступными способами.

После анализа влияния элементарных процессов на процесс в целом, несущественные факторы отбрасываются, и выбирается тот элементарный процесс, который оказывает наиболее существенное влияние. Затем для основного простого процесса составляется его математическое описание в виде характерной для этого процесса физической зависимости (не в форме полинома). Влияние остальных элементарных процессов учитывается изменением коэффициентов, входящих в эту зависимость.

Пример: процесс переноса тепла в неподвижном слое.

При определенных условиях (температура менее 800 К и малые линейные скорости потока газа) перенос тепла в основном определяется теплопроводностью и описывается уравнением Фурье (поток тепла пропорционален градиенту температуры): q_Т = - λdT/dx. Для учета всех составляющих процесса переноса тепла вводится экспериментальное значение коэффициента λ - некоторое "эффективное" значение λ_эф. Тогда уравнение примет вид: q_Т = - λ_эф dT/dx. Это уравнение является полуэмпирической моделью процесса переноса тепла в неподвижном слое. Коэффициент эффективности не является физической константой, a зависит от условий экспериментов, при которых она была получена и от масштабов установки.

На поверхности S тела с однородной по объему, но меняющейся во времени t температурой T(t) происходит теплообмен с окружающей средой, имеющей постоянную температуру T_с.

Примем, что плотность теплового потока от окружающей среды к телу пропорциональна разности температур q = α (T_с - T),где α - коэффициент теплоотдачи.

Подводимый к телу от окружающей среды тепловой поток

Q = qS = α (T_с - T)S.

Он вызывает изменение внутренней энергии тела, которое пропорционально скорости dT(t)/dt изменения температуры, а коэффициентом пропорциональности служит полная теплоемкость C_T тела, равная количеству тепловой энергии, необходимой для повышения температуры тела на 1К, измеряемая в Дж/K.

C_T dT(t)/dt = Q(t).

Скорость изменения температуры тела пропорциональна разности между температурой тела и температурой среды:

dT(t)/dt = к (T_с - T)S, к = α /C_T – коэффициент пропорциональности.

Матмодель, описывающая изменение температуры тела во времени – ОДУ первого порядка, решение которого при α = const имеет вид

T = T_с - (T_с – T₀) e ^{- αSt/CT},

где T₀ - температура тела в начальный момент времени t = 0.

Пример. Экспериментально-аналитическая модель (строится на основе теории процесса, коэффициенты определяются экспериментально) – коэффициент пропорциональности к определяется на основании эксперимента (с телом неизменного состава и поверхности).

Температура окружающей среды постоянна. Скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Из решения ОДУ (dT(t)/dt = - к (T_с - T), к – коэффициент пропорциональности):

ln (T – T_с) / (T₀ – T_с) = - kt.

Например, при температуре окружающей среды T₀ = 21 ⁰С, в течение часа температура тела снизилась с 31 до 29 С⁰. Тогда коэффициент пропорциональности к = ln (31 – 21)/(29 – 21) = 0,223. Зная к, можно определить время, за которое температура снизилась с 37 до 31 ⁰С:

T = 1/к ln (37 – 21)/(31 – 21) = 2,1 часа.

Эффективные коэффициенты изменяются в зависимости от условия проведения опытов, поэтому экспериментально-аналитическая модель справедлива лишь в том интервале, в котором производился эксперимент.

Теоретический метод составления математических моделей

При теоретическом методе мaтемaтические модели составляются на основе применения фундаментальных законов природы к конкретной ситуации.

На первый план здесь выдвигается неформализованный ответ на вопрос, какой закон (или законы) применять в каждом конкретном случае и как это делать.

На основе фундаментальных законов природы и аналогий выделяется класс общих моделей с достаточно высоким уровнем абстракции. Такие модели строятся, могут самостоятельно изучаться, анализироваться, дополняться доказанными свойствами и утверждениями. Сведения, полученные при теоретическом рассмотрении, применимы ко всем конкретным соответствующим системам.

Это фундаментальные законы сохранения, которые являются общими для материального мира: массы, энергии, количества движения, импульса, заряда (законы Архимеда, Ньютона, Кулона и др.), постулат о непрерывном движении материи, принцип наименьшего действия (механические процессы протекают так, чтобы произведение затрачиваемой энергии на время ее затрачивания было минимальным).