рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Движение тела переменной массы.
Реферат Курсовая Конспект
Движение тела переменной массы.
Движение тела переменной массы. - раздел Философия, МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ Дифференциальное Уравнение Поступательного Движения Твердого Тела, Масса Кото...
Дифференциальное уравнение поступательного движения твердого тела, масса которого зависит от времени, имеет вид
(mv) = F + v1 
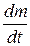, где F – главный вектор всех сил, действующих на тело, v1 – скорость присоединяющейся массы до присоединения (если dm/dt > 0) или скорость отделяющейся массы после отделения (если dm/dt < 0).
Ускорение w тела переменной массы w = 1/m(F + Fp), где Fp = (v1 – v)dm/dt = udm/dt – реактивная сила, равная произведению производной по времени от массы тела на относительную скорость u = v1 – v присоединяющейся или отделяющейся массы.
Пример. Движение ракеты в условиях отсутствия внешнего силового воздействия.
Реактивная сила, создаваемая двигателем, - сила тяги ракеты: Fp = u dm/dt, где dm/dt - скорость уменьшения массы ракеты за счет выгорания топлива.
Уравнение движения ракеты: m dv/dt = u dm/dt,
где v и m - скорость и масса ракеты в произвольный момент времени t, u - относительная скорость отделяющейся массы.
Векторы dv/dt и u направлены в противоположные стороны, потому m dv/dt = - u dm/dt, откуда при u = const следует уравнение Циолковского: v = v0 + ulnm0/m, где v0 и m0 - начальные значения скорости и массы ракеты (при t =0).
5.3 Уравнения состояния
Состояние тела определяется его внутренней энергией.
Термодинамическая система.
Термодинамической системой называется совокупность макроскопических объектов (тел и полей), обменивающихся энергией в форме работы и в форме теплоты как друг с другом, так и с внешней средой (внешними по отношению к системе телами и полями).
Состояние термодинамической системы определяется совокупностью значений ее термодинамических параметров (параметров состояния) – всех физических величин, характеризующих макроскопические свойства системы (плотность, энергию, вязкость, поляризацию, намагниченность и т.д.). Основные термодинамические параметры состояния – давление, температура и удельный объем.
Всякое изменение состояния термодинамической системы называется термодинамическим процессом. Изопроцессы – термодинамические процессы, протекающие при неизменном значении какого-либо параметра состояния. Состояние системы называется стационарным, если оно не изменяется во времени.
Термодинамический метод состоит в изучении свойств системы взаимодействующих тел путем анализа условий и количественных соотношений происходящих в системе превращений энергии.
Энергия системы, зависящая только от ее термодинамического состояния, называется внутренней энергией. Если система не подвержена действию внешних сил и находится в состоянии макроскопического покоя, внутренняя энергия системы является ее полной энергией.
Внутренняя энергия системы включает в себя энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и др.), энергию взаимодействия этих частиц, энергию электронных оболочек атомов и ионов, внутриядерную энергию и т.д.
Температура тела характеризует энергию, с которой движутся его молекулы, и характеризует состояние тела (является параметром состояния).
Внутренняя энергия является функцией состояния системы, т.е. зависит только от параметров состояния p, V , T и не зависит от способа, которым это состояние достигнуто.
Каждому термодинамическому состоянию системы соответствует определенное значение внутренней энергии.
Первый закон термодинамики: тепловая энергия, подведенная к замкнутой системе, расходуется на повышение ее внутренней энергии и работу, производимую системой против внешних сил.
Тепловая энергия (количество теплоты) представляет собой один из видов энергии и подчиняется закону сохранения энергии. Тепловая энергия может возникать в результате превращения других видов энергии (механической, электрической, химической и др.).
При нагревании амплитуда колебаний молекул увеличивается, расстояние между ними возрастает, и тело занимает больший объем.
Для твердого тела объемное расширение можно рассматривать как линейное расширение в трех направлениях.
В жидкостях при нагревании изменяется не только объем, но и плотность жидкости. Объем изменяется в соответствии с коэффициентом объемного расширения β: V2= V1(1 + β∆t). Объем и плотность жидкости обратно пропорциональны друг другу: ρ1/ ρ2 = V2/V1, тогда ρ2 = ρ1 / (1 + β∆t).
Газы расширяются значительно сильнее, чем твердые и жидкие тела. При постоянном давлении объем газа пропорционален абсолютной температуре, при постоянном объеме давление газа пропорционально абсолютной температуре (законы Гей-Люссака). Уравнение состояния идеального газа: pV = mRT (R – газовая постоянная). Газ считается идеальным, если для него при постоянной температуре выполняется равенство pV = const (закон Бойля-Мариотта). В реальних газах (вблизи токи конденсации – при высоком давлении и низкой температуре) свойства газа значительно отличается от идеального.
Упругие свойства твердых тел.
Ранее рассматривалось тело как материальная точка и абсолютно твердое тело. На самом деле внешние силы изменяют форму и объем реального тела – деформируют его. При деформации происходит относительное смещение элементов тела (его молекул). Деформации, исчезающие с прекращением действия силы, называются упругими. При превышении предела упругости в кристаллических решетках возникают необратимые изменения – происходит пластическая деформация тела. Тело не возвращается к исходной форме даже после прекращения действия внешних сил.
Внешние силы могут вызывать различные изменения тела – растяжение, сжатие, сдвиг.
Сила растяжения или сжатия, приложенная к стержню вызывает изменение длины тела - ∆x. Величина ∆x зависит от размеров стержня, материала, величины самой силы.
Закон Гука связывает линейную связи деформацию и механическое напряжение в упругом материале (упругие деформации прямо пропорциональны вызвавшим их воздействиям F = - kx).
Напряжение (σ = F/S, где F - сила, S – площадь поперечного сечения стержня) пропорционально поперечному сечению: σ = Еε, где Е – модуль упругости.
Механическое напряжение в продольном направлении кроме удлинения вызывают поперечное сжатие тела – с изменением длины тела изменяется и его поперечное сечение.
Относительное изменение поперечного размера тела εп = - με, где μ – коэффициент Пуассона.
Если к параллельным плоскостям тела приложены параллельные силы, направленные в разные стороны, то эти плоскости смещаются относительно друг друга. Такая деформация характеризуется углом сдвига. По аналогии с законом Гука, касательное напряжение τ = Gγ, G где – модуль сдвига, γ - сдвиговая деформация (угол сдвига).
Жидкости.
Жидкостями называются тела, которые имеют определенный объем, но не имеют упругости формы (отсутствие модуля сдвига). Жидкости отличаются сильным межмолекулярным взаимодействием и вследствие этого малой сжимаемостью. Вследствие подвижности молекул жидкость не обладает собственной формой, а принимает форму сосуда, поверхность жидкости всегда перпендикулярна действующей на жидкость силе.
Если на жидкость действует внешнее давление, то вследствие подвижности молекул это давление передается одинаково во все стороны.
Закон Архимеда. На погруженное в жидкость тело действует подъемная выталкивающая сила, направленная вверх и равная весу вытесненной телом жидкости: F = gVρ0, где V – объем тела, ρ0 - плотность жидкости.
Газы.
Молекулы газа практически не взаимодействуют друг с другом - в идеальным газе отсутствуют силы межмолекулярного взаимодействия (состояния, далекие от областей фазовых превращений). Поэтому газы не имеют формы и объема и целиком заполняют сосуд, в котором находятся.
Часто под внутренней энергией понимают только те ее составляющие, которые изменяются в рассматриваемых процессах. Например, при не слишком высоких температурах внутреннюю энергию идеального газа можно считать равной сумме кинетических энергий хаотического движения его молекул (тепловая энергия). Внутренняя энергия идеального газа зависит только от его абсолютной температуры и пропорциональна массе газа.
Для идеальных газов справедливы следующие законы.
Уравнение Клайперона-Менделеева (уравнение состояния идеального газа) о связи давления с плотностью и температурой: pV = RT, где p - давление, Vμ – молекулярный объем (объем, который занимает грамм-молекула), T – температура, R - газовая постоянная. Для произвольной массы М объем V = Vμ М/μ.
Закон Бойля-Мариотта: pV = const - при неизменной температуре и массе.
Закон Гей-Люссака: V = V0 T/T0 – при постоянном давлении объем данной массы газа прямо пропорционален его абсолютной температуре.
Закон Шарля: р = р0 T/T0 – при постоянном объеме давление данной массы газа прямо пропорционален его абсолютной температуре.
Закон Фурье: qt = - λ dT/dx – о связи плотности теплового потока и градиента температуры.
5.4 Универсальность моделей
Система может быть представлена в виде совокупности различных физически однородных подсистем, математическая модель каждой из которых описывает элементарные явления и процессы определенной физической природы (механические, гидравлические, тепловые, электрические) в основном в виде дифференциальных уравнений.
Большинство инженерных дисциплин можно рассматривать как упорядоченное множество математических моделей и расчетных схем – по существу, сложились базы данных математических моделей типовых элементов и расчетных схем.
При всем разнообразии объектов и систем, в которых протекают процессы различной физической природы, можно выделить отдельные блоки, модули, каждый из которых можно представить в зависимости от переносимой и преобразуемой физической субстанции можно рассматривать как механическую (поступательную или вращательную), электрическую, тепловую, гидравлическую (пневматическую) систему. При исследовании совокупности разнородных подсистем – автономно созданные модели объединяются в общую модель, внешние параметры одной подсистемы рассматриваются как функции переменных другой подсистемы.
Универсальность моделей – описание различных по своей природе процессов одинаковыми математическими моделями – позволяет использовать такую аналогию между различными процессами при построении сложных систем из типовых элементов.
В общем случае эти системы взаимосвязаны, но, используя принцип декомпозиции, их можно представить совокупностью типовых элементов, описываемых моделями макроуровня.
Модели на основе аналогий
Способ построения моделей с применением аналогий с уже изученными явлениями основан на предположении об универсальности моделей, т.е. приложимости их к объектам принципиально различной природы.
Например, предположение «скорость изменения величины пропорционально значению самой величины» широко используется в далеких друг от друга областях знаний.
У мaтемaтически подобных объектов процессы облaдaют различной физической природой, но описываются идентичными уравнениями.
Имеется ряд общих математически подобных моделей в физике, химии, биологии, экономике.
В простейших случаях используются известные аналогии между механическими, электрическими, тепловыми и другими явлениями.
Типичными для практического применения являются модели в виде наборов формул, систем линейных и нелинейных алгебраических и дифференциальных уравнений, дискретных переходов, статистических описаний, описании игровых ситуаций и т.д.
У мaтемaтически подобных объектов процессы облaдaют рaзличной физической природой, но описывaются идентичными урaвнениями.
Примеры различных по физической природе явлений и их мaтемaтические описания: в законах Фурье, Ньютона, Ома нaблюдaется подобие мaтемaтических описaний различных физических явлений. Поэтому любой из этих процессов с использовaнием определенных пересчетных коэффициентов может служить моделью другого процесса. Закон Ньютона притяжения двух материальных точек и закон Кулона взаимодействия двух точечных электрических зарядов при соответствующем выборе единиц измерения физических величин можно выразить одинаковыми формулами.
Закон Фурье: qt = - λ dT/dx Закон Ньютона: F = dK/dt
Закон Ньютона: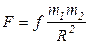 
Закон Кулона: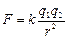 
Как видно, нaблюдaется подобие мaтемaтических описaний рaзличных физических явлений. Поэтому любой из перечисленных процессов может служить моделью другого.
Пример универсальности моделей – электрические схемы, процессы колебаний различной природы – несмотря на разную сущность объектов, им соответствуют одни и те же модели.
Воспроизводится не сам физический процесс, а его мaтемaтическое описание или аналогия между законами, которые одинаково выражают явление и в оригинале, и в модели. Процесс изучается на модели, в которой протекает другой по своей природе процесс, если мaтемaтические описaния этих процессов изоморфны (все свойства модели соответствуют свойствам оригинала).
Типовые математические модели элементов и подсистем
Большинство технических систем при всем их разнообразии обычно можно разделить на блоки, узлы, элементы, процессы в которых могут быть описаны функциональной математической моделью, отражающей физические, механические, химические, информационные процессы. Для каждого из таких процессов можно выделить типовые элементы, каждый из таких элементов можно рассматривать как электрическую, механическую поступательную или вращательную, тепловую, гидравлическую или пневматическую систему и представить математической моделью микроуровня.
В общем случае эти системы взаимосвязаны, но, используя принцип декомпозиции, их можно представить совокупностью простейших типовых элементов, и описывать систему моделями макроуровня.
Наиболее часто используются типовые элементы, описывающие колебательные процессы, электрические, гидравлические, пневматические, тепловые процессы.
При построении моделей типовых элементов удобно исследовать причины неадекватности моделей. Для выявления области адекватности модели иногда требуется рассмотрение модели микроуровня физических процессов в типовых элементах – обоснование области применения модели того или иного типа (линейной – нелинейной, статической – динамической и т.п.).
– Конец работы –
Эта тема принадлежит разделу:
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
Системность... Системные идеи лежат в основе деятельности человечества с начала его... Необходимость решения специфических проблем связанных с возникновением и развитием больших и сложных систем вызвала...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Движение тела переменной массы.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?
Подпишитесь на Нашу рассылку
Реклама
Информация в виде рефератов, конспектов, лекций, курсовых и дипломных работ имеют своего автора, которому принадлежат права. Поэтому, прежде чем использовать какую либо информацию с этого сайта, убедитесь, что этим Вы не нарушаете чье либо право.
© copyright 1999 - 2024 allRefs.net. Все права защищены. Страница сгенерирована за: 0.03 сек.
Новости и инфо для студентов