Модели элементов пневматических систем

Под пневматическими понимают технические системы, в которых рабочей средой является воздух или газ. Рабочая среда, в отличие от газа является сжимаемой: ее плотность r существенно зависит от давления р.

Газ называют совершенным, если для него справедливо уравнение Клайперона-Менделеева p = rRT, где T – температура газа, R - удельная газовая постоянная для данного газа. Тогда r = p/RT, масса m = rV = pV/RT.

В пневматической системе, как и в гидравлической, величиной, имеющей смысл потенциала, является разность (перепад) ∆р давлений. В качестве величины, характеризующей перенос рабочей среды, вместо объемного расхода рассматривается расход массы газа dm/dt.

При установившемся ламинарном течении по трубопроводу вязкого газа с постоянным расходом m' = ∆р V/RT или ∆р = m'R_п, R_п = const. Это линейное соотношение аналогично закону Ома ∆U = IR.

Для сосуда с фиксированным объемом V, газ выпускается (температура и плотность считаются постоянными) - масса газа изменяется во времени t. Тогда при T = T₀ получим соотношение

m' = dm/dt = V/RT₀ dp/dt = m₀/p₀ dp/dt = C_пdp/dt.

Это выражение аналогично выражению для электрического конденсатора I = Cd∆U /dt (C – емкость конденсатора).

Для участка трубопровода длиной l и площадью поперечного сечения S для идеального (невязкого) газа, движущегося с изменяющейся во времени скоростью v(t), в соответствии со вторым законом Ньютона (F = ma): S∆р = r S l dv(t)/dt или ∆р = L_пdm'/dt, что аналогично выражению для ЭДС идеализированной (без сопротивления) катушки: ∆U = LdI/dt (L – индуктивность катушки).

Соотношение ∆р = m'R_п можно считать справедливым при условии, что изменение давления по длине трубопровода вызывает пренебрежимо малое изменение плотности r газа. Тогда можно принять r= const, что означает постоянство объемного расхода газа V' = m'/r. Если трубопровод имеет круглое поперечное сечение радиуса r_*, то можно использовать выражение для гидравлического сопротивления при ламинарном течении вязкой несжимаемой жидкости R_г = 8ηl/π r_*⁴. В этом случае R_п = R_г/r.

В достаточно длинном трубопроводе изменение давления газа может оказаться существенным, что вызовет заметное изменение плотности газа. В этом случае при постоянном расходе массы m' газа по длине трубопровода его объемный расход V' по длине трубопровода будет переменным. По длине трубопровода может также меняться температура – тогда будет изменяться и плотность газа.

Как и в случае несжимаемой жидкости, при турбулентном режиме течения газа зависимость сопротивления трубопровода от расхода газа становится нелинейной.

 

 

6 МАТЕМАТИЧЕСКИЕ МОДЕЛИ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ В ИССЛЕДОВАНИИ ОПЕРАЦИЙ

6.1 Моделирование операций распределения ресурсов

При выборе концепции системы возникают задачи оптимального распределении имеющихся ресурсов системы – задачи выбора решений (способа действий) при целенаправленном функционировании системы. Это может быть организация взаимодействия элементов, определение оптимальных режимов функционирования системы в различных условиях внешней среды.

Такие задачи возникают при организации производства и снабжения, эксплуатации транспортных систем, параметров конструкции, выбора средств производства, вооружения, в здравоохранении, бытовом обслуживании, связи, при боевых действиях и т.д.

Любое целенаправленное действие называется операцией. В общем случае – это совокупность взаимосвязанных действий всех компонентов системы, направленных на решение поставленной задачи.

Модель операции (операционная модель - формализованное описание факторов и связей между ними, отражающих ход операции) представляет собой совокупность, состоящую из субъекта, формирующего цель операции (оперирующей стороны), запаса активных средств (ресурсов) для проведения операции, набора стратегий, т.е. способов использования этих ресурсов, и критерия для сравнения различных стратегий достижения цели операции.

Модель операции разрабатывается на основе схемы операции, представленной в виде ряда последовательных этапов и элементарных действий компонентов для решения поставленной задачи (выполнения цели системы).

Степень соответствия результата операции поставленной ей цели (задаче) характеризуется критерием эффективности, который может зависеть от всех факторов, входящих в модель операции, в том числе, и неопределенных.

И управления, и неопределенные факторы могут быть функциями различной природы и сложности в зависимости от конкретных условий проведения операции, информированности оперирующей стороны.

Основная задача исследования операций – принятие решения о наилучшем способе достижения цели - выбор программы действий (способов использования ресурсов на выполнение операции) – решается методами математического программирования.

Основные разделы теории исследования операций: математическое программирование (линейное и нелинейное, детерминированное и стохастическое), теория принятия решений и теория игр, теория управления запасами, теория массового обслуживания, имитационное моделирование. Выбор метода решения диктуют тип и сложность исследуемой математической модели.

Общая модель операции выработки решения состоит из взаимосвязанных моделей: модели процесса операции (включая модель управляемой системы и модель обстановки проведения операции) и модели принятия решения. При этом учитываются физические и критериальные ограничения.

Физические ограничения ни при каких обстоятельствах не могут быть нарушены, поскольку они выражают законы сохранения.

Пример физических ограничений. Обозначим через q_i норму полива – количество воды, которое мы должны направить на орошение единицы земельной площади x_i. Тогда

где Q - общее количество воды, которое накоплено в водохранилище.

Кроме того, суммарная площадь земли, которую можно использовать под посевы, также должна быть фиксирована, т.е. величины x_i должны удовлетворять еще одному ограничению:

где Х – суммарная земельная площадь.

Критериальные ограничения определяются требованиями к конструкции и не являются такими жесткими – они находятся в распоряжении субъекта и в принципе могут быть нарушены или изменены.

Например, распределяя землю под посевы, необходимо добиться урожая максимальной стоимости, но при заданной структуре конечного продукта, или при проектировании самолета, кроме достижения его максимальной экономичности, могут быть ограничения на его крейсерскую скорость (не меньше заданной).

Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями.

Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными.

Содержание математического программирования составляют теория и методы решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). В этом и состоит специфика задач математического программирования: множество условий задается не системой уравнений, а системой неравенств, чаще всего экстремум достигается на границах множества условий, где нарушается принцип дифференцируемости, в практических задачах число переменных столь велико, что приводит к необходимости применения аналитических методов или эффективных вычислительных способов получения приближенного решения.

Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием.

Классификация задач математического программирования.

В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса: задачи линейного и нелинейного программирования.

Линейное программирование – целевая функция линейна, а множество, на котором ищется экстремум целевой функции, задается системой линейных равенств и неравенств. В линейном программировании существуют классы задач, структура которых позволяет создать специальные эффективные методы их решения (например, транспортные задачи). Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования.

Нелинейное программирование – нелинейны целевая функция и ограничения. Здесь выделяют: выпуклое программирование (выпукла целевая функция и множество, на котором решается экстремальная задача), квадратичное программирование (целевая функция квадратична, а ограничения – линейные равенства и неравенства).

В математическом программировании могут быть выделены два направления – решение детерминированных (вся исходная информация определена) и стохастических задач (параметры носят случайный характер с известными вероятностными характеристиками).

 

Формулировка задачи математического программирования

Задачи математического программирования, как правило, содержат большое число переменных и ограничений и не всегда допускают умозрительный анализ. Здесь требуется тщательная формализация и включение в математическую модель всех сколько-нибудь существенных ограничений.

Прежде чем построить математическую модель задачи, необходимо четко разобраться с ситуацией, описанной в условии. Для этого необходимо с точки зрения заданной задачи, а не математики, ответить на следующие вопросы:

1) Что является искомыми величинами задачи?

2) Какова цель решения? Какой параметр задачи служит критерием эффективности решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов?

3) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.

После предварительной постановки задачи получают ее формальное решение для простейших случаев, на которых можно проанализировать корректность поставленной задачи. На основании такого анализа вводятся дополнительные параметры и ограничения, проверяется корректность отнесения задачи к тому или иному классу, корректность введения линейности.

Общая схема формализации на основании содержательного описания задачи:

1.Определение переменных задачи (основных параметров).

2. Определение управляющих переменных, характеризующих существо действий и их элементарных составляющих.

3. Формулировка критериев эффективности через параметры и управляющие переменные.

4. Определение ограничений (области допустимых решений) через переменные задачи.

Задача математического программирования содержит n переменных x_i (i=1, 2,. . . , n), образующих n-мерный вектор переменных х.

На переменные накладываются ограничения - в форме равенств h_i(x) = 0, i = 1, . . . , p или неравенств g_i(x) ≥ 0, i = 1, . . . , q.

f(x) – целевая функция (в общем случае нелинейная) всех или некоторых переменных x_i (i=1, 2,. . . , n).

Задача математического программирования формулируется следующим образом:

Минимизировать (или максимизировать) f(x) при условиях g_i(x) ≥ 0, i = 1, . . . , q; h_i(x) = 0, i = 1, . . . , p. Или кратко Min { f(x)│ g_i(x) ≥ 0, i = 1, . . . , q; h_i(x) = 0, i = 1, . . . , p}.

6.2 Модели линейного программирования

Линейное программирование применяется при решении задач оптимального распределения ресурсов, управления и планирования производства; определения оптимального размещения оборудования; оптимального плана перевозок груза (транспортная задача) и т.д.

Задачи линейного программирования - оптимизационные. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования.

Несмотря на различные области приложения, данные задачи имеют единую постановку:

найти значения переменных x₁, …, x_n, доставляющие оптимум заданной линейной формы z=c₁x₁ + c₂x₂+… + c_nx_n при выполнении системы ограничений, представляющих собой также линейные формы.

В задачах линейного программирования критерий эффективности и функции в системе ограничений линейны.

Если в задаче математического программирования имеется переменная времени, а критерий эффективности выражается через уравнения, описывающие течение операций во времени, то такая задача является задачей динамического программирования.

При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели свойств пропорциональности, аддитивности.

Основные допущения при построении линейных моделей:

- пропорциональность;

- аддитивность;

-. неотрицательность (не может быть отрицательного объема производства).

Пропорциональность - затраты ресурсов пропорциональны объему производства - вклад каждой переменной в целевой функционал и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной.

Например, если, продавая j-й товар в общем случае по фиксированной цене, фирма будет делать скидку при определенном уровне закупки до более низкого уровня цены, то будет отсутствовать прямая пропорциональность между доходом фирмы и количеством проданного товара. Т.е. в разных ситуациях одна единица j-го товара будет приносить разный доход.

Аддитивность означает, что целевой функционал и ограничения должны представлять собой сумму вкладов от различных переменных. Величина, соответствующая целому объему всегда равна сумме величин, соответствующих его частям при любом способе разбиения на части.

Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.

Решение практической задачи нельзя считать законченным, если найдено оптимальное решение. Некоторые параметры задачи (финансы, запасы сырья, производственные мощности и др.) можно регулировать, что, в свою очередь, может изменить найденное оптимальное решение. Эта информация получается в результате выполнения анализа чувствительности. Анализ чувствительности позволяет оценить влияние этих параметров на оптимальное решение. Если обнаруживается, что оптимальное решение можно улучшить за счет небольших изменений заданных параметров, то целесообразно реализовать эти изменения.

Формулировка общей задачи линейного программирования.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Каждая совокупность значений переменных (аргументов функции f), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция f, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции f, называется оптимальным планом задачи.

Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим образом:

Нужно определить максимум или минимум линейной целевой функции (линейной формы)

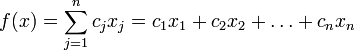
при ограничениях в виде равенств или неравенств

, i = 1, . . . , r;

, i = r+1, . . . , g;

, i = g+1, . . . , m;

x_ij ≥ 0 - требование неотрицательности управляющей переменной

где x_j, j=1, . . ., n – управляющие переменные, или решения задачи,

b_i, a_ij, i=1, . . ., m, j=1, . . ., n – параметры,

f – целевая функция.

Задача содержит n переменных и m ограничений.

Множество точек, удовлетворяющих системе ограничений, называется допустимым множеством (областью). Любая точка этого множества называется допустимой точкой (решением, планом). Линейная функция называется целевой функцией. Допустимая точка, которая минимизирует (максимизирует) функцию цели, называется оптимальным планом – решением задачи линейного программирования.

Вканонической форме задача является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х₁, х₂, ..., х_n являются неотрицательными.

Естественным решением сформулированной задачи линейного программирования является метод простого перебора: найти произвольное решение х₁ в допустимой области, вычислить (с, х₁), затем найти другое решение х₂, вычислить (с, х₂) и т.д. и среди полученных значений целевой функции (с, х) выбрать наименьшее. Этот путь перебора оказывается нереализуемым в связи со сложностью поиска допустимых решений, (допустимая область решений имеет бесконечное множество точек) и невозможностью поиска всех допустимых решений. Для решения задач линейного программирования строятся такие схемы поиска, которые позволяют выбирать оптимальный план, не перебирая всех возможных вариантов.

Типовые задачи линейного программирования

Методы линейного программирования позволяют описать широкий круг задач коммерческой деятельности, таких, как: планирование товарооборота; размещение розничной торговой сети города; планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных перевозок товаров (транспортная задача); распределение работников торговли по должностям (задача о назначении); организация рациональных закупок продуктов питания (задача о диете); распределение ресурсов; планирование капиталовложений; оптимизация межотраслевых связей; замена торгового оборудования; определение оптимального ассортимента товаров в условиях ограниченной площади; установление рационального режима работы.