рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
Реферат Курсовая Конспект
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ - раздел Философия, 1 Методологические Основы Моделирования Сложных Систем 1.1 Системнос...
1 МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
1.1 Системность
Системные идеи лежат в основе деятельности человечества с начала его зарождения, но формулироваться и широкого распространяться начали с середины XX века - объекты стали рассматриваться как множества взаимосвязанных элементов (как системы), во взаимодействии с другими системами.
Необходимость решения специфических проблем, связанных с возникновением и развитием больших и сложных систем, вызвала к жизни множество приемов, методов, подходов, которые постепенно накапливались, развивались, обобщались, образуя, в конце концов, определенную технологию преодоления количественных и качественных сложностей.
Системные технологии вместе с их теоретическими основами получали разные названия: «методы проектирования», «методы инженерного творчества», «системотехника», «исследование операций»;
В начале 80-х годов 20 века уже стало очевидным, что все эти теоретические и прикладные дисциплины образуют как бы единый поток, «системное движение».
Системность предполагает представление об объекте любой природы как о совокупности элементов, находящихся в определенном взаимодействии между собой и с окружающим миром, а также понимание системной природы знаний. Системность - способ видения объекта и стиль мышления.
На этой основе (системность мира) формулируется общая методология системных исследований - набор методологических подходов (принципов) к исследованию системы - системный подход.
Сложные системы любого вида функционируют в сложном взаимодействии между собой и не поддаются адекватному описанию в рамках одной научной дисциплины - исследования таких систем имеют междисциплинарный характер и требует системного мышления. При системных исследованиях задача сводится к использованию наработанных методов и процедур других дисциплин: исследования операций, теории информации, теории принятия решений и др.
Исследование операций – предполагает выбор наилучшего решения поставленной системе задачи. Сложившаяся методология исследования операций - построение модели (формализованная схема функционирования системы, описание факторов и связей между ними, отражающих ход операции), постановка оптимизационной задачи и ее решение.
Менеджмент экономический определяет функции управления, что включает постановку целей, принятие решений и контроль их выполнения. Объектом экономического моделирования является вся экономическая сфера, включающая экономическую теорию, экономическую политику и хозяйственную практику. При решении этих задач естественно опираться на системные исследования и математическое моделирование.
Проблема организации управления может быть сформулирована как оптимизация децентрализации и передачи полномочий другим уровням на основе получаемой информации - возникла необходимость имитационного моделирования. Для сложных технических систем с управлением необходимо моделирование функционирования самой системы во внешней среде, прогнозирование возможных результатов управления. Управление вырабатывается на основе исследований процессов в системе (модели системы с учетом технических, технологических, социальных и прочих факторов).
Дифференциация науки привела не только к углублению научного знания об объекте, но и к ослаблению связей, прежде всего информационных между различными областями науки – возникла необходимость привлечения знаний из разных наук, что привело к возникновению междисциплинарных исследований, которые выступают в качестве средств установления связей между, отношений между различными объектами.
Стало возможным исследование объектов как таковых, их связей, отношений. Науками о специфических видах отношений являются, в частности, теория игр (изучает отношения конфликта), кибернетика (изучает отношения управления – рассматриваются управляющие системы, причем конкретный носитель управления значения не имеет).
Понятия общей теории систем
Специальные научные дисциплины представляют собой модели определенных сторон действительности. Всем системам, вне зависимости от их физической природы, присущи определенные общие закономерности, отношения между элементами.
Попытка выявить некоторое основание, объединяющее все науки, приводят к мысли о необходимости построения общей теории систем, задачей которой стала бы формулировка некоторых принципов образования, развития, функционирования любых реально существующих систем.
Любая теория должна быть основана на предположении о существовании достаточно общих законов. Учитывая широту понятия системы, для теории систем эти законы должны быть чрезвычайно общими, граничащими с философскими, и в то же время приложимыми к практике - приближающими теорию к точным наукам.
Понятия общей теории систем должны быть настолько общими, чтобы охватывать все реально существующие проблемы, и вместе с тем обеспечивать возможность получения адекватной информации о рассматриваемом явлении. Чем выше общность теории, тем меньше возможность получения такой адекватной информации. Этим теория систем отличается от общепринятого понятия теории - нет строгого определения системы, так же как нет достаточно полных определений понятий элемента системы, структуры системы, связи.
С попытками построить общую теорию систем возник вопрос: существует ли система реально, или она привносится в действительность человеком?
Исходя из того, что прерогатива выделения системы, элементов системы принадлежит человеку, возникла тенденция: система существует не в природе, а в сознании людей – наш мозг накладывает некую структуру на реальное бытие, выделяя тем самым систему.
Бир: система «представляет собой нечто, обнаруживаемое и понимаемое нами, когда она отображается в нашем сознании».
Система не произвольная конструкция сознания – в сознании отражается объективная действительность. Исследователь в процессе познания вычленяет определенную структуру объекта и придает ей то значение, которое он считает необходимым для отражения взаимосвязей ее элементов.
Таким образом, система как некоторое теоретическое представление об объекте не существует вне нашего познания и практики, хотя сам объект существует объективно: существуют реальные объективные системы (объекты) и системы понятий (мысленные, концептуальные системы), которые характеризуют этот объект.
Возможна и другая интерпретация, при которой «системность» рассматривается именно как принцип, неотделимый от теоретических установок субъекта - наблюдателя, его способности представить, сконструировать объект познания как системный: система, структура, окружающая среда не существуют в природной или социальной реальности, а формируются в нашем знании в результате операций различения и конструирования, проводимых наблюдателем. При этом реальность должна обладать такими «параметрами», которые могут быть представлены как системы.
Соответственно складывается особый язык, включающий прежде всего такие общенаучные понятия, как системность, отношение, связь, элемент, структура, часть и целое, целостность, иерархия, организация, системный анализ и многие другие.
Принцип системности понимается как универсальное положение о том, что все предметы и явления мира – это системы различных типов и видов целостности и сложности. Задача субъекта-исследователя - обнаружить систему, ее связи и отношения, описать, классифицировать объяснить их.
Принцип системности объединяет несколько идей и представлений: системности, целостности, соотношения части и целого, структурности и «элементарности» объектов, универсальности, всеобщности связей, отношений, развития.
На этой основе (системность мира) формулируется общая методология системных исследований - набор методологических подходов (принципов) к исследованию системы - системный подход.
Пример. Системные исследования в области экологии.
Методологической основой исследований в области экологии является комплексное использование натурных экспериментов, измерений и исследований, экспе6риментальных лабораторных исследований, применения методов управления и моделирования, широкое использование методов других наук (химии, физики, геологии, математики и др.).
Эти методы можно объединить в несколько групп:
- методы регистрации и оценки качества окружающей среды, прежде всего различные типы экологического мониторинга (дистанционный аэрокосмический мониторинг, биомониторинг и биоиндикация);
- методы количественного учета организмов и методы оценки биомассы и продуктивности растений и животных;
- изучение особенностей влияния различных экологических показателей на жизнедеятельность организмов (длительные наблюдения в природных и лабораторных условиях – токсикологические, биохимические, биофизические, физиологические и др.);
- методы изучения взаимосвязей между организмами в многовидовых группах;
- методы математического моделирования экологических явлений и процессов, а также экосистем, имитационное моделирование, моделирование локальных, региональныхи глобальных экологических процессов и ситуаций;
- создание геоинформационных систем и технологий для решения экологических вопросов различных масштабов в разных сферах деятельности;
- комплексный эколого-экономический анализ состояния различных объектов, территорий, отраслей производства;
- геоэкологические методы исследований, геоэкологический мониторинг с целью уменьшения негативного влияния загрязнений на окружающую среду;
- технологические методы экологизации различных производств с целью уменьшения негативного влияния загрязнений на окружающую среду;
- медико-экологические методы изучения влияния различных воздействий на здоровье людей;
- методы экологического контроля окружающей среды (экологические экспертиза, аудит, паспортизация и т.д.).
Определение понятия системы
Определение понятия системы – это тоже модель (лингвистическая) наших представлений о системе. В такой постановке понятия системы и модели системы… Различные системы, встречающиеся в природе и обществе, имеют различное… Пример живых организмов. Простейшими их элементами служат клетки. Последние образуют подсистемы, называемые тканями,…Взаимодействие и взаимозависимость системы и внешней среды.
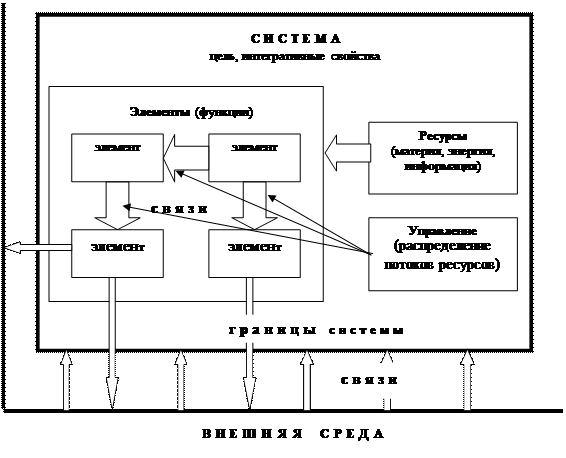
Определение понятий элементов, связей, функций, внешней среды системы.
Элемент
Элемент системы – целостный объект (материальный, энергетический, информационный), неделимый для данной системы, выполняющий в системе определенные функции.
Это часть системы, выделенная по какому-либо признаку, сформулированному заинтересованным лицом (исследователем системы).Для того чтобы компонент стал элементом системы, обеспечивающим ее интегративные свойства, он должен иметь входы и выходы, совместимые с другими элементами, видоизменять поток ресурса, который обеспечивает выполнение требуемых функций, не разрушаться под действием ресурса.
В элементах системы входы (вещественные, энергетические информационные) преобразуются в выходы - осуществляются связи элементов между собой и с внешней средой, обеспечивающие выполнение функций в соответствии с целями системы.
Элементы, передаваемые системой во внешнюю среду, могут быть конечными продуктами деятельности системы, а передаваемые из среды в систему — ресурсами.
Выбор, какие компоненты в данной системе считаются элементарными, относительно произволен и в большой степени оставляется на усмотрение исследователя. Низший уровень для одного исследователя может оказаться достаточно высоким для другого.
Основной признак, по которому элемент вводится в систему – функциональный. Удаление элемента из системы неизменно влечет за собой изменение ее целей (интегративного свойства). Ответ на вопрос, включать или не включать элемент в систему зависит от его необходимости для функционирования системы.
Целостность системы не может быть нарушена. Система, лишенная какого либо элемента, теряет интегративное свойство, перестает быть системой, поскольку элемент и был включен в систему, чтобы она выполнила это интегративное свойство (автомобиль без бензина или без колеса не поедет – это будет уже другое состояние системы).
Неделимость элемента – это понятие, а не физическое свойство. Членение системы в общем случае не имеет предела, поскольку и элемент может рассматриваться как система.
Элемент является лишь условно неделимой частью. Условность состоит в том, что, при изменении задач исследований элемент может быть также разделен, или, наоборот, объединен с другими элементами в один.
Элементы в системе могут быть разнородными, отличаться по принципу действия, функциям. Состав компонентов системы может быть гомогенным (содержать однотипные элементы), гетерогенным (содержать разнотипные элементы) и смешанным. Система может включать вещественные, энергетические, информационные элементы.
Сами по себе элементы не представляют никакого интереса: только в процессе взаимодействия элементов реализуется система – в этом случае они выступают как элементы системы.
Связи
Связи системы определяют порядок обмена между элементами системы веществом, энергией, информацией.
Связи объединяют элементы в целостную систему (внутренние связи) и обеспечивают взаимодействие системы с внешней средой (внешние связи).
Упорядоченность отношений между элементами системы – внутренних устойчивых связей, которые, преобразуя выходы одних компонентов во входы других, обеспечивают ее функционирование, предполагает наличие структуры системы.
В зависимости от задачи исследований один и тот же компонент можно представлять как связь или как элемент (например, провода).
Связи характеризуются физическим наполнением (вещественные, энергетические, информационные, смешанные), направленностью (прямые, обратные), мощностью (мощность связей между элементами системы больше мощности связи этих же элементов с внешней средой).
Связи управления обеспечивают распределение ресурса между элементами для выполнения интегративного свойства.
Реальные связи между компонентами системы являются очень сложными и различной природы, имеют различный характер влияния на ход процессов в системе. В искусственных системах существенную роль играют экономические и социальные связи. При оценке информационных связей необходимо учитывать качественные характеристики информации – ценность, достоверность и др.
Внутренние связи формируют структуру системы и преобразует выходы одних компонентов во входы других.
Связь выступает в виде воздействия – ее можно определить как физический канал, по которому обеспечивается обмен веществом, энергией, информацией. Основная особенность связи – преобразование некоторой величины вещества, энергии, информации без изменения их физической природы. Под влиянием внешних воздействий система может перейти в одно из своих возможных состояний или разрушиться.
Чтобы совокупность элементов стала системой, их нужно структурировать и заложить в систему интегративное свойство - необходимо определенным образом структурировать связи (обеспечивающие потоки ресурсов) и нанести на них информацию (направления потоков).
Различаются прямые и косвенные связи – непосредственное взаимодействие между элементами и взаимодействие между элементами через систему.
Физические системы не просто находятся в окружении, они существуют благодаря окружению, и успех функционирования системы определяется ее совместимостью с окружающей средой. Изменение свойств внешней среды влияет на выполнение системой своих функций, функционирование системы влияет на внешнюю среду.
Мощность экономических связей может быть оценена финансовыми обязательствами, объемами поставок и т.д.
Мощность информационных связей оценивается величиной потока информации. Потенциальная мощность системы – ее пропускная способность. При оценке мощности информационных связей необходимо учитывать качественные характеристики передаваемой информации – достоверность, полезность, ценность и т.п.
Мощности функциональных связей можно оценить через коэффициент чувствительности изменения функций системы в зависимости от мощности воздействий.
Задание связей
При моделировании для определения отношений между элементами системы, между системой и окружающей средой необходимо точно установить причинно-следственные связи. Причинно-следственные связи могут быть детерминированными и вероятностными.
Входные воздействия (входы) - воздействия на элемент (вещества, энергии, информации) со стороны внешней среды (других элементов).
К входам относятся функционально обусловленные воздействия, необходимые для реализации цели системы (например, управляющие воздействия), и возмущающие воздействия.
Выходные воздействия (выходы) - воздействия со стороны элемента на другие элементы системы или внешнюю среду.
К выходам относятся результаты работы системы (обеспечивают реализацию цели системы), и вынужденные (вредные выбросы) воздействия.
Выходы элемента определяются входами и внутренним строением элемента: выход есть функция от входа и самого элемента.
Понятия входа и выхода переносится на любую совокупность элементов: группа элементов может характеризоваться только входами и выходами всей группы, не описывая, как связаны между собой ее элементы.
Построение математической модели предполагает установление зависимостей между внешними, внутренними и выходными параметрами. Модели систем, как правило, многоуровневы.
Внешняя среда
Объекты, принадлежащие одной подсистеме, можно рассматривать как составляющие внешней среды другой подсистемы. Изменение свойств внешней среды влияет на выполнение системой своих функций,… Границы системы определяются при выделении системы из внешней среды исходя из целей функционирования системы: в…Функции системы
Функции компонента определяются собственными свойствами компонента и его связями с другими компонентами. Между функциями компонентов имеются связи… Для сложных систем поведение системы представляется алгоритмом, записанным в… Параметры системы - это величины характеризующие качество, свойства или режимы работы объекта. Различают выходные,…Системный подход
Такой подход основывается на признании того, что если даже каждый элемент или подсистема имеет оптимальные конструктивные или функциональные… Шеннон: «Архитектор может рассматривать дом вместе с его электрической,… Системный подход предполагает рассматривать объект как сложно организованную систему, состоящую из множества…Классификация систем
Классификация - разделение всех изучаемых объектов на отдельные группы в соответствии с каким-либо важным для исследователя признаком.
При классификации различные понятия и соответствующих им явления объединяются в определенные группы, типы с целью установления связей между объектами и классами объектов.
Становление каждой науки связано с созданием классификаций изучаемых объектов, явлений.
Классификация - это процесс упорядочивания информации. В процессе изучения новых объектов в отношении каждого такого объекта делается вывод: принадлежит ли он к уже установленным классификационным группам. В некоторых случаях при этом обнаруживается необходимость перестройки системы классификации.
Классификационные методы позволяют свести многообразие фактов к сравнительно небольшому числу образований (классов, типов, форм, видов, групп и т.д .), разработать систему соответствующих понятий и терминов, обнаружить регулярности, устойчивые признаки и отношения, в конечном счете – эмпирические закономерности, подвести итоги предшествующих исследований и предсказать существование ранее неизвестных объектов или их свойств , вскрыть новые связи и зависимости между уже известными объектами.
В естественных науках представлены как описательные классификации, позволяющие просто привести к удобному виду накопленные результаты, так и структурные классификации, позволяющие выявить и зафиксировать соотношения объектов. Так, в физике описательные классификации – это деление фундаментальных частиц по заряду, спину, массе, по участию в разных типах взаимодействий.
Методологические проблемы классификаций: несовпадение формальных условий и правил построения классификаций и реальной практики.
Требование дискретности признаков порождает в ряде случаев искусственные приемы разбиения целого на дискретные значения признаков; не всегда возможно вынести категорическое суждение о принадлежности объекту признака, при многоструктурности признаков ограничиваются указанием на частоту встречаемости и т.д.
Известно немало примеров удачных классификаций, но никто не владеет рецептом построения удачной классификации.
Классификация – неформализуемый процесс, выполняется итеративно: концептуальное описание классов (содержательная постановка), выделение существенных свойств или функций (что может быть не одно и то же), уточнение и т.д., при этом в основу могут быть положены прототипы (как по свойствам, так и по функциям).
Агрегирование в классы – нетривиальная процедура. Класс может рассматриваться как результат действия оператора вида: «ЕСЛИ <условия на агрегируемые признаки>, ТО <имя класса>. Класс может задаваться совокупностью признаков.
Основная проблема классификации – допустимая минимизация описания системы или явления. При декомпозиции эта проблема решается компромиссом при определении понятия существенности применительно к целям исследований – возникает риск недостаточной полноты или излишней подробности. При агрегировании риск неполноты становится недопустимым (описали не то, что необходимо для исследований) – требуется установить перечень минимальных свойств, учет которых необходим для заданных исследований (определить конфигуратор).
Примеры классификаций - таблица Менделеева, классификации животных, растений и т.д. Для представителей живой природы установлена определенная градация: класс, отряд, род, вид, вариация.
Классификации представляются в виде схем, таблиц, используемых для ориентировки в многообразии понятий или соответствующих объектов.
Нечеткость понятия системы, многообразие систем приводят к неопределенности принципов классификации, уровней деления. Полной классификации систем нет и не может быть.
В основу классификации могут быть положены различные принципы: происхождение систем, сложность, целевой характер, типы управления, свойства и др.
Классификация моделей и видов моделирования объектов и систем должна выделить в них наиболее общие признаки и свойства реальных систем.
В силу многозначности понятия «система» в науке и технике не существует единой классификации видов систем.
По своим свойствам системы могут быть классифицированы по следующим признакам.
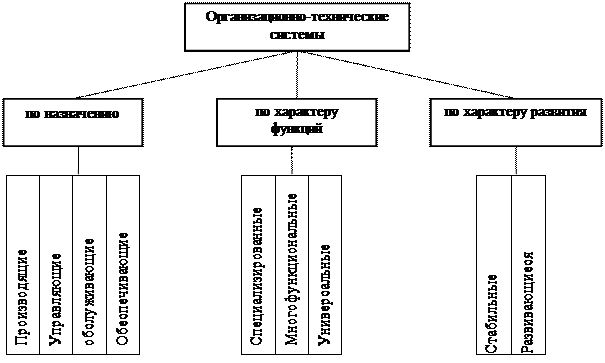
* По назначению: производящие (реализуют процессы получения некоторых продуктов и услуг), потребляющие (по отношению к производящим), управляющие (организуют и управляют вещественными, энергетическими или информационными процессами), обслуживающие (поддержание заданных пределов работоспособности обслуживаемых систем и восстановление работоспособности при ее утрате), обеспечивающие системы (создают надлежащие условия эксплуатации и использования обеспечиваемых систем).
* По характеру функций: специализированные (единственность назначения), многофункциональные (набор нескольких функций в одной и той же структуре), универсальные системы (разнообразный набор функций в одной и той же структуре для решения широкого круга задач, не всегда заранее определенного).
* По характеру развития: стабильные и развивающиеся системы (изменяются или не изменяются свойства, структура и функции системы за весь период существования).
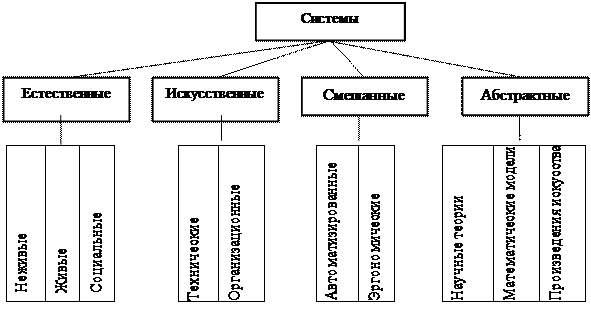
* По происхождению: естественные, искусственные, смешанные, абстрактные системы, каждая из которых может быть разделена по различным принципам.
Пример двухуровневой классификации систем по происхождению (природной принадлежности):
Естественные (природные): неорганические, биологические, экологические, другие.
Искусственные: материальные, абстрактные (идеальные), абстрактно-материальные.
Смешанные: организационно-технические, социально-экономические, другие.
* Организационные системы - системы, содержащие активные элементы (подсистемы), которые имеют возможность самостоятельно принимать решения относительно своего состояния.
В организационных системах структура реализуется в виде совокупности персонала, методов, алгоритмов, технических устройств различного назначения.
При появлении новых задач и, соответственно, функций может оказаться необходимой корректировка структуры. После создания системы возможно уточнение ее структуры и отдельных функций в рамках существующих целей и задач, т.е. возможно обратное влияние структуры на функции.
* Экономические системы - системы, в которых действуют стоимостные или натуральные товарные переменные. В качестве экономической системы может выступать отдельная фирма; техническая или технологическая система, учитывающая стоимость технических средств или продукции; отрасль промышленности; экономика государства.
Экономическая система, в которой действуют социальные факторы, называется социально-экономической. В частности, любая макроэкономическая система государства или региона не может не включать социальный сектор и поэтому является социально-экономической.
 | ||
 |
Возможны классификации по следующим свойствам.
По характеру связей с внешней средой:
Закрытые системы — какой-либо обмен энергией, веществом и информацией с окружающей средой отсутствует. Имеют четко очерченные, жесткие границы. Для их функционирования необходима защита от воздействия среды.
Открытые системы обмениваются с внешней средой энергией, информацией и веществом. Обмен с внешней средой, способность приспосабливаться к внешним условиям является для открытых систем непременным условием их существования.
По характеру эволюции:
Динамические системы – эволюционируют с течением времени, параметры изменяются со временем, в статических – не изменяются.
Примеры динамических систем: биологические, экономические, социальные системы; такие искусственные системы как завод, предприятия, поточная линия и т.д.
По степени определенности: разделяются на детерминированные и вероятностные (стохастические) системы. В детерминированной системе по ее предыдущему состоянию и некоторой дополнительной информации можно вполне определенно предсказать ее последующее состояние. В вероятностной системе на основе такой же информации, можно предсказать лишь множество будущих состояний и определить вероятность каждого из них.
По характеру входных воздействий и внутренних состояний системы:
непрерывные и дискретные, линейные и нелинейные, стационарные и нестационарные, детерминированные и стохастические.
Для линейных систем реакция на сумму двух иди более различных воздействий эквивалентна сумме реакций на каждое возмущение в отдельности, для нелинейных – это не выполняется.
Если свойства системы изменяются во времени, то она называется нестационарной, противоположным понятием является понятие стационарной системы. Пример нестационарных систем – это системы, где процессы, например, старения являются на данном интервале времени существенными.
Если вход и выход системы измеряется или изменяется во времени дискретно, через шаг t, то система называется дискретной. Противоположным понятием является понятие непрерывнойсистемы. Например: ЭВМ, электронные часы, электросчетчик – дискретные системы; песочные часы, солнечные часы, нагревательные приборы и т.д. – непрерывные системы.
Могут быть использованы и такие основания классификации – экологические, социальные и искусственные системы.
Экологическая система– это весь материальный мир обитания человека, обеспечивает жизнедеятельность живой материи на Земле и состоит из физических, химических и биологических систем.
Физические системыобеспечивают различные взаимодействия тел и полей, что является непрерывным процессом строительства всего мироздания. Механизмами взаимодействия, функционирования и управления этих систем являются объективные физические законы.
Химические системыосуществляют непрерывный обмен веществ в природе, их преобразование и транспортировку из внешней среды в биологические системы и обратно. Источниками развития этих систем являются вещества; механизмами функционирования – законы физики и химии.
Биологические системы координируют жизнедеятельность всех организмов и их отдельных органов, рост организма, строение, размножение, приспособление к внешней среде и т.д. Источником развития биологических систем являются физические, химические и в том числе и сами биологические системы вселенского пространства.
Социальные системы– это реальный мир, в котором живет человек (общество, государство, этнос, коллектив, семья, нация, институты, религия, искусства и т.д.). В этих системах люди, взаимодействуют друг с другом, создают механизмы и законы жизнеобеспечения. Роль социальных систем заключена в формировании мировоззрения, сознания, культуры, системы человеческих взаимоотношений. Социальные системы формируют модели поведения человека.
Искусственные системы – это системы, созданные человеком в результате научно-технического прогресса. Они предназначены для повышения эффективности труда, его механизации, автоматизации и кибернетизации. Источниками “жизнедеятельности” этих систем являются все виды систем, перечисленные выше.
Современный уровень развития науки позволяет говорить о мире как о бесконечной иерархической системе систем, находящихся на разном уровне иерархии и разных стадиях развития.
Развитие искусственной системы и ее жизненный цикл
Возможны различные причины возникновения в системе противоречий (проблем): изменение целей, изменения условий внешней среды, проникновение в систему… В зависимости от проблемы и возникших условий возможны как эволюционные… Развитие возникает в результате необходимости снятия противоречий как внутри системы (структурные – между потоками…Жизненный цикл системы - это непрерывный процесс развития и существования системы с момента принятия решения о необходимости ее создания до момента ее полного изъятия из эксплуатации.
В процессе жизнедеятельности система проходит ряд взаимосвязанных этапов развития, отличающихся друг от друга формами взаимодействия со средой. Различают два генеральных периода жизненного цикла системы - развитие системы и целевое функционирование системы, каждый из которых характеризуется специфическим комплексом процессов – этапами жизненного цикла.
Жизненный цикл системы представляет собой достаточно сложную упорядоченную во времени совокупность взаимосвязанных процессов. Эти процессы пересекаются, и определить время всего жизненного цикла как сумму процессов невозможно. Жизненному циклу системы присущи все свойства систем – целостность, иерархичность структуры.
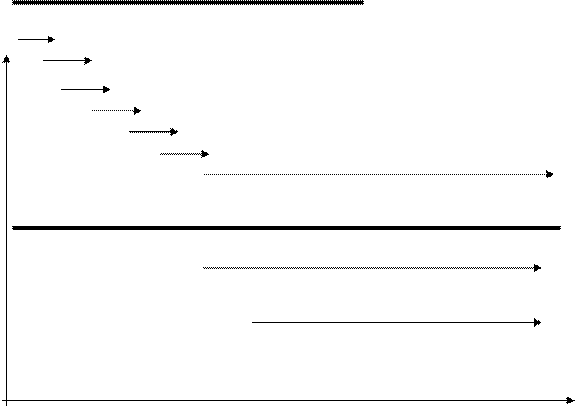 Развитие
Развитие
Формирование концепции
Техническое предложение
Эскизное проектирование
Техническое проектирование
Изготовление рабочей документации
Экспериментальная отработка
Изготовление
Целевое функционирование и деградация
Функционирование
Восстановление функциональных характеристик, сохранение уровня эффективности
t
1.2 Моделирование
Моделирование как отражение реальной действительности зародилось вместе с человеком – от наскальной живописи, сказок, кукол, ритуальных танцев, сотворения идолов, карт звездного неба, календаря и т.п. и т.п. - до составления систем сложных математических моделей.
Модельные методы познания появились уже в средние века – появилось понимание, что, изучая что-то на одном объекте (например, на человеке – анатомию, кровообращение), можно обобщить полученные знания на все подобные объекты.
Новые задачи требуют новых моделей.
Пример – модель солнечной системы как отражения реальной действительности. Геоцентрическая модель Птолемея для мореплавания давала способы расчета положения планет на небосводе. Затем появилась гелиоцентрическая модель Коперника, которая в сочетании с работами Кеплера позволила заменить модель Птолемея.
Модель в широком понимании – отражение действительности, понятие модели относится к любым знаниям и представлениям о реальном мире.
Искусство отражает окружающий мир, пытаясь создать ассоциации и передать эмоции, чувства.
Наука намного примитивнее, она грубо упрощает реальное, выделяя ограниченную группу явлений и полностью игнорируя остальные. Но это и создает основное преимущество науки – точность и универсальность результатов. Операции с объектами, описанными четкими определениями и аксиомами можно вести очень точно и единообразно. Здесь главное – освоение искусственных приемов, с помощью которых реальность отражается в ее абстрактные образы (приближенные эквиваленты). Полученные результаты исследований правомерны только в пределах применимости принятых определений и аксиом (изменение аксиомы о параллельных прямых в геометрии Евклида приводит к построению геометрии с новыми свойствами – геометрии Лобачевского).
Моделирование как способ познания
Понятие модели (как и понятие системы) не имеет строгого формального определения, допускается много различных трактовок в зависимости от целей моделирования и классификаций моделей (классификация как структурная форма наших представлений о предмете также является моделью).
В наиболее общем виде можно сформулировать следующие основные положения.
Модель (лат. modus - масштаб, способ действия, фр. modиle – образец) – это материальный или абстрактно представленный объект, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства. При этом отражаются наиболее существенные закономерности ее структуры и процесса функционирования, непосредственно изучается не сам интересующий нас объект, а некоторая вспомогательная искусственная или естественная система (модель), которая находится в некотором объективном соответствии с познаваемым объектом, обеспечивает изучение некоторых свойств оригинала;
Модель может выступать как в виде вещественного агрегата или физического процесса, так и в абстрактном виде, в знаковой форме – математическая модель.
Важнейшей особенностью любой модели является ее сходство с оригиналом в одном или нескольких из строго зафиксированных и обоснованных отношений.
Модель в широком понимании – отражение действительности, понятие модели относится к любым знаниям и представлениям о реальном мире.
Модель дает упрощенный образ, отражающий не все свойства прототипа, а только те, которые существенны для исследования.
Моделирование как способ познания предполагает перенос знания, полученного при анализе модели, на оригинальный объект. Прогресс развития науки и техники определяется возможностью познания - способностью создавать модели явлений, объектов.
Реальное моделирование подразделяется на натурное и физическое.
Натурное моделирование - проведение исследования на реальном объекте с последующей обработкой результатов эксперимента с целью выявления закономерностей протекания реального процесса.
Физическое моделирование отличается от натурного тем, что исследование проводится на установках, которые сохраняют природу явлений и обладают физическим подобием с реальным объектом. В процессе физического моделирования задаются некоторые характеристики внешней среды и на установках исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях внешней среды.
Существует много подходов к классификации методов и приемов моделирования.
По способу представления различают три основных вида моделей: описательные (словесное содержательное описание), натурные (макеты, физические модели - изучаемые свойства объекта представлены этими же свойствами, но в другом масштабе), знаковые модели (символьное - представление величин и отношений между ними с помощью букв, чисел, знаков, символов).
В классической физике, механике 17 – 18 веков получили дальнейшее развитие две главные ветви моделирования как способа познания – технико-экспериментальная и теоретическая. Пришло понимание, что математическая формулировка физических законов - это модель реального мира. С углублением познания мира уточняется математическая формулировка законов.
Первой системой математических моделей, адекватно отражающих обширный класс процессов и явлений реального мира, стала классическая механика. Одной из основных задач классической механики была задача прогнозирования движения различных тел и сред. Любая модель механического движения представляет собой систему дифференциальных уравнений относительно координат и скоростей движущегося объекта – из необходимости моделирования и прогнозирования движения возникло дифференцмальное исчисление.
Таким образом, модель есть материально или теоретически созданная система, предназначенная заменить или представлять объект исследования в процессе познания. Модель должна быть более удобной для исследования. Изучение модели позволяет получить информацию о реальном объекте исследования.
Модель обычно служит средством, помогающим в объяснении, понимании или совершенствовании системы. В частности, оно обозначает копию предмета, служащую для его изучения.
Модели могут применяться как средства:
- анализа (изучения) характеристик и поведения реальных объектов в различных условиях;
- синтеза (создания) объектов с требуемыми характеристиками, заданным поведением;
- обучения и тренировки (тренажеры);
- общения (язык, письменность).
При обучении с помощью моделей достигается высокая наглядность отображения различных объектов и облегчается передача знаний о них. Это в основном модели, позволяющие описать и объяснить систему.
В научных исследованиях модели служат средством получения, фиксирования и упорядочения новой информации, обеспечивая развитие теории и практики.
В управлении модели используются для обоснования принимаемых решений. Такие модели должны обеспечить как описание, так и объяснение и предсказание поведения систем.
При экспериментировании с моделью сложной системы можно получить больше информации о внутренних взаимодействующих факторах системы, чем при манипулировании с реальной системой благодаря изменяемости структурных элементов, легкости изменения параметров модели и т.д.
Польза от моделирования может быть достигнута только при соблюдении достаточно очевидного условия: модель адекватно отображает свойства оригинала, существенных с точки зрения цели исследования.
Модель и моделирование нужны для того чтобы:
- понять, как устроен конкрентный объект: какова его структура, внутренние связи, основные свойства, законы развития и взаимодействия с окружающей средой;
- научиться управлять объектом или процессом, определять наилучшие способы управления при заданных целях и критериях;
- прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект.
Три составные части проблемы моделирования:
- построение модели (эта задача наименее формализуема - нет алгоритмов построения моделей);
- исследование модели (эта задача более формализуема - имеются методы исследования различных классов моделей);
- использование модели.
Когда системы становятся сложными, то их теория практически заключается в том, чтобы найти пути их упрощения. Теория систем по сути представляет собой теорию упрощений.
Связь понятий модели и информации
Модель можно рассматривать как детализацию и конкретизацию системы, т.е. понятия системы и модели можно рассматривать как два последовательных звена в цепи упрощения и схематизации объекта исследования.
Информация — это абстракция.
Модель — это тот объект, та система, которая позволяет облечь эту информацию в конкретное, например компьютерное, представление, содержание.
Моделирование — тот процесс, метод, который позволяет осуществлять перенос информации от реальной системы к модели и наоборот.
Определение понятия моделирования во многом зависит от определения понятия информации, понимания места моделирования среди методов познания.
Любой материальный объект имеет набор свойств. Свойства объекта выявляются (а могут и не выявиться) в процессе взаимодействия объекта с другими объектами, т.е. в результате установления некоторого отношения между объектами (например, чтобы определить цвет объекта необходимо иметь источник света и анализатор цвета – дальтоник цвета определить не может, но это не значит, что объект его не имеет). Свойства объекта могут изменяться во взаимодействии с другими объектами и с внешней средой, или изменять свойства других объектов и внешней среды.
Объект несет в себе информацию, но получить ее можно, отразив в другом объекте: единство материи и информации – материя без информации не проявляется, информация без материи невозможна.
Многие из свойств могут быть описаны количественно (например, состав, масса, цвет, прочность и др. – число их огромно).
Модель называется изоморфной (одинаковой по форме), если между нею и реальной системой наблюдается полное поэлементное соответствие.
Такое соответствие имеется между негативом и полученным с него изображением, чертежом и изготовленной по нему деталью, между процессами в реальной системе и уравнением, описывающим поведение этой системы.
Во многих случаях изоморфные модели оказываются сложными и неудобными для практического использования, поэтому более удобны модели, которые позволяют судить только о существенных аспектах поведения реальных систем без их детализации. Пример такой модели — географическая карта по отношению к изображенному на ней участку земной поверхности.
Модели, отдельные элементы которых соответствуют лишь крупным частям реальной системы, а полное поэлементное соотношение между моделью и системой отсутствует, называются гомоморфными.
Например, карта, глобус предоставляют некоторую информацию о местности, причем, объем информации зависит от целей, которые поставили при создании карты, глобуса.
Вся информация, которая содержится в одном объекте, никогда не может быть полностью отображена в другом объекте. Количественное отображение информации является отображением объекта – его моделью, которая может быть представлена как мера снятия неопределенности отображения объекта (определяется целями отображения).
Пример карты: полную информацию о местности может предоставить сама местность. Винер: наилучшей моделью кота может быть другой кот, а еще лучше – тот же самый кот.
В большинстве случаев исследуется не сама система (сложность, громоздкость, недоступность), а формализованное описание (модель) тех ее свойств, которые существенны для целей исследований, т.е. процесс познания зависит от поставленной цели.
Сущность объекта проявляется в виде свойств, которые имеют информационную природу, информация – это свойства объекта (системы), отображаемые во взаимодействии с субъектом.
Количественное отображение информации является отображением объекта – его моделью, которая может быть представлена как мера снятия неопределенности отображения объекта (определяется целями отображения).
Поскольку сущность объекта проявляется в его свойствах, а описать свойства во всех мыслимых условиях (которых бесконечно много) невозможно, то полностью познать объект практически невозможно - невозможно создать исчерпывающую его модель.
С развитием исследований больших и сложных систем (изучение функционирования, управления, проектирования) пришло понимание того, что применение интуитивно выбранных моделей может привести к тому, что полученная информация об объекте в рамках целостной системы может быть недостаточной или даже ошибочной.
Появилась тенденция сведения всех изолированных моделей одного и того же объекта в одну систему моделей или системную модель. Понимание же того, что такую единую модель невозможно построить, привело к возникновению науки, объединяющей абстрактные понятия системности с практикой - «системного анализа».
Каждая изолированная модель, представляющая какое-то свойство объекта, должна в такой системной модели занять определенное место, соответствующее месту свойства реального объекта, которое было смоделировано. Здесь моделирование выступает как средство решения задач системного исследования.
Общая методология моделирования
Выделение общих принципов, подходов к построению и исследованию моделей является предметом методологии моделирования. Создание единой теории моделирования (и проектирования) систем весьма проблематично.
Методология – исходные руководящие принципы, способы и формы деятельности.
Общих правил построения моделей для различных дисциплин и задач практически не существует – нет единой теории систем, теории моделирования (и не может быть – достаточно высокий уровень обобщения приводит к формулировке общефилософских принципов).
Могут быть обобщены только некоторые общие схемы и принципы построения моделей в различных областях знаний, на основе которых разрабатываются конкретные правила и рекомендации по построению частных моделей в конкретных предметных областях.
Специальная методология – совокупность методов, приемов, способов построения моделей в конкретной области, основывается на законах этой конкретной области.
Несмотря на то, что создание любой новой модели – процесс творческий, близкий к искусству, существуют достаточно общие подходы, методы, «инструменты», пригодные для различных предметных областей.
Моделирование – искусство, интуиция, основанная на опыте·.
Проблема описания (моделирования) материального мира сводится, прежде всего, к описанию причинности всех реальных движений материи.
Фактически все разделы механики, физики, химии посвящены построению и исследованию математических моделей различных физических объектов и явлений.
Понятия модели как нечто универсальное, как способ исследования технических систем начали складываться в исследовании операций, кибернетике, информатике, системном анализе, затем и в других областях науки и техники. Все эти (и другие) дисциплины исследуют не саму систему, а ее модель, и в каждой из этих дисциплин сложились присущие им подходы к построению математических моделей.
При построении модели обычно учитываются только наиболее существенные для достижения поставленных целей моделирования факторы - построенная модель не тождественна объекту-оригиналу.
Однако неучтенные факторы в совокупности могут приводить к существенным различиям между объектом и его моделью, что приводит к необходимости отладки или оптимизации построенной модели после ее апробации на тестовых примерах.
Если результаты дальнейшего моделирования удовлетворяют исследователя и могут служить основой для прогнозирования поведения или свойств исследуемого объекта, то говорят, что модель адекватна объекту - оригиналу. При этом адекватность модели конкретному объекту зависит от целей моделирования. Построение идеально адекватной модели принципиально невозможно из-за практической невозможности учета большого числа параметров объекта-оригинала.
Основной принцип построения моделей: свойства объекта исследуются на модели, сходство которой с объектом существенно, а различие несущественно (здесь главным становится вопрос о степени существенности сходства модели и объекта).
Моделирование как метод исследования имеет следующую структуру: постановка задачи, создание модели, исследование модели, перенос знания с модели на оригинал.
Использование того или иного метода исследований определяется характером стоящих перед исследователем задач. Рассмотрение внутренних механизмов функционирования объекта, взаимосвязей и взаимодействий его с внешней средой обуславливает применение системного подхода.
Основные принципы моделирования
Информационная достаточность - наличие определенного порогового уровня априорных знаний о системе, когда существуют условия построения модели, адекватной исследуемой системе и целям ее исследования. Моделирование системы бессмысленно, если имеется исчерпывающая информация о ее функционировании.
Осуществимость - модель должна обеспечить достижение цели исследования за определенное (конечное) время.
Множественность моделей - для исчерпывающего исследования моделируемого явления, объекта, процесса создается набор моделей для исследований с разных сторон и с разной степенью детализации.
Агрегирование модели в соответствии с агрегированием моделируемой системы на подсистемы (агрегаты). Это дает возможность при необходимости перестраивать модель системы в зависимости от проблем и задач исследования, возникающих в отдельных подсистемах.
Параметризация – при необходимости упрощения модели или недостатке исходных данных в общей модели системы модели подсистем могут быть заменены некоторым обобщенным параметром и его соответствующими числовыми значениями (или графиками, таблицами, формулами), что даст возможность не описывать их функционирование.
Целевой характер моделирования
Таким образом, моделирование имеет целевой характер - модель отображает не вообще оригинал, а то, что необходимо для исследований системы. Модель, абсолютно эквивалентная действительности есть только идеализация.… В моделях достаточно потребовать не эквивалентности их оригиналам, а выделения из полного набора свойств тех свойств…Процесс моделирования
В основе общей методологии – сочетание методов анализа и синтеза. Синтез заключается в создании описания объекта, анализ – в определении свойств… Единство анализа и синтеза относится ко всем отраслям знаний, в т.ч. к… АнализЦели математического моделирования
Из этого следует множественность моделей одного объекта: для каждой цели требуется своя модель одного и того же объекта (множественность моделей… Моделирование имеет целевой характер - модель отображает не вообще оригинал, а… Каждая система существует или создается, чтобы реализовать определенную цель. Те переменные, которые не связаны по…Задание математических соотношений
В самом общем виде модель может быть представлена в виде схемы:
 |
Здесь:
X - вектор входных переменных;
Y - вектор выходных переменных;
F - оператор модели, обеспечивающий преобразование входных переменных в выходные в соответствие с задачей, решаемой системой.
Алгоритмы – совокупность операторов, задаваемая с помощью конечной системы правил.
Совокупность правил, образующих алгоритм, должна обладать следующими свойствами:
- полнота: в процессе решения задачи не может возникнуть ситуация, для которой отсутствует указание относительно дальнейших действий;
- однозначность: каждое правило, образующее алгоритм, можно понимать лишь единственным образом;
- непротиворечивость: предписания алгоритму не должны противоречить или взаимоисключать друг друга;
- массовость: возможность использования алгоритма на всем множестве возможных численных значений исходных величин;
- результативность: способность для любых допустимых исходных величин получать результат за конечное число шагов.
Примеры алгоритмов: алгоритмы функционирования (совокупность предписаний, ведущих к выполнению какого либо процесса в системе), алгоритмы управления (совокупность предписаний, определяющих характер воздействия органа управления на исполнительные органы для выполнения ими заданного алгоритма функционирования), алгоритмы контроля, информационно-поисковые и др.
Возможный способ записи алгоритмов - с помощью операторных схем, содержащих пронумерованную последовательность операторов, каждый из которых отображает элементарные операции (группу операций).
Модульное построение моделей
Модуль - группа элементов системы, описываемая только своим входом и выходом. Вместо термина модуль зачастую используются термины "блок", "подсистема" и др.
Синонимы понятия «модуль»: в технике – «узел», «механизм», «блок»; в программировании – «программа», «программный модуль», «логический блок»; в организации – «подразделение».
Разбиение системы на взаимодействующие модули (подсистемы) зависит от цели исследования и может иметь различную основу, в том числе может иметь материальную (вещественную), функциональную, алгоритмическую, информационную и др. основу. Разбиение системы на модули способствует более эффективной организации анализа и синтеза систем, так как оказывается возможным, абстрагируясь от второстепенных деталей, уяснить суть основных соотношений, существующих в системе и определяющих исходы системы.
Примером систем, у которых при разбиение на подсистемы вещественная, функциональная и информационные основы слиты, являются системы управления оргсистемами.
Модули можно рассматривать как преобразователи потоков (материи, информации, энергии), циркулирующих в рассматриваемом объекте.
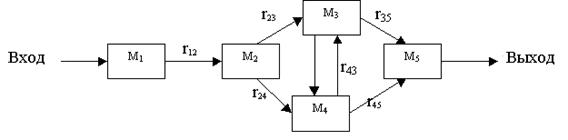
Отношения инцидентности связывают выход одного модуля со входом другого и обеспечивают их согласованность. Для этого бывает достаточно преобразовать данные одного типа в данные другого типа (осуществить перевод с одного "языка" на другой).
Декомпозиция системы на взаимодействующие модули (подсистемы) зависит от цели исследования и может иметь материальную (вещественную), функциональную, алгоритмическую, информационную и др. основу (пример – организационные системы). При этом осуществляется согласование отдельных модулей, их входов и выходов.
Структура полученной сложной модели должна соответствовать структуре и иерархии исходной системы, точнее, полученная модель должна быть адекватной исходной модели для принятых целей исследований.
 |
XВН – внешние воздействия;
XЭ – воздействия (связи) от других элементов модуля М на систему;
УВН - воздействия (связи) от элементов модуля на внешнюю среду (не-систему);
УЭ - воздействия (связи) от элементов системы на другие элементы системы.
Связи X-М можно рассматривать как часть Uj функции U, которая реализуется модулем М.
Разбиение системы на модули способствует более эффективной организации анализа и синтеза систем, так как оказывается возможным, абстрагируясь от второстепенных деталей, уяснить суть основных соотношений, существующих в системе и определяющих исходы системы.
Простейшая модель модуля – модель "черного ящика".
В модели "черного ящика" рассматривается объект, о котором известны только зависимости выходов от входов, - описываются только внешние связи и функции (оклик системы на внешние воздействия). Такая модель не рассматривает внутреннее устройство системы - нет информации о составляющих объект элементах, то есть неизвестны его Х-параметры. Поэтому функция объекта записывается в упрощённом виде, как его реакция на внешние воздействия.
Формальная запись модели «черного ящика» в виде преобразования:
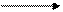 ({ XВН}, {XЭ}, М) ({УВН}, {УЭ}).
({ XВН}, {XЭ}, М) ({УВН}, {УЭ}).
Трудность построения математических моделей "черного ящика" состоит в том, чтобы определить, какие реальные связи из бесчисленного множества необходимо включить в модель. Тот факт, что мы не включили в модель остальные связи, не лишает их реальности – они все равно воздействуют на систему независимо от того, включили мы их в рассмотрение, или нет. Критерием включения связи должны служить цели исследования, существенность той или иной связи по отношению к этим целям (неформальная задача).
Исследуя поведение модели "черного ящика", описывающей систему, т.е. изменяя некоторым определенным образом входные воздействия и исследуя влияние этих изменений на выходы, можно достигнуть такого уровня знаний свойств системы, который позволит предсказать изменение ее выходных параметров при любом изменении входных параметров в исследуемом диапазоне.
Однако, как бы детально не изучалось поведение "черного ящика", мы никогда не сможем понять его внутреннее устройство, поскольку одну и ту же реакцию на внешние воздействия могут иметь различные системы с различным внутренним строением. Поэтому изучение системы методом "черного ящика" принципиально не может привести к выводу о ее внутреннем строении, поскольку поведение ее не отличается от поведения изоморфных ей систем.
Этот метод широко применяется в тех случаях, когда представляет интерес поведение системы, а не ее строение (например, при исследовании сложных управляемых систем). Модель "черного ящика" часто оказывается единственно применимой для исследований - исследование живого организма, отсутствие данных о строении системы (исследование электрона).
Понятие вариационных принципов
Вариационные принципы представляют собой общие утверждения об объекте (системе, явлении) и гласят, что из всех возможных вариантов поведения (движения) выбираются лишь те, которые удовлетворяют определенным условиям. Обычно это достижение экстремального значения некоторой величины при переходе из одного состояния в другое.
Например: законы преломления оптики, движение автомобиля по пересеченной местности – выбирается путь, требующий минимальной затраты времени.
Вариационные принципы уточняются по мере развития человеческих знаний.
В основе вариационных принципов положен анализ соотношения таких философских категорий, как возможность и действительность.
Действительные движения, путь, энергия или другие характеристики материальных систем отличаются от многообразия возможных, но не реализующихся движений – действительные значения могут быть представлены как экстремальные случаи из всех мыслимых.
Классическая механика основывается на законах Ньютона, установленных для свободных материальных точек, и аксиомах связей – справедливость принципов доказывается исходя из этих аксиом. С другой стороны, любой из принципов можно принять за аксиому и из нее логически вывести законы механики.
Дифференциальные уравнения движения, все положения и законы механики могут быть получены как следствие некоторых более общих положений – вариационных принципов механики. Законы сохранения эквивалентны вариационным принципам и поэтому могут рассматриваться как следствие последних.
В качестве основных моделей механики могут рассматриваться не только дифференциальные уравнения, связывающие параметры движения в данный момент, но также некоторые общие свойства, характеризующие движение механической системы в целом на любом произвольном отрезке времени - вариационные принципы, математически выраженные в форме вариационных соотношений из которых как логические следствия вытекают дифференциальные уравнения движения и все положения и законы механики. Построение моделей с помощью вариационных принципов по своей широте и универсальности сопоставим с возможностями, даваемыми фундаментальными законами.
Законы сохранения эквивалентны вариационным принципам и поэтому могут рассматриваться как следствие последних.
Один из вариационных принципов - принцип минимума рассеяния (диссипации) энергии (природа как бы выбирает наиболее экономный способ достижения цели).
Принцип минимума рассеяния (диссипации) энергии – из всех возможных траекторий перевода системы из одного состояния в другое реализуются лишь те, для которых затраты энергии минимальны. Выбирается такая траектория, двигаясь по которой система в максимальной степени поглощает энергию – траектория минимального рассеяния энергии.
Принцип диссипации энергии строго не доказан.
Принцип устойчивости: реализуются лишь устойчивые формы движения (неустойчивые формы если возникают, то быстро разрушаются·).
Принципы устойчивости и диссипации энергии в ряде случаев могут быть противоречить друг другу – иллюстрация закона единства и борьбы противоположностей.
Например, две формы движения жидкости – и ламинарное и турбулентное движения удовлетворяют законам сохранения. Если количество жидкости Q, протекающее через трубу в единицу времени мало, то реализуется устойчивый ламинарный режим. Он более экономичен, затраты энергии минимальны. Если ввести какое-либо возмущение, оно быстро затухнет. При Q > Qкрит ламинарный режим становится неустойчивым – реализуется турбулентный режим, как отвечающий принципу диссипации, которому отдается предпочтение перед принципом устойчивости.
Разнообразию уровней обобщений явлений в каждом конкретном случае исследований соответствуют различные формы и модификации вариационных принципов.
Вариационные принципы механики, характеризующие свойства движения, по форме подразделяются на дифференциальные принципы – характеризуют свойства движения для любого данного момента времени, и интегральные принципы - характеризуют свойства движения на любых конечных промежутках времени.
2.3 Требования к построению модели
Требования к модели определяются исходя из ее основного свойства - модель должна обладать существенными признаками объекта моделирования и быть работоспособной.
Принципы и подходы к построению математических моделей
Принципы определяют те общие требования, которым должна удовлетворять правильно построенная модель. Рассмотрим эти принципы.
1.Модель должна строиться для конкретной цели исследования системы (явления, процесса) и соответствия ей точности результатов моделирования. Полнота модели должна предоставлять исследователю возможность получения необходимого набора оценок характеристик системы с требуемой точностью и достоверностью.
Попытки создания универсальной модели, нацеленной на решение большого числа разнообразных задач, приводят к такому усложнению, что она оказывается практически непригодной. Строить модель, приближающуюся по сложности к реальной системе не имеет смысла.
2. Исходя из целей исследований выбираются основные свойства системы для детального их рассмотрения. Детализация модели определяется необходимой точностью решения задачи для достижения цели исследования.
Менее существенные свойства игнорируются (абстрагирование от второстепенных деталей, не оказывающие влияния на решение поставленной задачи) - упрощение при сохранении существенных свойств системы.
3. Блочная структура модели и минимальные связи между блоками с учетом разделения модели по этапам и режимам функционирования системы. Это дает возможность использования накопленного опыта в процессе отработки модели и многовариантной реализации блоков, отличающихся по точности и сложности, - построения ансамбля моделей.
При получении новой информации об объекте его модель пересматривается и уточняется, т.е. процесс моделирования является итерационным. Этот итерационный процесс продолжается до тех пор, пока не будет получена модель, которую можно считать адекватной в рамках решения поставленной задачи исследования и проектирования системы.
Адекватность и достоверность модели
Модель адекватна (adaequatus – приравненный) объекту, если результаты моделирования удовлетворяют исследователя по заданной степени точности и могут служить основой для прогнозирования поведения или свойств исследуемого объекта. Адекватность модели зависит от целей моделирования и принятых критериев оценки выполнения целей.
Предпочтительна та модель, которая, позволяя достичь желаемых результатов, является более простой. При этом адекватность и простота не являются противоречивыми требованиями.
Для объекта любой сложности, можно предположить существование множества его моделей, различающихся по степени полноты, адекватности и простоты. Учитывая заложенную при создании неполноту модели, можно утверждать, что идеально адекватная модель принципиально невозможна.
Адекватность - качественное и количественное совпадение именно тех характеристик модели с объектом, которые важны в данном конкретном случае, и в той мере, в которой это достаточно для достижения цели исследования (степень соответствия действительности предсказаний, сделанных на основе модели исходя из целей моделирования).
Оценка адекватности математической модели – определяется степень соответствия результатов, полученных по разработанной модели, данным эксперимента или тестовой задачи.
Модель, адекватная при анализе одних характеристик, может быть неадекватна при анализе других.
Вопрос, что является для данной модели существенным, а что нет, решается неформально на основе качественного анализа и с помощью количественных вычислений при проверке модели.
Требование реализуемости модели заставляет сокращать число учитываемых факторов за счет их ранжирования по степени влияния на адекватность модели, что осуществляется при решении каждой конкретной задачи на каждом уровне.
Забвение того, что всякая адекватность математической модели реальному объекту лишь относительна и имеет свои рамки применимости, может привести к грубым ошибкам, основанным на бесконтрольном приписывании реальному объекту свойств его модели.
В сложных случаях мы можем говорить об адекватности лишь с некоторой долей уверенности. Эта уверенность повышается, если следствия из принятой модели хорошо согласуются с надежно установленными фактами или физическим экспериментом.
Говоря о математической модели и ее адекватности, часто не упоминают о том, какие именно свойства объекта моделируются. При этом нельзя забывать о принципиальной ограниченности области возможного применения любой математической модели.
Качественная адекватность модели (адекватность функционального описания) - соответствие характера реакции системы и модели на изменения входных параметров. Качественная адекватность предполагает оценку совпадения с экспериментальными данными вида функции (убывающая или возрастающая, с одним или несколькими экстремумами).
Понятию качественной адекватности близко понятие достоверности.
Достоверность (полнота) модели: отражение в достаточной мере именно тех характеристик и особенностей моделируемого объекта, которые соответствуют поставленной цели исследования.
Для оценки достоверности необходимо выявить: что известно точно (достоверно), что – с оцениваемой степенью неопределенности (например, с известной вероятностью для стохастических моделей), что можно считать достоверным только при выполнении определенных условий, что известно о том, что неизвестно.
С одной стороны, при создании модели необходимо обеспечить способность модели отображать свойства системы истинно, полно и точно, с другой стороны – обеспечить простоту, умеренную сложность модели для ее приемлемой реализуемости. Эти противоречивые требования решаются неформально - в зависимости от поставленной задачи.
Требование достоверности вынуждает строить модель как можно более полную, точную – учитывать больше факторов на каждом уровне, увеличивать количество уровней иерархии.
С понятием достоверности связано прежде всего понятие упрощенности моделей – приближенностью отображения действительности. Величину, меру, степень приемлемости различия можно ввести только соотнося его с целью моделирования. Пример: различная точность часов для различных целей.
Количественная адекватность модели - соответствие количественных характеристик тем частным случаям, для которых уже имеются фактические данные или апробированные на практике модели – соответствие выходов модели и объекта при одинаковых условиях с заданной точностью. Количественная адекватность модели (мера адекватности) оценивается в зависимости от заданной точности решения задачи (определяется целью исследований) - осуществляется оценка принятых гипотез и допущений для различных начальных условий. Модель считается адекватной, если она отражает заданные свойства объекта с приемлемой точностью (с относительной погрешностью не более некоторого заданного значения).
Понятия достоверности и адекватности являются условными, поскольку мы не можем рассчитывать на полное соответствие модели реальному объекту, иначе это был бы сам объект, а не модель. Поэтому в процессе моделирования следует учитывать адекватность не модели вообще, а именно тех ее свойств, которые являются существенными с точки зрения проводимого исследования. В процессе проверки модели необходимо установить включение в модель всех существенных факторов. Сложность решения этой проблемы зависит от сложности решаемой задачи.
Адекватность модели может не удовлетворять исследователя по многим причинам: из-за идеализации внешних условий и режимов функционирования; исключения тех или иных параметров; пренебрежения некоторыми случайными факторами. Отсутствие точных сведений о внешних воздействиях, определенных нюансах структуры системы, принятые аппроксимации, интерполяции, предположения и гипотезы также ведут к уменьшению соответствия между моделью и системой. Это приводит к тому, что результаты моделирования будут существенно отличаться от реальных.
Простейшей мерой адекватности может служить отклонение некоторой характеристики 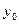 оригинала и
оригинала и 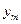 модели,
модели,
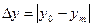 или
или 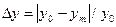
Понятие адекватности включает в себя понятия устойчивости и точности модели.
Устойчивость математической модели - изменение в определенных пределах параметров модели не вызывает качественного изменения ее свойств.
Точность математической модели — ее свойство, отражающее степень совпадения предсказанных с ее помощью значений параметров объекта с истинными значениями этих параметров. Точность модели тесно связана с понятием количественной адекватности.
Истинные значения параметров объекта обычно отождествляют с экспериментами, полученными на модели (в том числе в результате вычислительного эксперимента). Однако погрешности эксперимента во многих случаях оказываются соизмеримыми с погрешностями математической модели.
Пусть объект характеризуется n выходными параметрами У = (У1 , У2 , …Уi ,…Уn ). Пусть Уiм и Уiр - найденное при помощи матмодели и реальное значения i-го выходного параметра. Точность оценивается относительной погрешностью ε = Уi м - Уi р / Уi р , i =  1, n.
1, n.
Уточнение модели состоит в том, что в базовый (грубый) вариант модели, добавляются детали, пока модель не достигнет желаемого качества (необходимой точности).
Универсальность – полнота отображения свойств реального объекта, возможность использования модели для группы однотипных объектов и режимов их функционирования.
Увеличение универсальности (расширение группы объектов, для которых может использоваться модель) значительно усложняют модель.
Требования адекватности, универсальности противоречат друг другу. Поскольку качество любого объекта проявляется во множестве взаимосвязанных между собой свойств, адекватная модель должна отображать как можно больше свойств.
Стремление во всех случаях обеспечить максимальное внешнее правдоподобие может привести к существенным упрощениям, необходимым для реализации модели. И, наоборот, могут быть разработаны модели, в которых при небольшом внешнем правдоподобии используются весьма точные математические методы.
Равнозначимость внешнего и внутреннего правдоподобия
Внешнее правдоподобие - свойства, которые влияют на результаты решения именно этой задачи. Излишние подробности, не влияющие или слабо влияющие на результаты, должны быть исключены (бритва Оккама): они могут усложнить решение задачи и тем самым ухудшить точность решения. В то же время, не должны быть искажены отношения между элементами системы.
Внутреннее правдоподобие зависит от принятых вычислительных методов и техники, используемой при реализации модели.
Разумная степень равнозначимости внешнего и внутреннего правдоподобия должна быть выбрана в каждом конкретном случае: нет смысла применять сложные вычислительные методы, если необходимые для расчета исходные данные отсутствуют, или они известны с большими погрешностями. Такую модель необходимо заменить другой, пусть менее точной, но опирающейся на доступную достоверную информацию·.
Между качеством входной информации и внутренним правдоподобием должен быть установлен своеобразный уровень равнозначности - нет смысла применять сложные вычислительные методы, если заданная мера адекватности достигается простыми методами или необходимые для расчета исходные данные отсутствуют (либо они известны с большими погрешностями).
Для каждой модели существует область применимости (границы размыты): набор объектов и свойств, которые описываются моделью адекватно. Другими словами – любой объект можно моделировать большим числом моделей, каждая из которых будет адекватна в своих границах применимости.
Анализ чувствительности модели
При анализе чувствительности определяется изменения в реакции модели на отклонения отдельных параметров модели. Это позволяет сделать вывод об… Анализ чувствительности особенно важен при решении оптимизационных задач -… Решение практической задачи нельзя считать законченным, если найдено оптимальное решение - некоторые исходные…Этот пример показывает, что информации не обязательно должно быть много. Важно, чтобы она была «по существу вопроса», т. е. соответствовала цели, для которой используется.
Пример. В школе учащиеся знакомятся с информационной моделью кровообращения. Предлагаемой в учебнике анатомии информации достаточно для школьника, но мало для тех, кто проводит операции на сосудах.
Разработка содержательной модели
Объекты моделирования описываются с позиции системного подхода. Исходя из цели исследования, устанавливаются совокупность элементов, взаимосвязи между элементами, возможные состояния каждого элемента, существенные характеристики состояний и соотношения между ними. При этом выясняются свойства, состояния, действия и другие характеристики компонентов объектов в любой форме: устно, в виде схем, таблиц. Формируется представление о компонентах объекта, т.е. информационная модель. В таком словесном описании возможны логические противоречия, неопределенности, которые должны быть, в конце концов, устранены на концептуальном этапе постановки задачи.
При разработке содержательной модели в словесной форме приводятся:
- словесное описание объекта моделирования, явления или процесса: сведения о природе и параметрах элементарных явлений исследуемой системы, о виде и степени взаимодействия между ними, о месте и значении каждого явления в общем процессе функционирования системы;
- формулировка цели исследований с помощью модели и требований к модели (что модель должна позволять исследовать для выполнения цели, необходимая точность решения задачи);
- укрупненный состав и структура системы (в соответствии с действиями, обусловленными функционированием системы для выполнения своего назначения), основные свойства компонентов, условия их функционирования, ограничения, причинно-следственные связи между компонентами;
- предварительные исходные данные для разработки модели и исследований (начальные условия и сведения о факторах, определяющих поведение системы).
Построение содержательной (информационной) модели является отправным пунктом разработки модели.
Все входные параметры объектов, упрощение модели определяются в соответствии с целью моделирования. При этом отбрасываются факторы, несущественные с точки зрения того, кто определяет модель.
Разработка концептуальной модели
Концептуальная модель определяет совокупность параметров системы и внешних воздействий, схему решения поставленной в содержательной модели задачи исследований, исходные данные, необходимые для разработки математической модели.
На основе содержательного описания определяется исходное множество характеристик системы. Для выделения существенных характеристик необходим хотя бы приближенный анализ каждой из них. При проведении анализа опираются на постановку задачи и понимание природы исследуемой системы. После исключения несущественных характеристик выделяют управляемые и неуправляемые параметры. Затем определяется система ограничений на значения управляемых параметров. Если ограничения не носят принципиальный характер, то ими пренебрегают.
Необходимость обоснования включения в модель существенных элементов и свойств, а также исключения из модели несущественных элементов и свойств, требует глубоких знаний о самой системе. Это противоречие (включение одних элементов и исключение других) приводит к определенным трудностям, так как выявление влияния исключения того или иного фактора на степень искажения результатов требует создания моделей с учетом и без учета этих факторов.
Для решения этой проблемы выдвигаются соответствующие гипотезы с последующим их анализом на словесном или вычислительном уровне (при разработке для каждой гипотезы соответствующей математической модели).
Ряд параметров являются случайными величинами по своей природе. Для упрощения модели часть из них может представляться детерминированными средними значениями. Это допустимо, если величина имеет небольшой разброс, или, когда цель моделирования достигается при использовании средних значений.
Всю совокупность вариантов данных можно представить случайной величиной с заданным законом распределения вероятностей.
Для случайных параметров выявляется возможность представления их теоретическими законами распределения. Процедура подбора вида закона распределения заключается в следующем.
По совокупности значений параметра строится гистограмма относительных частот – эмпирическая плотность распределения. Гистограмма аппроксимируется плавной кривой, которая сравнивается с кривыми плотности распределения различных теоретических законов распределения. По наилучшему совпадению выбирается один из законов. Далее по эмпирическим значениям вычисляют параметры этого распределения.
Особую сложность представляет сбор данных по случайным параметрам, зависящим от времени, что характерно для внешних воздействий. Пренебрежение фактами нестационарности параметров существенно влияет на адекватность модели.
Строится два типа концептуальной модели: структурная и функциональная (причинно-следственная) модели.
Объект рассматривается как целостная система, которую расчленяют на подсистемы в соответствии функциями системы (строится по блочному принципу). Компоненты системы связываются структурными отношениями, описывающими подчиненность, логическую и временную последовательность решения отдельных задач.
Структурная модель описывает основные компоненты (элементы) системы, связи между ними и потоки (вещества, энергии, информации), идущие по этим связям.
Если структура системы неизвестна, путем анализа данных о функционировании системы строится гипотеза о структуре, на основании которой создается структурная модель.
Основу функциональной модели составляют законы, которым подчиняются явления и процессы в соответствии с выдвинутыми гипотезами. Функциональные модели состоят из соотношений (операторов), связывающих между собой входные, внутренние и выходные параметры как системы в целом, так и ее компонентов. Функциональная модель разрабатывается для изучения действий системы – описывает преобразования объектом входов в выходы.
Модель строится в соответствии с принятыми гипотезами и предложениями.
Описание внешних воздействий
Модель внешних воздействий должна обладать следующими основными свойствами: – совместимостью с моделью системы; – представительностью;Декомпозиция системы
Декомпозиция системы осуществляется исходя из выбранного уровня детализации модели, который определяется тремя факторами: – целями моделирования; – объемом априорной информации о системе;Подготовка исходных данных для математической модели
Если структура системы неизвестна, описание может формироваться с помощью подбора аппроксимирующих соотношений с той или иной полнотой отображающих… При этом единственной информацией, которой располагает исследователь, является… Исходные данные в общем случае могут быть детерминированными или стохастическими, не все параметры являются…Содержание концептуальной модели
Концептуальная модель содержит:
- выделение объекта из внешней среды (объект определяется как система), определение типа системы (отнесение системы к одному из известных классов), описание внешних воздействий;
- анализ взаимодействия системы с внешней средой, выделение существенных факторов внешней среды, оказывающих влияние на систему, основные свойства системы, процессы, протекающие в системе, причинно-следственные отношения в системе или явлении, возможные последствия изменения этих отношений, связи системы, определяющие параметры системы и внешней среды;
- выявление существенных факторов и механизмов, влияющих на поведение системы, условия функционирования системы, формулировка законов, которым подчиняются явления и процессы в соответствии с выдвинутыми гипотезами;
- введение идеализирующих предположений: формулировка совокупности гипотез о функционировании системы, предположения и допущения, диапазоны изменения параметров и факторов;
- структура системы и основных ее компонентов, функции системы и основных компонентов, основные параметры, позволяющие описывать систему и процесс ее функционирования;
- исходные данные для разработки математической модели: структурная схема системы, точность расчетов, основные операторы, параметры и переменные модели, их классификация, условные обозначения.
2.4.2 Разработка математической модели
Законченная концептуальная постановка позволяет сформулировать математическую постановку задачи моделирования процессов в блоках модели.
Разработка математической модели включает этапы: разработка функциональных соотношений, выбор метода решения задачи, проверка и корректировка модели.
Разработка функциональных соотношений
Математическая модель представляет собой совокупность соотношений (например, уравнений, логических условий, операторов), определяющих характеристики процесса функционирования системы в зависимости от структуры системы, алгоритмов поведения, параметров системы, воздействий внешней среды, начальных условий.
Процесс функционирования формализуется в виде системы математических соотношений, характеризующих изучаемый объект (технологический процесс). Эти определяющие соотношения (суть любой математической модели) устанавливает исследователь. Ошибки в выборе определяющих соотношений приводят к количественно (а, возможно, и качественно) неверным результатам моделирования.
Математическое описание составляется на основе материальных и энергетических балансов, ограничений, а также физических законов, определяющих особенности процесса. Ограничения могут быть обусловлены технологическими, техническими или экономическими причинами.
Совокупность математических соотношений, описывающих поведение и свойства объекта моделирования, определяет вид оператора модели. Для обеспечения корректности постановки задачи к системе уравнений добавляются начальные или граничные условия.
Схема моделирующего алгоритма задает логическую структуру модели процесса функционирования системы (упорядоченную во времени последовательность логических операций), порядок действий при моделировании (что и как следует выполнить на очередном шаге моделирования).
В моделях сложных систем одна и та же информация может быть необходимой для разных блоков (модулей), при совместной их работе требуется видоизменение информации при передаче ее от одного блока к другому (т.е. интерфейсная адаптация). В связи с этим при моделировании сложной системы особое внимание уделяется способам хранения информации и организации информационных потоков.
Выбор метода решения задачи
Основные методы решения задач с помощью математической модели: аналитические или численные методы, имитационное моделирование.
Аналитические методы предполагают поиск искомых величин от исходных параметров модели в виде аналитических выражений. Аналитическое выражение (формула) – совокупность действий, которые нужно проделать в определенном порядке над значением аргумента и константами, чтобы получить значение функции.
Математическая модель представляется в виде явных аналитических зависимостей между характеристиками и параметрами системы и внешних воздействий. Процессы функционирования записываются в виде, некоторых функциональных соотношений (алгебраических, и: интегро-дифференциальных, конечно-разностных и т.п.) или логических условий.
Аналитические методы дают возможность выявить основные зависимости и определить направления дальнейших исследований. Во имя этого иногда сознательно идут на умышленное отступление от первоначальной модели, на упрощение и загрубление ее ради получения аналитических зависимостей и возможности решения задачи хоть и приближенного, но качественно отражающего основные закономерности.
Численные методы: математическая модель представляет собой систему уравнений, к которым применяется некоторый численный метод. Переход от функции непрерывного аргумента к функции дискретного аргумента в численных методах приводит к определенной погрешности вычислений.
Логическая структура метода и характер фигурирующей информации обусловлены скорее типом тех уравнений, к которым удалось свести первоначальную математическую модель. Численный метод всегда реализуется в виде вычислительного алгоритма.
Существует огромное разнообразие численных методов: интерполяция, численное дифференцирование, численное интегрирование, решения систем линейных и нелинейных уравнений, задачи Коши и краевых задач для обыкновенных дифференциальных уравнений, интегральных уравнений, уравнений в частных производных и т.д. Это предполагает выбор метода с позиций эффективности, устойчивости, точности решения конкретной задачи (чаще всего определяется установившимися предпочтениями исследователя и его математической культурой – неформализуемо, как и вся вычислительная математика).
При моделировании сложных процессов далеко не всегда можно модель преобразовать в систему уравнений, пригодную для применения численных методов.
Имитационное моделирование – численный метод исследования свойств системы, путем воспроизведения процесса ее функционирования с помощью вычислительного эксперимента с математической моделью системы – свойства системы определяются на основании анализа накопленного статистического материала. При имитационном моделировании динамические процессы системы – оригинала подменяются процессами, имитируемыми в абстрактной модели, но с соблюдением таких же соотношением длительностей и временных последовательностей отдельных операций.
Одно из основных достоинств имитационных моделей — возможность моделирования даже в тех случаях, когда аналитические модели либо отсутствуют, либо (из-за сложности системы) не дают практически удобных результатов. Имитационное моделирование позволяет учесть влияние большого числа случайных и детерминированных факторов, а также сложных зависимостей при вводе в модель соответствующих элементов и операций.
При имитационном математическом моделировании явлений и процессов сохраняется их логическая структура, последовательность чередования событий во времени. Каждый акт воспроизведения течения процесса называется имитационным экспериментом.
Методами имитационного моделирования анализируется функционирование сложных систем, исследования которых практически невозможно другими методами: системы, подверженные случайным возмущениям, различные варианты управления системами, взаимодействие систем.
Проверка и корректировка модели
Проверка модели включает оценку чувствительности модели к изменению исходных данных, адекватности модели (соответствие поведения модели и реальной системы) и достоверности модели (верификация – проверка того, что модель отвечает заданным ей требованиям).
По результатам проверки модели определяется соответствие принятых существенных факторов, гипотез и допущений заданной точности решений. При необходимости модель корректируется.
Анализ чувствительности модели. При анализе чувствительности оценивается влияние принятых исходных данных (для каждого набора существенных факторов, гипотез, допущений) на результат.
Анализ чувствительности модели осуществляется в несколько итераций.
На первом этапе анализируется одна из переменных (изменяется на какое-либо фиксированное значение, например на 10%), значения всех остальных переменных на входе проекта остаются базовыми - оценивается влияние изменения данной переменной на результат. Для оптимизационных задач оценивается влияние данной переменной на критерий эффективности.
Таким же образом осуществляется расчет показателя чувствительности и критерия для каждой переменной.
На последнем этапе на основании коэффициентов чувствительности ранжируются все переменные в порядке убывания.
Если удается определить, какие параметры в наибольшей степени влияют на значение целевой функции, то для повышения точности получаемого решения целесообразно скорректировать модель в направлении увеличения точности решения в зависимости именно от этих параметров, и упростить модели в отношении параметров, слабо влияющих на результат.
Проверка адекватности модели – определяется степень соответствия результатов, полученных по разработанной модели, удовлетворяющей исследователя (заданным точностям расчетов).
В частности, количественная адекватность оценивается для близких к известным частным и экстремальным случаям применения системы. Анализируется совпадение некоторых характерных особенностей модели и объекта (например, наличие экстремальных точек, возрастание или убывание параметров): оценивается совпадение вида функции (убывающая или возрастающая, с одним экстремумом или несколькими).
Вопрос, что является для данной модели существенным (факторы, принятые гипотезы и допущения), а что нет, решается неформально на основе качественного анализа и с помощью количественных вычислений при анализе чувствительности модели.
В результате анализа для каждой модели (факторы, принятые гипотезы и допущения) определяется мера ее адекватности по сравнению наиболее точной моделью, и из всех выбирается наиболее эффективная модель (факторы, принятые гипотезы и допущения) по степени упрощения при заданной точности расчетов.
Контроль модели.
Исходный вариант модели проверяется по следующим основным аспектам:
Все ли существенные параметры включены в модель?
Нет ли в модели несущественных параметров?
Правильно ли отражены функциональные связи между параметрами?
Правильно ли определены ограничения на значения параметров?
Такая предварительная проверка модели позволяет выявить грубые ошибки.
Если по результатам проверки адекватности выявляется недопустимое рассогласование модели и системы, возникает необходимость в корректировке модели.
Можно выделить следующие виды проверок:
проверка моделей компонентов;
проверка модели внешних воздействий (оценка гипотез математическими методами);
проверка концептуальной модели функционирования системы;
проверка математической модели;
проверка программной модели.
Контроль соответствия значений переменных их физическому смыслу: знаки и величины переменных модели не должны противоречить возможным значениям моделируемых физических величин.
Контроль размерностей: сравниваться и складываться могут только величины одинаковой размерности, эта проверка сочетается с контролем использования одной и той же системы единиц для значений всех параметров.
Контроль порядков: выделение основных и уточняющих слагаемых - сравниваются порядки складываемых величин и исключаются малозначимые параметры.
Контроль характера зависимостей между переменными: выявление качественного совпадения вида модельных зависимостей с видом аналогичных зависимостей в реальной системе (направления и скорость изменения выходных параметров модели соответствуют физическому смыслу моделируемой системы).
Контроль экстремальных ситуаций: в подобных ситуациях поведение модели должно совпадать с поведением системы.
Контроль граничных условий: проверка того, что граничные условия наложены, и значения выходных параметров модели удовлетворяют заданным условиям.
Контроль математической замкнутости: проверка того, что выписанная система математических соотношений дает возможность, притом однозначно, решить поставленную математическую задачу. Проверка замкнутости модели: число независимых уравнений должно быть равно числу искомых параметров задачи.
Например, если задача свелась к отысканию п неизвестных из некоторой системы алгебраических или трансцендентных уравнений, то контроль замкнутости состоит в проверке того факта, что число независимых уравнений должно быть п.
Оценка корректности задачи математической постановки задачи (задача, для которой решение существует, оно единственно и непрерывно). Решение считается непрерывным, если малому изменению исходных данных соответствует достаточно малое изменение решения.
Математическая модель является корректной, если для нее осуществлен и получен положительный результат всех контрольных проверок: размерности, порядков, характера зависимостей, экстремальных ситуаций, граничных условий, физического смысла и математической замкнутости.
Для замкнутой и корректно поставленной математической задачи, т.е. задачи, для которой решение существует, оно единственно и непрерывно зависит от исходных данных, число независимых уравнений должно быть равно числу искомых параметров. Решение считается непрерывным, если малому изменению исходных данных соответствует достаточно малое изменение решения.
Математическая модель считается корректной, если для нее осуществлен и получен положительный результат всех контрольных проверок: размерности, порядков, характера зависимостей, экстремальных ситуаций, граничных условий, физического смысла и математической замкнутости.
Контроль устойчивости модели: изменение в определенных пределах параметров модели не вызывает качественного изменения ее свойств. Причинами низкой устойчивости модели могут быть деление на малую по модулю величину, вычитание близких друг к другу приближенных значений величин, введение дополнительных параметров, известных с невысокой точностью.
Корректировка модели.
При корректировке модели могут уточняться существенные параметры, ограничения, показатели исхода операции, связи показателей исхода операции с существенными параметрами. После внесения изменений в модель вновь выполняется оценка чувствительности и адекватности.
Корректировка модели завершается определением и фиксацией области пригодности модели: множество условий, при соблюдении которых точность результатов моделирования находится в допустимых пределах.
Оптимизация модели. Сущность оптимизации моделей состоит в их упрощении при заданном уровне адекватности. Основными показателями, по которым возможна оптимизация модели, выступают время и затраты средств для проведения исследований на ней. В основе оптимизации лежит возможность преобразования моделей из одной формы в другую. Преобразование может выполняться либо с использованием математических методов, либо эвристическим путем.
По результатам корректировки модели делается вывод об адекватности модели заданной цели исследований (верификация модели).
Верификация (доказательство, подтверждение, (лат. verus - истинный и facio - делаю) - подтверждение на основе представления объективных свидетельств того, что установленные требования были выполнены.
Верификация модели состоит в проведении исследования с помощью отладочных и проверочных тестов.
Осуществляется взаимная проверка различными подходами, качественное и количественное исследование моделей, проверка непротиворечивости, сравнение результатов, полученных аналитическими и численными методами, сопоставление с практикой.
Метод асимптотического ряда моделей (Е.С. Вентцель) – спор моделей.
Идея метода основана на аксиоме - при бесконечном повышении качества модели она приближается к самому объекту. Следовательно, построив ряд моделей возрастающей точности, мы сможем на основании модельных экспериментов предсказать, какими будут выходные параметры у реального объекта, который ещё предстоит построить в будущем. Здесь используются прогнозирующие способности моделей.
Для простоты будем считать, что проектируемый объект характеризуется одним выходным параметром yp, значение которого и предстоит спрогнозировать.
Для проектируемого объекта строится ряд моделей возрастающей точности: М1, М2, … Мn,... Все они моделируют один и тот же объект, но делают это с возрастающей степенью точности - чем старше модель, тем выше её качество. Испытания моделей (вычислительные эксперименты) дают ряд значений модельного параметра - ym1, ym2, … ymn, … .
 Этот ряд значений ym1, ym2, … ymn, … будет асимптотически приближаться к реальному значению yp, которое спрогнозировать (определить на графике его величину). После чего можно вычислить точность каждой из построенного ряда моделей.
Этот ряд значений ym1, ym2, … ymn, … будет асимптотически приближаться к реальному значению yp, которое спрогнозировать (определить на графике его величину). После чего можно вычислить точность каждой из построенного ряда моделей.
"Спор" этих моделей заключается в выборе рабочей модели - последняя построенная модель самая точная, но одновременно она и самая сложная, а значит, и самая неэкономичная.
Рабочей моделью должна быть самая простая модель, которая ещё обеспечивает требуемую точность модельных экспериментов eдоп .
Для контроля правильности полученной системы математических соотношений требуется проведение ряда обязательных проверок.
Реализация математической модели в виде программ для ЭВМ
Для моделирования процесса функционирования системы на ЭВМ математическая модель процесса и соответствующий моделирующий алгоритм преобразуется в реализующую их программу – информационная знаковая модель преобразовывается в компьютерную модель.
Компьютерная модель - математическая модель, выраженная средствами программной среды (компьютерная программа).
Процесс разработки надежного и эффективного программного обеспечения требует применения современных технологий программирования (структурной, абстрактной, объектно-ориентированной, визуальной), развитой библиотеки совместимых программных модулей.
Процесс создания программного обеспечения можно разбить на следующие этапы:
-составление технического задания на разработку пакета программ программного обеспечения;
-проектирование структуры программного комплекса;
-кодирование алгоритма;
-тестирование и отладка;
-эксплуатация и сопровождение.
Техническое задание на разработку программного обеспечения
ТЗ на разработку программного обеспечения в общем виде может включать разделы:
1. Определение решаемой задачи, название программного комплекса, система программирования для его реализации и требования к аппаратному обеспечению.
2. Описание математической модели, метод обработки входных данных для задач не вычислительного характера (обработки данных).
3. Управление режимами работы программы –основные требования к способу взаимодействия с программой (интерфейс «пользователь-компьютер»).
4. Входные данные, пределы, в которых они могут изменяться, значения, которые они не могут принимать, и т.д.
5. Выходные данные, сведения об их точности и объеме, способах хранения и т.д.
6. Возможные ошибки пользователя при работе с программой (например, ошибки при вводе данных), способы диагностики (т.е. выявление ошибок), способы защиты от этих ошибок, а также реакция пользователя при совершении им ошибочных действий и реакция ПО (компьютера) на эти действия.
7. Тестовые задачи, на которых в простейших случаях проводится отладка и тестирование программного обеспечения.
Порядок программной реализации с использованием конкретного математического обеспечения отображается схемой программы.
Схема программы представляет собой интерпретацию логической схемы моделирующего алгоритма разработчиком программы на базе конкретного языка. Различие между этими схемами заключается в том, что логическая схема отражает логическую структуру модели процесса функционирования системы, а схема программы – логику компьютерной реализации модели с использованием конкретных программно-технических средств моделирования.
Для начертания перечисленных схем используется набор символов, определяемых ГОСТ «Единая система программной документации. Схемы алгоритмов и программ. Обозначения условные графические».
Обычно схема является наиболее удобной формой представления структуры моделирующих алгоритмов. Однако используются и другие формы, например, граф-схемы, операторные схемы.
2.4.3 Практическое использование построенной модели и анализ результатов моделирования
Конечная цель моделирования - принятие решения, которое должно быть выработано на основе всестороннего анализа полученных результатов. Этот этап решающий - либо вы продолжаете исследования, либо заканчиваете.
Полученные выводы часто способствуют проведению дополнительной серии экспериментов, а иногда и к изменению модели.
Независимо от области применения созданной модели необходимо проводить качественный и количественный анализ результатов моделирования.
Всесторонний анализ результатов моделирования позволяет:
- обозначить область применения модели;
- проверить обоснованность гипотез, принятых на этапе математической постановки, оценить возможность упрощения модели при сохранении требуемой точности;
- показать, в каком направлении следует развивать модель в дальнейшем.
Результаты моделирования используются для принятия решения о работоспособности системы, для выбора лучшего проектного варианта или для оптимизации системы.
3 МАТЕМАТИЧЕСКИЕ МОДЕЛИ СТРУКТУРЫ И СОСТОЯНИЯ СИСТЕМЫ
3.1 Модель структуры системы
Основные понятия структуры системы
В сложной системе объединены различные по своей физической и технической природе компоненты, методы их исследования различны.
Система изучается по частям, затем на основании свойств подсистем и связей между ними формируется вывод об общих свойствах системы в целом (решение задачи анализа – синтеза исследования системы).
Разбиение системы на модули способствует более эффективной организации анализа и синтеза систем, так как оказывается возможным, абстрагируясь от второстепенных деталей, уяснить суть основных соотношений, существующих в системе и определяющих исходы системы.
Формально любая совокупность элементов данной системы может рассматриваться как ее подсистема.
Обычно подсистемы являются некоторыми самостоятельно функционирующими частями системы. Например, в производственном комплексе предприятия можно выделить подсистемы, соответствующие отдельным цехам или технологическим линиям.
Правильное выделение подсистем сложной системы способствует упрощению расчетов при моделировании и более наглядной интерпретации его результатов. Модель подсистемы составляется в виде структуры из моделей элементов и целиком входит в полную модель управляемой системы. Поскольку подсистема — это самая крупная, функционирующая отдельно от общих связей, структурная единица, важным этапом работы является ее декомпозиция, основанная на сборе фактов, выявлении и оценке различных воздействующих факторов.
Понятие структуры системы связано с понятием целостности системы. Основа целостности (принцип целостности) в системном представлении, ее несводимости к простой сумме частей, состоит в связях, которые объединяют составные части в единую систему с присущими ей новыми свойствами.
Разным типам связей соответствуют различные типы целостности.
Связям созидания (кристалл, сооружение) соответствует структурный тип целостности, функциональным связям (функционирование искусственных систем, жизнедеятельность организмов) соответствует функциональный тип целостности, связям развития (сложная техническая система, растение, эмбрион) – генетический тип целостности.
Целостность выступает как обобщенная характеристика системы, которой присуще сложное внутреннее строение (сложная техническая система, общество), как единство компонентов во всем многообразии связей. Философская категория «часть – целое» стало основой формирования понятий элемент, структура, система.
Понятие связи – основа понимания упорядоченности объектов.
Общество - не механическое объединение индивидуумов, а организованная упорядоченная система, в рамках которой формируется индивидуум с его потребностями, особенностями, целями (Маркс).
Понятие целостности стало основой системного подхода – исследование объекта как составной части целого. Отсюда возникла необходимость выделения объектов из целого в процессе исследований.
Существование (функционирование, развитие) любой системы (биологической, социальной, экономической, технической) определяется ее структурой, обеспечивающей динамическую взаимосвязь отдельных частей системы.
Как нет общепринятого определения понятия сложной системы, так и нет строгого определения понятия структуры системы.
Тем не менее, сложившиеся представления о структуре исходят из общесистемных понятий (наличие элементов, существование связей между ними) и предполагают конфигурацию системы, не зависящую от времени.
Отсюда одно из определений системы – не свободно выбранное, а упорядоченное множество взаимосвязанных элементов, имеющих собственную структуру и организацию.
Элемент – неделимый в контексте конкретной системы и конкретных ее исследований компонент. Элемент связан с другими в сложном взаимодействии.
Понятия структуры системы, связи с внешней средой формулируются на основе целей, назначения системы, целей и задач исследований системы (формулируемых исследователем).
Структурные и функциональные свойства системы тесно связаны между собой – совокупность элементов и связей определяется исходя из распределения функций между элементами системы.
Структура системы — это совокупность устойчивых связей объекта, обеспечивающих его целостность - сохранение основных свойств при различных внешних и внутренних изменениях.
С другой стороны, структура системы — частичное упорядочение элементов системы и отношений между ними по какому-либо признаку.
Отличие в функционировании (поведении) различных элементов и необходимость согласования их функционирования в рамках системы приводят к формированию стойких внутренних связей между элементами – к формированию структуры.
Сама система, все взаимодействия и связи между ее подсистемами и элементами подчинены специфическим для данной системы законам, которые определяют особенности ее существования и развития. Между подсистемами данной системы могут быть различные отношения, связи и взаимодействия, которые составляют структуру системы.
Для описания системы рассматриваются три основные уровня моделей:
- внутреннее строение системы неизвестно – модель "черного ящика" (система представлена только своими входами и выходами, исследуется зависимость выходов от входов);
- состав системы (описание составляющих систему компонентов);
- структурная схема системы (описание всех элементов и связей системы между элементами и с внешней средой).
Структурные и функциональные свойства системы тесно связаны между собой – систему можно представить как целое, совокупность элементов и связей определяется исходя из распределения функций и целей между элементами системы.
Модель состава и структуры системы
Модель состава – список элементов системы. Сложность построения модели состава состоит в ее неоднозначности. Это же относится и к границам системы –… Модель состава ограничивается снизу тем, что считается неделимым элементом,… Для разных целей исследования модель состава системы может быть разной (примеры: состав самолета с различных точек…Виды структур
При моделировании систем вообще и, в частности, для целей структурного анализа используются различные модели, отображающие: • функции, которые система должна выполнять; • процессы, обеспечивающие выполнение указанных функций;Пример разработки моделей деятельности организации
Этапы разработки:
• выделение множества объектов, оказывающих существенное влияние на деятельность структурного элемента;
• спецификация входных и выходных потоков (информации, материалов, продуктов, услуг, финансов и т.д.);
• выявление основных процессов, определяющих деятельность структурного элемента и обеспечивающих реализацию его целевых функций;
• спецификация потоков между основными процессами деятельности, уточнение связей между процессами и внешними объектами;
• оценка объемов, интенсивности и других необходимых характеристик потоков;
• разработка функциональной модели деятельности структурного элемента;
• объединение моделей структурных элементов в единую модель деятельности организации.
Цель организации — стремление к максимальному результату, выражаемому в максимизации ценности капитала, при постоянном сохранении определенного уровня ликвидности и достижении целей производства и сбыта с учетом социальных задач. Вспомогательной стоимостной целью является стремление к оптимальной расчетной прибыли за период.
При анализе производственно-экономической системы решаются следующие задачи.
Анализ организационной структуры:
- описание состава организации и построение её структурной схемы;
- определение функций отдельных подразделений, раскрытие их структурной схемы;
- описание материальных, вещественных и информационных связей;
- построение обобщённой структурной информационной модели предприятия.
Анализ функциональной структуры:
- изучаются функции управления в структурных подразделениях существующей системы;
- выбирается состав автоматизированных функций;
- определяются их взаимосвязи;
- составляется обобщённая функциональная структура задач управления АСУП.
Анализ технической структуры:
- определяются основные элементы, участвующие в основных информационных процессах (регистрации и подготовки информации, сборе и передаче, хранении и обработке, воспроизведении и выдаче информации);
- составляется формальная структурная модель системы технических средств с учётом топологии расположения элементов и энергетического взаимодействия их как между собой, так и с внешней средой.
3.2 Модель состояния системы
Состояние системы и ее функционирование
Состояние системы характеризуется перечнем всех ее свойств и текущими (обычно динамическими) значениями каждого из этих свойств. Перечень свойств системы является, как правило, статическим, поскольку эти свойства составляют неизменяемую ее основу.
Свойства, которые характеризуют объект и его поведение, остаются неизменными. Объект может только менять состояние.
Например, лифт характеризуется теми неизменными свойствами, что он может двигаться вверх и вниз, оставаясь в пределах шахты. Любая модель должна учитывать эти свойства лифта, так как они входят в его определение.
Любое происшествие, которое может быть причиной изменения состояния системы, называется событием. Изменение состояний называется переходом.
Состояние системы - это набор параметров системы, определяющий характер ее функционирования и значение выходной величины на определенном временном интервале.
Если хоть одна характеристика системы изменится, это будет новое состояние. Модель конкретного состояния объекта ("моментальная фотография") – статическая модель.
Процесс - набор состояний системы, соответствующий упорядоченному изменению (непрерывному или дискретному) некоторого параметра, определяющего характеристики (свойства) системы - параметра процесса.
Пусть выбран некоторый физический параметр (чаще всего время) такой, что различные состояния соответствуют разным его значениям. Набор состояний - это еще не процесс.
Пример: робот-манипулятор. Серия фотографий в разных точках пространства, сделанных наугад или перемешанных – это набор состояний, но еще не процесс. Последовательные во времени движения – процесс.
Функционирование - процессы, которые происходят в системе, стабильно реализующей фиксированную цель.
Функционирование системы проявляется в ее переходе из одного состояния в другое или в сохранении какого-либо состояния в течение определенного периода времени.
Кроме основных функциональных свойств компонента, необходимых для выполнения системой целевых задач, компонент может привносить с собой в систему некоторые нежелательные свойства.
В реальном мире все без исключения объекты изменяются во времени. В природе любой объект стремится перейти в некоторое равновесное состояние (принцип устойчивости) как с окружающей средой, так и между отдельными элементами самого объекта. Нарушение этого равновесия приводит к изменениям различных параметров объекта и его переходу в новое равновесное состояние.
Пример параметров этого процесса: изменение во времени линейных, угловых координат, температуры, давления.
Для обоснования принятия решения о наилучшем способе достижения системой заданной цели функционирования необходимо на моделях исследовать различные ситуации, которые могут возникнуть при функционировании системы. Для изучения действий системы разрабатывается модель функционирования (функциональная модель), которая позволит прогнозировать процесс функционирования по заданным начальному состоянию системы и параметрам процесса.
При построении модели функционирования исходя из содержательной постановки задачи определяются:
- основные действия системы, необходимые для выполнения цели (цель действия, описание действия, способ выполнения действия);
- основные компоненты системы, соответствующие действиям;
- основные условия функционирования - интервал времени функционирования, множества входных и выходных воздействий и области их изменения, множества характеристик состояния системы и области их возможных изменений.
В функциональной модели отражены происходящие в системе процессы (физические, химические, механические, информационные и др.), связи параметров системы с внешней средой - описываются свойства системы и ее поведение в пространстве и во времени под влиянием тех или иных воздействий. С помощью нее определяются оптимальные режимы функционирования системы и ее элементов в различных условиях внешней среды и оптимальная организация взаимодействия элементов.
Состояние системы может быть представлено набором из n параметров, каждому состоянию системы соответствует точка в n-мерном пространстве состояний системы, функционирование системы проявляется в перемещении этой точки по некоторой траектории в пространстве состояний (задается начальным состоянием).
Состояние системы может быть описано ее обобщенными координатами (совокупность параметров, достаточная для определения положения системы) и обобщенными скоростями (производные параметров системы по параметру процесса - времени). Трехмерное представление пространства состояний (фазового пространства) приводится на рисунке.
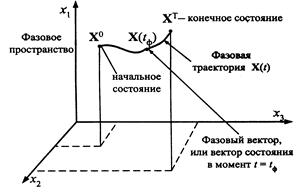 Состояние системы изображается в виде точки с этими координатами в некотором условном фазовом пространстве. По осям пространства могут лежать любые параметры системы – в общем случае фазовое пространство многомерно.
Состояние системы изображается в виде точки с этими координатами в некотором условном фазовом пространстве. По осям пространства могут лежать любые параметры системы – в общем случае фазовое пространство многомерно.
Фазовые координаты системы - набор численных значений параметров состояния системы.
Для символьной записи процесса изменения состояния системы введем многомерную (по числу исследуемых характеристик) величину z, описывающую их конкретные значения. Все множество возможных величин – Z, z∈Z.
Введем параметр процесса t, множество его значений T, t∈T.
Опишем z как функцию этого параметра z = z (t).
Координаты z1, z2, . . . , zn – координаты состояния (фазовые координаты). Z (t) – вектор переменных состояния.
Z(tф) – вектор состояния (фазовый вектор) в фиксированный момент t = tф.
Модель содержит: описание множества возможных состояний и описание закона, в соответствии с которым система переходит из одного состояния в другое.
Тогда процесс Stot есть некоторое правило перехода от ситуации со значением параметра to к ситуации со значением t > t0 через все его промежуточные (непрерывные или дискретные) значения:
Stot (z (to)) = z (t), z∈Z, t∈T.
Каждому элементу t множества Т ставится в соответствие вполне определенный элемент z другого множества Z, т.е. в виде отображения z (t) или
T → Z: z (t) ∈Z, t∈T.
Функционирование системы во времени рассматривается как процесс перехода ее из состояния в состояние: состояние системы изменяется как функция времени z (t), называемая фазовой траекторией.
Функции z (t) (или их вероятностные характеристики) могут зависеть от ряда параметров рm, m = 1, 2, . . . , m*, р ∈ Р.
В общем случае функции z (t) представляют собой реализации случайных функций Z (t) с совокупностью многомерных законов распределения L[Z (t)].
Состояние системы может определяться набором действительных чисел. Например, положение самолета в данный момент времени можно описать вектором фазовых координат (z1, z2, z3), где z1 – наклонная дальность, z2 - азимут, z3 - угол места.
В начальный момент времени t0 состояния z имеют значения, равные z0 (в общем случае задаются законом распределения L0[Z (t0)]).
В любой момент времени состояние объекта определяет набор свойств (обычно статический) объекта и текущие (обычно динамические) значения этих свойств. Под "свойствами" подразумевается совокупность всех связей и элементов объекта.
Статическая модель "черного ящика" - свойства системы не изменяются во времени.
При построении статической модели отображаются свойства системы, не зависящие от времени (модели "черного ящика" и структуры системы).
Следующий шаг состоит в том, чтобы конкретнее отобразить происходящие изменения во времени: различаются части, этапы происходящего процесса, рассматриваются их взаимосвязи. Например, динамический вариант "черного ящика" – описание изменения состояния "ящика" во времени (от начального до конечного состояния).
В процессе функционирования может изменяться модель состава: включаются новые элементы в некоторой последовательности действий.
Пример: сетевой график производства – графы сетевой структуры. Вершины графа – выполняемые производственные операции, ребра указывают, какие операции не могут начаться, пока не выполнятся предыдущие. Длительности операций задаются длинами или весами ребер, что позволяет находить на графе "критические пути", т.е. последовательность операций, от которых зависит ритмичность всей работы.
В динамической модели "черного ящика" задаются процессы на входах и выходах. Рассматривая выход у (t) системы (это может быть вектор) как ее реакцию на управляемые u(t) и неуправляемые ν(t) входы x (t) = {u(t), ν(t)}, можно модель "черного ящика" выразить как совокупность двух процессов: X T = { x (t)} и Y T = { у (t)}, t ∈T.
Если считать у (t) результатом некоторого преобразования Ф процесса x(t) в "черном ящике", т.е. у (t) = Ф (x(t)), то модель "черного ящика" предполагает, что это преобразование неизвестно.
Формализация процесса функционирования системы
Формализация процесса функционирования системы основана на следующих положениях:
- любая система функционирует во времени, взаимодействуя с внешней средой, и в каждый момент времени может находиться в одном из возможных состояний;
- в данный момент времени состояние системы определяется предыдущими состояниями и входами системы, выходные параметры определяются состояниями и входами, относящимися к данному и предшествующим состояниям системы.
Основные составляющие модели: модели отдельных элементов (подсистем) системы, внешние параметры (воздействия окружающей среды или управлений), внутренние параметры (состояние и процессы в моделируемой системе, которые определяют выходные параметры), функциональные соотношения между внешними и внутренними параметрами модели (оператор модели). В динамической модели все составляющие модели имеют временной характер.
Параметры могут быть постоянными или переменными, управляемыми или неуправляемыми. На переменные параметры устанавливаются ограничения - пределы их изменения.
Математическая модель системы - это задание множества входов, состояний, выходов и связей между ними (отображений):
 .
.
Здесь:
Х – входы в систему, x Î X;
Z – состояние системы z (t) = α (t), z ∈Z;
Y – выходы системы у (t) = β (t, z (t)), t ∈ T;
α – отображение (функция, правило перехода), определяющее зависимость состояния системы от входных воздействий;
β – отображение (функция, правило перехода), определяющее зависимость выходных воздействий от состояния системы.
Конкретизируя множества X, Z и Y и отображения α и β, можно перейти к моделям различных систем.
В обобщенном виде модель характеризуется следующими воздействиями, параметрами и правилами:
x - набор входных воздействий в системе и вся их допустимая совокупность X, x Î X;
у - набор выходных воздействий в системе и вся их допустимая совокупность У , у Î У;
р - набор постоянных параметров, характеризующих свойства системы и влияющих на выходные воздействия, и вся их допустимая совокупность Р, р Î Р;
z - набор изменяющихся параметров (параметров состояния), характеризующих свойства системы, влияющих на выходные воздействия, и вся их допустимая совокупность Z, z Î Z;
t - параметры процесса в системе и вся их допустимая совокупность T, t Î T;
α - правило (функция, оператор) определения параметров состояния z системы по входам х, постоянным параметрам р, параметру процесса t.
β - правило (функция, оператор) определения выходных характеристик у системы по входам х, постоянным параметрам р, параметру процесса t и параметрам состояния z.
Параметры состояния системы находятся по правилу α из уравнения состояния:
z = α (х, р, t).
Выходные характеристики системы находятся по правилу β из уравнения выхода:
у = β (x, p, t, z).
Входной процесс Х T - множество значений х (t) входных воздействий, определенных для всех t Î T за весь период функционирования: Х T {х (t): t Î T}.
Фрагмент входного процесса - отрезок входного процесса, ограниченный моментами времени t0 и t1. Любой входной процесс может быть расчленен на совокупность фрагментов (наоборот – объединение фрагментов - не всегда является входным процессом).
Выходной процесс – выходное воздействие у (t1) на внешнюю среду или другие элементы: УT {у (t): t ∈ T}.
Для всех моментов времени, для которых заданы входные и выходные процессы, определено состояние системы.
Модель функционирования в общем случае для произвольного начального момента времени t ÎT и интервала t0t1
z (t1) = α (t0t1,р, z (t0), Хt0t1); у (t1) = β (t0t1,р, z (t0), Хt0t1).
Уравнения состояния и уравнения выхода позволяют описать процесс функционирования системы траекториями ZТ и УТ, каждая точка которых характеризует для некоторого момента времени t ∈T состояние системы z (t). Конкретный вид обеих траекторий определяется входным процессом ХТ, начальным состоянием z (t0) и операторами α и β.
На основе введения приведенных воздействий, параметров и правил модель может быть записана как кортеж
∑ : {x, у, p, t, z, α, β}, x Î X, у Î У, p Î P, t Î T, z Î Z.
Разбор конкретной модели по такой формализованной схеме состоит в отнесении различных величин, объектов, понятий к составляющим кортежа (составление списков существенных входов, выходов, процессов, параметров), что является эффективным средством понимания функционального содержания системы, составления и корректировки ее модели, выявления важнейших сторон моделирования.
Примеры формальной записи моделей.
Автомобильный двигатель:
- входы (внешние воздействия): своевременная подача в камеру сгорания газовой смеси определенного состава;
- выход: мощность двигателя;
- неизменяемые параметры системы: объем камеры сгорания. Число и расположение цилиндров, степень сжатия, размеры и массы частей силового механизма (поршней, коленвала, маховика);
- параметр процесса: время или угол поворота коленвала;
- параметры состояния: температура и давление в камере сгорания, скорости движущихся частей, силы трения в двигателе;
- правило α (уравнение состояния): термодинамические уравнения, описывающие процесс сгорания газовой смеси, и механические уравнения, описывающие движение частей силового механизма;
- правило β: запись мощности двигателя в виде функции от скоростей движения частей силового механизма.
Информационная система обработки текста:
- входы: объем текста, численная оценка его сложности;
- выход: длительность обработки текста;
- неизменные параметры: скорость чтения текста. Число повторных чтений в зависимости от сложности;
- изменяющиеся во времени параметры: объем проделанной работы:
- параметр процесса: стадия работы или время;
- правило α: зависимость объема проделанной работы от объема и сложности текста, параметров распознающей системы, времени;
- правило β: зависимость длительности обработки от объема проделанной работы.
Все составляющие кортежа не обязательны: их может быть больше (системы с управлением) или меньше («черный ящик»).
Другими составляющими кортежа могут быть входные случайные воздействия (выделяется отдельно часть входов х), характеристики структуры системы в отличие от характеристик элементов (выделяются отдельно из параметров р), некоторые свободные параметры модели, все множество значений которых должно быть учтено при расчете выходов (операции взятия максимума), управления в целенаправленных системах.
Часто даже при незначительных изменениях постановки задачи может происходить переход величин из одной составляющей кортежа в другую. Например, при некоторых условиях мало меняющуюся величину, сделав ее условно постоянной, отнести к неизменным параметрам р, или наоборот, отнести ее к параметрам состояния. Путем математической замены переменной меняют местами параметр процесса и один из параметров состояния.
Модель может задаваться в виде описания или в виде количественных воздействий.
В модели "черного ящика" присутствует минимальное число элементов, описывающих модель - только входы и выходы, т.е. связи системы со средой, и отсутствуют сведения о внутреннем содержании системы и о границах между системой и средой ("стенки ящика").
Если это преобразование известно (модель "белого ящика"), то его можно описать тем или иным способом (в зависимости от того, что известно о содержании системы и о ее свойствах): инерционность или безинерционность, непрерывность, гладкость, монотонность, симметричность, наличие шумов, помех или искажений на входе и выходе, зависимость от предыстории движения – выход определяется не только значением входа в данный момент, но и теми значениями, которые были на входе в предыдущие моменты, и т.д. В самой системе с течением времени как под влиянием входных воздействий, так и независимо от них могут происходить изменения, что также нужно отразить в модели.
Понятие входных переменных может быть уточнено.
● X может быть не одной переменной, а вектором переменных {X1, X2, …, Xn}, так как сложные системы, которые мы моделируем, обычно связаны со средой множеством факторов {X1, X2, …, Xn}.
● Логически удобно разделить вектор X на входные переменные (собственно X) и переменные управления U. Такие факторы принято называть управляемыми переменными или просто управлением. Обычно значения переменных U чем-то ограничены: Umin ≤ U ≤ Umax.
● P — мало меняющиеся переменные, которые в этом случае называют параметрами системы; по своей сути они мало отличаются от X. В прикладных задачах их часто выносят отдельно, так как динамически они (на отрезке времени рассмотрения или существования задачи) не меняются и не меняют свойств системы.
● Помехи Q. Управление U — фактор, который призван компенсировать негативное действие помех Q на выходной показатель цели Y.
3.3 Модель процесса функционирования
Функционирование системы заключается в выполнении технологических процессов преобразования вещества, энергии или информации.
В сложных системах, как правило, одновременно протекает несколько процессов. Каждый процесс состоит из определенной последовательности отдельных элементарных операций. В системах с программным управлением, обеспечивающих параллельное выполнение нескольких процессов, имеются алгоритмы управления совокупностью параллельно функционирующих процессов.
Процесс функционирования системы можно рассматривать как последовательную смену ее состояний Z=Z(z1(t), z2(t), …, zn(t)) в n–мерном пространстве. При заданном начальном состоянии системы  можно определить ее состояние в любой момент
можно определить ее состояние в любой момент 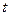 из интервала
из интервала 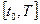 , если известны операторы переходов и выходов.
, если известны операторы переходов и выходов.
Задачей моделирования процесса функционирования исследуемой системы является построение функций Z, на основе которых можно провести вычисление интересующих характеристик процесса функционирования системы. Для этого должны иметься соотношения, связывающие функции Z с переменными, параметрами и временем, а также начальные условия Z0=Z(z1(t0), z2(t0), …, zn(t0)) в момент времени t = t0.
При построении математических моделей процесс функционирования системы может быть представлены как непрерывно-детерминированный (например, дифференциальные уравнения, уравнения состояния); дискретно-детерминированный (конечные автоматы); непрерывно-стохастический (системы массового обслуживания); обобщенный или универсальный (агрегативные системы).
Для определенных классов систем разработаны формализованные схемы и математические методы, которые позволяют описать функционирование системы, а в некоторых случаях – выполнить аналитические исследования.
Установление функциональных зависимостей
Исходным материалом для построения математической модели процесса функционирования системы является его содержательное описание. На основании исходного описания в математической модели процесса… Для моделирования процесса функционирования системы на ЭВМ математическая модель процесса преобразовывается в…Функционально – физический анализ технических объектов.
Технический объект разделяется на элементы, каждый из которых имеет вполне определенную функцию по обеспечению работы объекта или его элементов. Элементарная физическая операция может быть реализована с помощью одного физико-технического эффекта. Предельное разделение объекта возможно до неделимых элементов с минимальным числом функций. Среди всех элементов особое внимание уделяется главным элементам (обозначается Е0). Элементы объекта обозначаются Е0,Е1, ... ЕN.
Цель функционально-физического анализа - определение, на основе каких физико-технических эффектов работает каждый элемент, анализ функций и физических операций (преобразований) и как элементы функционально связаны между собой.
Конструктивная функциональная структура представляет собой ориентированный граф, вершинами которого являются наименования элементов, ребрами — функции элементов.
Функционально – физический анализ направлен на изучение:
- функций каждого элемента технического объекта и функциональных связей элементов между собой;
- физических операций (преобразования) каждого элемента технического объекта и как элементы функционально связаны между собой;
- физико-технических эффектов, законов, зависимостей на основе которых работает каждый элемент технического объекта и как они взаимосвязаны между собой.
Построение конструктивной функциональной структуры является первым этапом функционально – физического анализа Любой технический объект можно разделить на несколько элементов каждый из которых имеет вполне определенную функцию по обеспечению работы объекта или его элементов. Предельное разделение возможно до неделимых элементов с минимальным числом функции.
Конструктивная функциональная структура представляет собой ориентированный граф, вершинами которого являются наименования элементов объекта, а ребрами — функции элементов.
Аналогично анализу функций технического объекта может быть проведен анализ технологических процессов. При этом для технологических процессов функциональная структура представляет собой граф вершинами которого являются обрабатываемые объекты, а ребрами элементарные операции с указанием режимов обработки.
Технология или процесс - способ, метод или программа преобразования вещества, энергии или информации из заданного начального состояния в заданное конечное состояние с помощью определенных технических объектов.
При этом выделяются подсистемы, реализующие технологическую функцию (превращение исходного материала в конечный продукт), энергетическую функцию (превращение вещества или извне полученную энергии в конечный вид энергии, необходимый для реализации технологической функции, функцию управления (управляющие воздействия на подсистемы в соответствии с заданной программой функционирования).
В зависимости от задач исследования системы в понятие структуры включаются различные аспекты функционирования системы.
Анализ функционирования системы и анализ ее структуры - две взаимосвязанные стадии исследования (поскольку связаны между собой структурные и функциональные свойства системы): зная законы функционирования отдельных элементов, но не зная структуры системы, нельзя представить систему как целое и понять, как она функционирует.
Структурно-функциональная модель описывает элементы, связи и присущие им функции.
Элементы (или подсистемы) связаны структурными соотношениями (могут быть представлены в виде схем, карт, диаграмм), которым соответствуют функции.
Помимо функциональных модулей, в структурную схему могут включаться логические блоки, позволяющие изменять характер функционирования в зависимости от того, выполняются или нет некоторые заранее заданные условия.
Структурно-функциональные модели – статические модели – они, не описывают процесс функционирования системы (зависимость изменения свойств системы от времени, начальных и граничных условий).
Функциональные, геометрические и функционально-геометрические модели отражают соответственно только функциональные, только пространственные и одновременно функциональные и пространственные свойства оригинала.
Модель строится в виде логической структурной схемы системы по модульному принципу - в виде совокупности стандартных блоков-модулей. При этом можно строить и совершенствовать модель итерационным методом, добавляя к основной схеме блок за блоком. Каждая модель может быть разделена на блоки, а блоки — на подблоки. Этот процесс деления блоков на подблоки продолжается до необходимого уровня детализации описания системы. Таким образом, модель функционально подразделяется на подмодели.
Функционально стоимостной анализ.
Функциональные, геометрические и функционально-геометрические модели отражают соответственно только функциональные, только пространственные и… Функционально стоимостной анализ (ФСА) функций объекта (технологического… Содержание работ при проведении ФСАПути уменьшения неопределенностей
Одним из путей снятия неопределенностей объектов, на которые направлены действия систем, действий реального противника или партнера является выбор… Неопределенность может быть учтена при равнозначимом анализе, который… - определение частных производных критерия эффективности по неопределенным параметрам,Пример. Реле как дискретная система.
Реле – это элемент, входная и выходная величины которого могут принимать лишь конечное число значений (как правило, два или три).
Электромагнитное реле - типичный релейный элемент, исполнительные органы (контакты) которого могут находиться только в двух устойчивых состояниях – в замкнутом и разомкнутом.
 Реле состоит из сердечника с обмоткой, якоря, контактов и входного выключателя; кроме того, имеются входные клеммы х и выходные клеммы у. Если входной выключатель разомкнут – обмотка обесточена, контакты разомкнуты; если замкнут – в обмотке появляется ток. Когда ток достигает определенной величины, сердечник притягивает якорь, контакты замыкаются, на выходных клеммах появляется напряжение.
Реле состоит из сердечника с обмоткой, якоря, контактов и входного выключателя; кроме того, имеются входные клеммы х и выходные клеммы у. Если входной выключатель разомкнут – обмотка обесточена, контакты разомкнуты; если замкнут – в обмотке появляется ток. Когда ток достигает определенной величины, сердечник притягивает якорь, контакты замыкаются, на выходных клеммах появляется напряжение.
Электромагнитные реле используются в так называемых контактных схемах. Основным явлением здесь оказывается сам факт замыкания или размыкания соответствующих контактов, наличие или отсутствие напряжения на выходе схемы в зависимости от напряжения на входе.
Обычная формализация процессов такого рода сводится к интерпретации наличия напряжения на входе (сигнал х = 1) или на выходе (сигнал у = 1) как истинных высказываний, а отсутствие напряжения на входе (сигнал х = 0) или на выходе (сигнал у = 0) – как ложных высказываний, а также зависимости у = f(x) как некоторой функции исчисления высказываний. Таким образом, реле здесь выступает в качестве логического элемента.
Устройства релейного действия применяются для изменения состояния во многих областях техники – в пневматических, гидравлических, электрических цепях и т.д. Реле выполняют функции защиты, контроля, управления, сигнализации. Реле времени создает необходимую задержку в передаче воздействий между отдельными узлами автоматики.
В соответствии с физической природой внешних явлений, вызывающих действие реле, их делят на электрические (ток, напряжение, мощность, сопротивление, частота), механические (перемещение, скорость, давление, уровень), тепловые, акустические, химические, магнитные и т.д.
Релейные элементы характеризуются порогом срабатывания и порогом отпускания. Порог срабатывания - минимальное абсолютное значение возрастающего воздействия, при котором элемент изменяет свое состояние и одновременно изменяет воздействие на выходе в соответствии с релейной характеристикой (преобразование непрерывной входной величины в дискретное значение выходной величины). Порог отпускания – минимальное абсолютное значение уменьшающегося выходного воздействия, при котором релейный элемент возвращается в первоначальное состояние. Релейный элемент с фиксацией – элемент остается в занятом состоянии и после снятия воздействия на входе, возвращение в первоначальное состояние – после подачи воздействия на другой вход элемента (или другого знака на тот же вход). Другие характеристики релейного элемента – быстродействие, время срабатывания, время отпускания.
Детерминированные и неопределенные модели
Закономерности, описывающие процессы и явления объективного мира, можно условно разделить на две группы: однозначно определенные (детерминированные) и находящиеся в условиях неопределенности.
В зависимости от способа задания параметров, исходной информации, начальных условий и способа нахождения характеристик системы, математические модели можно подразделить на два больших класса: детерминированные и неопределенные (вероятностные, стохастические).
В детерминированных моделях все исходные данные, ограничения и целевая функция (т.е. некоторое соотношение, количественно характеризующее поставленную перед системой цель) задаются в виде конкретных чисел, векторов или числовых функций.
В детерминированных моделях используются различные классические методы математики: дифференциальные, линейные, разностные и интегральные уравнения, операторы для сведения к алгебраическим моделям и др. При совместном рассмотрении этих соотношений состояния системы в заданный момент времени однозначно определяются через параметры системы, входную информацию и начальные условия.
По степени математической абстракции детерминированные модели можно разделить на сложные и упрощенные.
Сложные модели описывают все причинные связи какой-то реальной системы и позволяют точно прогнозировать поведение системы в зависимости от изменения переменных (или параметров).
Упрощенные модели описывают только существенные зависимости (идеализированные модели).
Между этими двумя моделями существует ряд моделей, отличающихся степенью детализации. На практике чаще всего применяются упрощенные модели с разной степенью детализации. При этом считается, что имеются существенные и несущественные факторы: существенные учитываются, несущественные отбрасываются. Между принятыми в модели факторами и результирующими показателями устанавливается жесткая детерминированная связь. Широкое распространение идеализированных моделей вызвано их простотой и возможностью логического обоснования.
Детерминированные системы – системы, процессы в которых взаимосвязаны так, можно проследить цепь причин и следствий.
К детерминированным относятся те закономерности, которые по заданным с определенной точностью характеристикам входных воздействий позволяют установить вполне определенный (детерминированный) отклик (реакцию) выходных воздействий исследуемого объекта.
В статическом режиме детерминированные системы описываются алгебраическими уравнениями, в динамическом режиме – дифференциальными уравнениями.
Модель детерминированная, если каждому входному набору параметров соответствует вполне определенный и однозначно определяемый набор выходных параметров; в противном случае модель недетерминированная, стохастическая (вероятностная).
Приведенные выше физические модели — детерминированные. Если в модели S(p) = g(p)t2/2, 0 < t < 100 мы учли бы случайный параметр — порыв ветра с силой р при падении тела, например, так: S = gt2/2, 0 < t < 100, то мы получили бы стохастическую модель (уже не свободного) падения.
При решении одних задач случайные составляющие практически не влияют на результат и в модели не учитываются. В других задачах решение может быть получено только при учете случайных составляющих или различных неопределенностей, и соответствующие математические методы закладываются в модель.
Достаточность детерминированной модели или необходимость учета неопределенностей иногда очевидна, иногда переход к модели, учитывающей неопределенность, происходит вследствие неудовлетворенности результатами, полученными на детерминированной модели.
В неопределенной модели неопределенные закономерности описывают случайные события (могут протекать по- разному при одних и тех же условиях). Неопределенные закономерности (параметры, связи) должны быть выявлены уже на концептуальной стадии создания модели.
Неопределенность понимается в том смысле, что соответствующие характеристики системы находятся в условиях приближения и неполноты информации. В «чистом виде» неопределенных процессов нет - описание неопределенности может быть разным в зависимости от количества и качества имеющейся информации (имеется не вся необходимая информация, элементы могут быть описаны по аналогам, что не всегда соответствует целям исследований). Характеристики системы зависят от большого количества различных факторов (некоторые из них могут быть вообще неизвестны), выбор для моделирования существенных факторов, влияющие на систему, может иметь неоднозначный характер (как объективный, так и субъективный).
Во многих моделях исследователь имеет дело с неточными исходными данными, неопределенность которых порождается различными факторами.
Например:
- результаты измерения – шумы, ошибки измерения, ошибки округления;
- прогнозные данные – незнание, неопределенность, неполнота информации;
- методические ошибки, ошибки дискретизации;
- экспертные оценки – субъективность данных.
Неопределенность может возникнуть на этапе содержательной модели (лингвистическая неопределенность – неоднозначность определений, смысла фраз, нечеткость описания явления или процесса) и на этапе концептуальной модели (неопределенность принятых гипотез и предположений).
В зависимости от типа неопределенности – методы описания неопределенных данных, включая вероятностную, нечеткую и интервальную модели, - каждая из них имеет свои методы анализа и область применения.
Математически неопределенность может быть описана стохастически, статистически, с позиций нечетких множеств.
Стохастическое описание используется тогда, когда неопределенные параметры носят вероятностный (случайный) характер. При этом необходимо, чтобы был определен закон распределения таких случайных параметров.
В стохастической системе состояние и выход – случайные величины, операторы перехода и выхода не определяют конкретные значения состояния и выхода, как в детерминированном случае, а лишь устанавливают вероятности их реализации.
Статистическое описание является частным случаем стохастического – заданы только выборочные оценки каких-либо характеристик случайной величины или наборы некоторых случайных параметров.
Нечеткая модель основана на понятии нечеткого множества (нечеткая переменная и ее функция принадлежности, задающая степень принадлежности конкретного значения величины х некоторому множеству s).
При описании с позиций нечетких множеств неопределенный параметр задается некоторым множеством возможных его значений, определяющих степень принадлежности объекту (например, при выделении элементов из внешней среды). Нечеткое множество описывает систему с нечеткими, размытыми границами. Обычно функция принадлежности задается экспертным путем на основе информации об источниках неопределенности переменной х.
Интервальная модель – неопределенность параметра х описывается его возможными значениями в виде [x] = [xmin; xmax]. Внутри интервала не задается никакой вероятностной меры – все значения внутр интервала предполагаются равновозможными (не путать с равновероятными).
Любому реальному процессу присущи случайные флюктуации (отклонения от средних значений). Однако выбор детерминированной или вероятностной математической модели зависит от того, учитываются ли случайные факторы. Выделение детерминированных моделей в отдельный класс объясняется широким их применением и разнообразием математических методов решения детерминированных задач.
Если хотя бы один параметр модели или ограничительная функция имеет в качестве своих значений случайный вектор или случайную величину, то это случайная (стохастическая) модель. В этом случае под однозначностью определения характеристик моделируемого процесса понимается однозначное определение распределений вероятностей для характеристик процесса при заданных распределениях вероятностей для начальных условий и возмущений.
Стохастический характер модели связан с наличием в объекте и среде различных неконтролируемых, но существенных факторов, которые можно моделировать статистически. Состояние системы в этом случае Y=F(X, U, E(t)), где E(t) – случайный процесс, моделирующий имеющуюся неопределенность объекта и среды. Эта неопределенность может быть связана как с быстрым изменением параметров объекта, так и с помехами, накладывающимися на измеряемые значения сигналов на входе и выходе объекта.
Стохастический объект и его модель ведут себя неоднозначно в одинаковых ситуациях, что моделируется случайным вектором E(t), статистические свойства которого должны быть заданы. В простейшем случае Y=F(X, U)+E(t).
Примером стохастического объекта является любой биологический организм, который в одинаковых условиях ведет себя по-разному. В этом случае Y описывает поведение объекта, которое строго зависит от внешних условий, а все отклонения от этого регулярного поведения образуют «случайную помеху» E(i).
Переход от детерминированной модели к стохастической осуществляется таким образом, чтобы она отражала в себе случайный характер данных и самой модели. Способ перехода выбирается в зависимости от сведений об изучаемой модели: уверенности в правильности и надежности данных и модели. При этом возможно, что эти сведения ошибочны.
В общем случае для стохастических объектов оператор является случайным (например коэффициенты линейного дифференциального уравнения, весовые функции и т.д.).
В зависимости от учета в модели случайностей при работе и управлении объектом моделирования непрерывности или дискретности процесса рассматривают дискретно-детерминированные, дискретно-детерминированные, непрервно-детерминированные, дискретно-стохастические, непрерывно-стохастические модели.
Основной схемой формализованного описания систем, для которых характерны непрерывный характер изменения времени и наличие случайностей в поведении, служит аппарат систем массового обслуживания. Именно для таких систем характерны стохастический характер функционирования (случайное появление заявок на обслуживание), завершение обслуживания в случайные моменты времени, наличие входного и выходного потока заявок, наличие приборов обслуживания, поток событий. Время рассматривается как непрерывный процесс, имеются случайности, сама система представляет собой систему массового обслуживания.
Статические и динамические модели
Существенным признаком классификации моделей является их возможность описывать изменения параметров объекта во времени.
Статичный или динамичный характер системы (что отображается в модели) определяется в зависимости от целей моделирования. При построении модели основным является сравнение времени существенных изменений внешних воздействий и соответствующих характерных временных переходов объекта в новое равновесное состояние с окружающей средой и между элементами внутри системы.
В статической модели можно выделить важнейшие свойства и параметры (или сочетания), определяющие качество системы, не зависящие от времени (надежность, стоимость, долговечность и др.). В статической модели объект сохраняет состояние равновесия: параметры остаются постоянными при постоянных внешних воздействиях.
Модель называется статической, если среди параметров, участвующих в описании модели, нет временного параметра. Статическая модель в каждый момент времени дает лишь «фотографию» системы, ее срез.
Закон Ньютона F = ma — это статическая модель движущейся с ускорением а материальной точки массой т. Эта модель не учитывает изменение ускорения от одной точки к другой.
При таком подходе можно ставить оптимизационные задачи по критерию, выраженному этой функцией. В случае линейной целевой функции, линейных неравенств, линейной математической модели задачи технико-экономического содержания (например, распределение ресурсов) решаются как задачи линейного программирования.
Если изменения параметров во времени происходят столь медленно, что ними можно пренебречь, то такую модель называют квазистатической.
Модель динамическая, если среди параметров модели есть временной параметр, т. е. она отображает систему (процессы в системе) во времени.
В динамической модели от времени зависят независимые переменные (параметр процесса), неизвестные функции (фазовые переменные), характеризующие состояние системы (перемещения, скорости, ускорения элементов системы, силы и моменты, давление и расход жидкости в трубопроводе, напряжение и сила тока в электрической сети и др.).
Модель S = gtz/2 — динамическая модель пути при свободном падении тела. Динамическая модель типа закона Ньютона: F(t) = a(t)m(t). Еще лучшей формой динамической модели Ньютона является: F(t) = s"(t)m(t).
Динамические системы могут быть с дискретными состояниями (множество состояний конечно или счетно) или с непрерывным множеством состояний.
Системы с дискретными состояниями характеризуются тем, что в любой момент времени можно однозначно определить, в каком именно состоянии находится система. Для такой идентификации обязательно нужно знать тот признак, который отличает одно состояние системы от другого. Например, при исследовании систем массового обслуживания в качестве такого признака обычно используют число заявок в системе. Соответственно, изменение числа заявок в системе интерпретируется как переход системы в новое состояние.
Смена состояний может происходить либо в фиксированные моменты времени, множество которых дискретно (например, поступление новых заявок на обслуживание), либо непрерывно (изменение температуры тела при нагревании). В соответствии с этим различают системы с дискретным временем переходов (смены состояний) и системы с непрерывным временем переходов (точнее, «живущие» в непрерывном времени).
В детерминированных системах новое состояние зависит только от времени и текущего состояния системы. Если имеются условия, определяющие переход системы в новое состояние, то для детерминированной системы можно однозначно указать, в какое именно состояние она перейдет.
Для стохастической системы можно указать лишь множество возможных состояний перехода и, в некоторых случаях, - вероятностные характеристики перехода в каждое из этих состояний.
Основная форма динамической математической модели - дифференциальные уравнения.
Стационарные и нестационарные модели.
Стационарные системы – такие системы, свойства которых не изменяются во времени.
Реакция стационарной системы на любой заданный тип возмущения зависит только от интервала времени между моментом начала действия входного возмущения и данным моментом времени, т.е. свойство стационарности означает, что процесс преобразования входных сигналов инвариантен относительно сдвига, как от текущего времени, так и от момента приложения входного сигнала. Реакция нестационарной системы зависит как от текущего времени, так и от момента приложения входного сигнала. В этом случае при сдвиге входного сигнала во времени (без изменения его формы) выходные сигналы не только сдвигаются во времени, но и изменяют свою форму.
Примеры стационарных моделей.
При ламинарном течении жидкости (скорость течения невелика) в длинной трубе постоянного сечения на достаточно большом удалении от входа частицы жидкости движутся параллельно оси трубы, и профиль скоростей частиц в сечении остается с течением времени неизменным – параметры модели не зависят от времени.
Термодинамическое равновесие обшивки самолета при полете в плотных слоях атмосферы. Обшивка, получая тепловую энергию от воздушного потока, одновременно излучает ее в окружающее пространство, в соответствии с законом Стефана-Больцмана тем больше, чем выше ее температура (εТ = σ Т4, εТ – интегральная излучательная способность – энергия излучения с единицы поверхности в единицу времени, σ – постоянная).
В общем случае состояние системы z (t) и выход системы y (t) являются функциями не только z (t0), и Хt0t, но и самого интервала t0t:
z (t) = α (t0t, z (t0), Хt0t); у (t) = β (t0t, z (t0), Хt0t).
При одних и тех же значениях z (t0), и Хt0t, перемещая по оси времени интервал t0t, можно получить различные значения z (t) и y (t).
Введем в рассмотрение оператор сдвига Ñt, применение которого к произвольной величине приводит к ее сдвигу вдоль оси времени на интервал t.
Система называется стационарной, если для операторов перехода и выхода выполняются условия:
z (Ñtt) = α (Ñt t0t, Ñt z (t0), Ñt Хt0t) = Ñt z (t);
у (Ñtt) = β (Ñt t0t, Ñt z (t0), Ñt Хt0t) = Ñt у (t).
На рисунке 3.1 представлено второе из условий, согласно которому должно выполняться равенство у (Ñtt) = Ñt у (t).
Для стационарной системы модель функционирования можно записать в виде, независимом от t0t:
 z (t) = α (z (t0), Хt0t); у (t) = β (z (t0), Хt0t).
z (t) = α (z (t0), Хt0t); у (t) = β (z (t0), Хt0t).
Стационарные модели применяются для описания различных потоков (жидкости, газа, тепла) в случае постоянства условий на входе и выходе потока.
В нестационарной модели время – одно из существенных переменных. Например, движение жидкости в трубе при изменении параметров на входе (изменение скорости при истечении жидкости из сосуда).
Стационарные математические модели описывают системы, в которых протекают так называемые установившиеся процессы – процессы, в которых интересующие нас параметры постоянны во времени.
К установившимся (стационарным) относят и периодические процессы, в которых некоторые выходные параметры остаются неизменными.
Например, математическая модель маятника является стационарной по отношению к независящим от времени периоду и полуразмаху колебаний, хотя материальная точка перемещается во времени относительно положения равновесия.
Частным случаем стационарных моделей являются модели статические, которые включают описание связей между основными переменными процесса в установившихся режимах (в равновесном состоянии без изменения во времени).
Например, математическое описание статики химико-технологического процесса состоит обычно из трех видов уравнений: материального и теплового балансов, термодинамического равновесия системы (характеристика движущей силы) и скоростей протекания процессов (химических реакций, тепло- и массопередачи и т.п.).
Для расчетов медленных процессов или процессов, протекающих с небольшими отклонениями от стабильных условий, принимается допущение, позволяющее считать процесс установившимся.
Подобное допущение принимается, например, для расчета теплового баланса турбины при половинной, трехчетвертной или полной нагрузке или для решения методами линейного программирования задачи смешения материалов.
Стационарные математические модели (кроме статических) обычно состоят из дифференциальных уравнений, статические – из уравнений алгебраических.
Формализация системы в виде автомата
Состояние объекта характеризуется перечнем (обычно статическим) всех свойств данного объекта и текущими (обычно динамическими) значениями каждого из… Наличие внутреннего состояния объектов означает, что порядок выполнения… Система представляется в виде автомата, перерабатывающего дискретно поступающую информацию, и меняющего свое…Формализация системы в виде агрегата
Для анализа и синтеза структуры сложной системы с разнородными элементами (детерминированными, стохастическими, непрерывными, дискретными)… Унифицированной математической моделью разнородных элементов системы является… Понятие агрегата определяется на основании единого подхода к формализации процесса функционирования системы:Моделирование процесса функционирования агрегата
Цель моделирования функционирования – получение характеристик, определяемых состоянием моделируемой системы. Для этого необходимо фиксировать в… Применительно к агрегату это означает, что необходимо получать значения… В основе построения моделирующего алгоритма лежат моменты поступления входных и управляющих сигналов: моделирование…Моделирование агрегативных систем
В А-системе не могут быть элементы-неагрегаты. Пример возможной схемы агрегативной системы приведен на рисунке 4.2. А-система состоит из агрегатов А1, А2, . . . Функционирование А-системы связано с переработкой информации.Модель сопряжения элементов
В модели сопряжения элементов отражается не процесс функционирования элементов, а только такие их свойства, которые существенны для сопряжения… Основные предположения, концентрирующие интуитивные представления о… 1. Взаимодействие между системой и внешней средой, а также между агрегатами внутри системы осуществляется посредством…Основные фундаментальные законы механики
Законы Ньютона.
Материальная точка - тело, размеры и форма которого несущественны в рассматриваемой задаче. Пример идеализации исходя из целей и задач. Материальная точка не имеет размеров. Тогда что такое линия? Определение линии, плоскости: «Существует хотя бы одна…Fij = - Fji.
Fij - сила, действующая на i–ю точку со стороны j–ой точки.
Тяготение между телами осуществляется через гравитационное поле (поле тяготения), которое является одной из форм материи.
Здесь масса материальной точки характеризует гравитационные свойства этой точки и называется гравитационной массой (массой тяжести).
Для всех тел отношение их инертных и гравитационных масс постоянно. Инертные и гравитационные массы равны и связаны с силой тяжести тела соотношением m = F/g.
Векторная характеристика гравитационного поля – его напряженность g, которая равна отношению силы тяготения, действующей на материальную точку, к его массе: g = F/m.
Закон всемирного тяготения: между любыми двумя материальными точками действуют силы взаимного притяжения
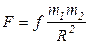 ,где f - гравитационная постоянная (сила взаимного притяжения между двумя точками одинаковой массы на расстоянии единицы длины).
,где f - гравитационная постоянная (сила взаимного притяжения между двумя точками одинаковой массы на расстоянии единицы длины).
Свойство притягивать тела обусловлено массой тела. Гравитационная сила – сила, с которой два тела притягиваются друг к другу (сила тяготения).
Каждое тело создает вокруг себя силовое поле – поле тяготения. Напряженность этого поля в любой его точке характеризует силу, которая действует на другое тело, находящееся в этой точке: g = F/m.
Закон сохранения массы – масса изолированной системы тел (или материальных точек) не изменяется при любых происходящих в ней процессах.
Масса тела – физическая величина, которая является мерой его инерционных и гравитационных свойств.
Масса – величина аддитивная, т.е. масса m любой системы материальных точек (например, твердого тела) равна сумме масс mi всех n точек системы: m = 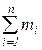 .
.
Центром инерции или центром масс системы материальных точек называется точка С (хс, ус, zc), радиус-вектор rc которой связан с массами mi и радиус-векторами rc всех n точек соотношением
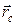 =
= 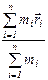
Пример: хранение делящегося вещества.
1. Формулировка содержательной модели.
Объект моделирования: имеется некоторое количество радиоактивного вещества (область I), окруженного толстым слоем защитного материала (область II).
 Формулировка цели исследований и задачи моделирования: разработать математическую модель, которая позволит определить закономерности изменения масс радиоактивного вещества и защиты.
Формулировка цели исследований и задачи моделирования: разработать математическую модель, которая позволит определить закономерности изменения масс радиоактивного вещества и защиты.
Исходные данные: массы МI(0), МII(0) и размеры LI(0), LII(0) радиоактивного вещества и защитного материала, длина свободного пробега продуктов распада в радиоактивном материале λI и защите λII, μI - атомный вес радиоактивного вещества.
2. Формулировка концептуальной модели.
Формулировка закона, которому подчиняется явление: все, что вылетает из области радиоактивного вещества (области I) поглощается в области защиты (области II), и суммарная масса обоих веществ со временем не меняется – модель строится на основании закона сохранения материи.
Выделение существенных факторов и формулировка гипотез.
Все продукты распада, не испытывая столкновений с атомами вещества, покидают область I: длина свободного пробега продуктов распада λI значительно больше характерных размеров самого материала LI, т.е. λI >> LI, продукты деления полностью поглощаются в защите (области II). Это гарантируется при выполнении противоположного условия λII << LII , где λII - длина пробега продуктов распада во втором веществе, LII - его характерный размер.
3. Разработка математической модели.
В любой момент времени справедлив баланс
MI (0) + MII (0) = MI (t) + MII (t). (1)
Введение дополнительных гипотез.
Для определения текущих значений двух масс (замыкания математической формулировки задачи) необходимо привлечь дополнительное соображение о характере распада: число атомов радиоактивного вещества, распадающихся в единицу времени (скорость распада), пропорционально общему числу атомов вещества(чем больше самого вещества, тем больше продуктов распада).
Применим еще раз закон сохранения вещества к отрезку времени dt. За небольшое время dt между моментами t и t + dt всего распадется атомов
NI (t + dt) – NI (t) = - αNI (t + ξdt), α>0, 0<ξ<1.
В этом уравнении, описывающем баланс атомов, в правой части стоит знак минус (вещество убывает), а величина NI (t + ξdt) отвечает некоторому среднему значению числа атомов за рассматриваемое время, α – коэффициент пропорциональности.
Это же уравнение в дифференциальной форме:
dNI (t) / dt = - αNI (t).
Учитывая, что MI (t) = μI NI (t), где μI – атомный вес вещества I, получаем
dMI (t) / dt = - α MI (t). (2)
Уравнения (1) и (2) вместе с условиями λI >> LI и λII << LII , а также величинами α, MI (0), MII (0) и составляют математическую модель рассматриваемого объекта.
Коэффициент пропорциональности (чем больше самого вещества, тем больше продуктов распада) определяется конкретным веществом.
4. Исследования модели и решение задачи.
Интегрируя (2) получаем, что масса делящегося вещества убывает по экспоненциальному закону
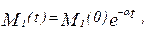
и при t → ∞ в области I вещество полностью исчезает.
Так как суммарная масса в соответствии с (1) остается постоянной, то в области II, количество вещества растет:

и при t → ∞ продукты распада полностью переходят из области I в область II.
Закон Архимеда – на погруженное в жидкость тело действует выталкивающая сила, равная весу жидкости, вытесненной телом:
F = gVρ0.
Сила приложена в центре тяжести объема погруженной части тела.
Закон сохранения импульса.
К = Полный импульс (количество движения) замкнутой системы (на которую не…Работа, энергия, мощность
Если сила перемещает тело на некоторое расстояние, то она совершает над телом работу. Работа = Сила х Перемещение. При F = const (в случае постоянной силы в процессе перемещения) A = F s, в случае переменной силы – интеграл от силы…Работа против силы тяжести.
Чтобы поднять тело (увеличить расстояние от центра Земли), над ним следует совершить работу. Работа, совершаемая силой F при движении против силы… Это не полная потенциальная энергия – только приращение энергии при подъеме… Wп = m.Работа, затрачиваемая на ускорение.
Если ускорение сообщается телу, находящемуся в состоянии покоя, совершаемая над телом работа запасается в виде кинетической энергии Wк = mv2/2. Кинетическая энергия тела К = mv2/2 – в случае поступательного движения тела… В случае вращения под действием момента силы закрепленное на оси твердое тело приобретает угловое ускорение.Работа против сил трения.
Сила трения направлена вдоль поверхности соприкосновения в сторону, противоположную движению Fтр = μFн, где μ – коэффициент трения, Fн –… μ = tgα (при каком угле наклона тело начинает двигаться). Сила трения равна скатывающей силе Fтр = Fс.Динамика поступательного движения.
В прямоугольных декартовых координатах уравнение движения имеет вид: dKx/dt = Fх, dKy/dt = Fy, dKz/dt = Fz. mi= Fiх, mi= Fiу, mi = Fiz. m dVx/dt = Fх, m dVy/dt = FyТело, брошено под углом к горизонту.
В двумерной постановке тело, брошенное под углом к горизонту, рассматривается как материальная точка, движущаяся под действием лишь одной силы -…Движение тела переменной массы.
(mv) = F + v1 , где F – главный вектор всех сил, действующих на тело, v1 – скорость присоединяющейся массы до присоединения (если dm/dt > 0) или… Ускорение w тела переменной массы w = 1/m(F + Fp), где Fp = (v1 – v)dm/dt =… Пример. Движение ракеты в условиях отсутствия внешнего силового воздействия.Модель колебательного процесса
Колебания по своей физической природе весьма разнообразны (механические, электромагнитные колебания и др.). Осциллятор - система, в которой какие-либо параметры совершают колебания при… При колебаниях происходит знакопеременное отклонение параметров от их определенных значений. Эти значения могут…Модель консервативной системы.
Механическая энергия консервативной системы (отсутствие рассеяния энергии) сохраняется неизменной в процессе движения системы: имеет место закон… Простейший пример консервативной системы: тело совершает горизонтальные… Если х обозначает смещение тела массой m из состояния равновесия, а сила, с которой пружины действуют на тело…Электрическая подсистема.
Типовыми простейшими элементами электрической подсистемы являются резистор с электрическим сопротивлением R, конденсатор без потерь заряда с… При описании их функционирования используются переменные: сила тока I,…Модели элементов гидравлических систем
Участок трубопровода. По аналогии с электрическими системами: разности электрических потенциалов… Постоянный расход идеальной жидкости. Для участка достаточно длинного трубопровода с круглым поперечным сечением…Модели элементов пневматических систем
Газ называют совершенным, если для него справедливо уравнение Клайперона-Менделеева p = rRT, где T – температура газа, R - удельная газовая… В пневматической системе, как и в гидравлической, величиной, имеющей смысл… При установившемся ламинарном течении по трубопроводу вязкого газа с постоянным расходом m' = ∆р V/RT или…Транспортная задача.
Транспортные модели описывают перемещение (перевозку) какого-либо товара из пункта отправления (исходный пункт, например место производства) в пункт назначения (склад, магазин, грузохранилище). Назначение транспортной задачи — определить объем перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок. При этом должны учитываться ограничения, налагаемые на объемы грузов, имеющихся в пунктах отправления (предложения), и ограничения, учитывающие потребность грузов в пунктах назначения (спрос). В транспортной модели предполагается, что стоимость перевозки по какому-либо маршруту прямо пропорциональна объему груза, перевозимого по этому маршруту. От того, насколько рационально будет прикрепление пунктов потребления к пунктам производства, зависит объем транспортной работы.
В качестве критерия оптимальности можно принять минимальную стоимость перевозок всего груза (общие транспортные расходы), либо минимальное время его доставки. Рассмотрим задачу с первым критерием.
Возникает задача о наиболее рациональном прикреплении потребителей к поставщикам, при котором удовлетворяются их потребности, а суммарные затраты на перевозку минимальны. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.
Параметры задачи.
Имеется m пунктов производства А1, …, Аm однородного продукта и n пунктов потребления В1,…, В n.
Предложение поставщика в каждом i-м пункте составляет аi единиц, i = 1, . . ., m.
Спрос потребителя в каждого j-ом пункте составляет bj единиц, j = 1, . . .. n.
Транспортные расходы на перевозку единицы продукции из Аi в Вj составляет cij (себестоимость, расстояние, тариф, время, расход топлива).
Требуется определить оптимальный план перевозок, при котором суммарные транспортные расходы минимальны продукции (управляющий параметр - количество продукции, перевозимой от каждого поставщика к каждому потребителю).
Обозначим xij – количество продукции, перевозимой от i-го поставщика j-му потребителю
i = 1, . . ., m, j = 1, . . .. n.
Математическая модель задачи
Суммарные затраты на транспортировку из всех пунктов производства во все пункты потребления:
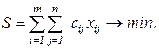 тр
тр
Управляющий параметр: xij ≥ 0 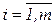 ,
, 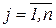 - количество единиц продукции, поставляемой из Аi в Вj – перевозки из пунктов потребления в пункты производства исключены.
- количество единиц продукции, поставляемой из Аi в Вj – перевозки из пунктов потребления в пункты производства исключены.
Ограничения
Суммарное предложение должно быть не меньше суммарного спроса
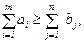
В каждый пункт потребления доставляется продукции не менее необходимой
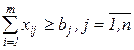 ,
,
От каждого поставщика вывозится продукции не более имеющейся
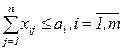 .
.
Всякое неотрицательное решение систем уравнений называется опорным планом (совокупность чисел xij , 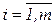 ,
, 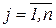 , удовлетворяющая приведенным ограничениям). Решение X*=(xij ), при котором функция S принимает минимальное значение - называется оптимальным планом транспортной задачи.
, удовлетворяющая приведенным ограничениям). Решение X*=(xij ), при котором функция S принимает минимальное значение - называется оптимальным планом транспортной задачи.
Это общая задача линейного программирования – ограничения в виде неравенств (несбалансированная транспортная модель).
Модель, в которой ограничения имеют вид равенств, называется сбалансированной транспортной моделью.
Несбалансированная модель может быть приведена к сбалансированной – неравенства заменены равенствами (в общем случае путем введения фиктивных неотрицательных переменных – фиктивного поставщика или потребителя продукции).
Замкнутая транспортная модель предполагает ограничения в виде равенств:
- сумма спроса равна сумме предложений;
- спрос каждого пункта потребления удовлетворяется полностью;
- весь продукт из каждого пункта производства должен быть вывезен.
Особая структура замкнутой транспортной задачи (все ограничения имеют вид равенств) позволяют решать ее простыми методами.
На пересечении i-ой строки и j-го столбца стоит тариф с и сюда же заносится значение хij – количество продукции, поставляемой от i-го поставщика j-му потребителю.
При большой размерности задачи (m x n) отыскание оптимального плана путем непосредственного перебора становится трудоемкой. Решение транспортной задачи состоит из двух этапов: нахождение начального плана, улучшение его и получение оптимального плана перевозок.
К рассмотренной транспортной задаче приводятся различные практические задачи, никак не связанные с планированием перевозок, но которые могут быть сформулированы в терминах транспортной задачи.
Для решения транспортной задачи составляется транспортная таблица.
| Номер поставщика | Номер потребителя | Предло-жение | |||||
| . . . | j | . . . | n | ||||
| c11 x11 | c12 x12 | . . . | c1j x1j | . . . | c1n x1n | a1 | |
| c21 x21 | c22 x22 | . . . | c2j x2j | . . . | c2n x2n | a2 | |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| i | ci1 xi1 | ci2 xi2 | . . . | cij xij | . . . | cin xin | ai |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| m | cm1 xm1 | cm2 xm2 | . . . | cmj xmj | . . . | cmn xmn | am |
| Спрос | b1 | b2 | . . . | bj | . . . | bn |
В общем случае транспортную модель можно применять для описания ситуаций, связанных с управлением запасами, управлением движением капиталов, составлением расписаний, назначением персонала и др.
Хотя транспортная задача может быть решена как обычная задача линейного программирования, ее специальная структура позволяет разработать алгоритм с упрощенными вычислениями(на основе симплекс-метода).
Задача коммивояжера.
Пример простой комбинаторной задачи – задача о назначениях. Здесь требование целочисленности выполняется автоматически, поскольку задача о назначениях представляет собой частный случай транспортной задачи (в котором m = n, ai = bj = 1). Более общий случай представляет собой задача коммивояжера.
Имеется n+1 городов; задана матрица С =  расстояний между этими городами. Выезжая из исходного города (с номером 0), коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город 0. В каком порядке объезжать следует города, чтобы суммарное расстояние было минимальным?
расстояний между этими городами. Выезжая из исходного города (с номером 0), коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город 0. В каком порядке объезжать следует города, чтобы суммарное расстояние было минимальным?
Это напоминает задачу о назначениях (минимизация суммарного расстояния), но уже не по всем матрицам перестановок, что усложняет решение.
Параметры задачи
xij = 1, если коммивояжер из города i переезжает в город j,
xij = 0 в противном случае,
где i, j = 0, 1, 2, . . ., n.
Задача минимизации
 (суммарное расстояние минимальное)
(суммарное расстояние минимальное)
при условиях
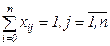 (коммивояжер выезжает из каждого города, кроме начального, один раз)
(коммивояжер выезжает из каждого города, кроме начального, один раз)
 (коммивояжер въезжает в каждый город, кроме начального, один раз)
(коммивояжер въезжает в каждый город, кроме начального, один раз)
ui – uj + nхij ≤ n - 1, 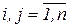 , i ≠ j.
, i ≠ j.
Здесь переменные ui принимают целые неотрицательные значения. Последнее условие вводится для того, чтобы путь коммивояжера не распался на несколько не связанных между собой подциклов (задача о назначениях) – любой путь состоит из одного цикла.
Задача о ранце.
Имеется n предметов, вес предмета j – aj, его ценность – сj. Требуется загрузить ранец набором предметов с общим весом А с максимальной суммарной ценностью.
Введем переменные xj,  , имеющие следующий смысл
, имеющие следующий смысл
xj = 1, если j-й предмет подлежит загрузке,
xj = 0 в противном случае.
Задача о ранце сводится к максимизации
с1х1 + с2х2 + . . . . + сnxn → max
при условиях
xj = 1, 
xj = 0
а1х1 + а2х2 + . . . . + аnxn ≤ А.
Пример.
Оптимальная загрузка бомбардировщиков различных типов бомбовым запасом с целью максимизации суммарного эффекта данной системы боевых операций.
Обозначим через i = 1, 2, . . ., m типы бомб, через j = 1, 2, . . ., n – типы бомбардировщиков, через к = 1, 2, . . ., р – боевые операции.
Введем величины
bi- имеющийся запас бомб типа i,
aik- эффективность бомбы типа i на операции к,
nj- планируемое число вылетов бомбардировщика j,
wk- "вес", приписываемый командованием операции к.
Искомой величиной здесь является
xijk- количество бомб типа I, подлежащее загрузке в бомбардировщик j при его использовании в операции к.
Задача сводится к минимизации суммарного эффекта
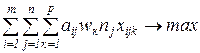
при ограничениях
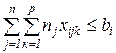 , i = 1, 2,. . ., m
, i = 1, 2,. . ., m
xijk ≥ 0, xijk – целые числа.
Общая задача теории расписаний.
Обычно это задача календарного планирования, и ее варианты являются схемами основных задач по организации производства.
Имеется n станков и m деталей, каждая из которых должна пройти обработку на всех станках в определенной последовательности. Задано аij – время, необходимое для обработки j-ой детали на i-ом станке. Требуется найти такой порядок обработки деталей, который минимизировал бы общее время выполнения всех работ (длину производственного цикла). Несмотря на большое прикладное значение, пока получено решение только для случая двух станков. В этом случае, поскольку операции на первом станке можно выполнить без задержек, оптимизация заключается в минимизации суммарного времени простоя второго станка.
Примеры сведения практических задач к канонической транспортной задаче
Многие практические задачи, связанные с планированием перевозок, не укладываются в рамки рассмотренной задачи, так как осложнены дополнительными ограничениями.
Суммарный объем производства больше потребления - может быть введен фиктивный пункт потребления Вn+1 с объемом потребления
bn+1 = bn+1 – суммарный объем нереализованного продукта.
bn+1 – суммарный объем нереализованного продукта.
Размеры остатков в разных пунктах производства можно регулировать введением штрафа за единицу нереализованного продукта Аi.
Суммарный объем производства меньше потребления, то полное удовлетворение всех пунктов потребления невозможно. В этом случае необходимо организовать перевозки всего произведенного продукта так, чтобы наиболее важные пункты удовлетворялись полнее, и при этом суммарные транспортные расходы должны быть минимальны – вводится величина ущерба rj при неудовлетворении пункта Вj.
Требуется минимизировать суммарные затраты
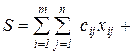
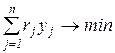
при условиях
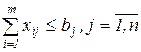 ,
, 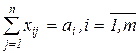 , xij > 0, yj = bj -
, xij > 0, yj = bj - 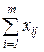 , где
, где
yj – разность между потребностями пункта Вj и поставками в него.
Перевозки с резервированием.
В некоторых районах пунктов производства может возникнуть необходимость в резервировании определенного количества продукта.
Iк – совокупность номеров i-го пункта производства в к-ом районе.
Требуется организовать перевозки таким образом, чтобы в к-ом районе (к=1,…,s) сохранилось не менее Vк единиц продукта.
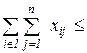
 - Vк ,
- Vк ,  .
.
Общее число продуктов, вывезенных из всех пунктов производства к-го района должно быть не менее, чем на Vк (величину заданного резерва) меньше суммарного количества продукта, произведенного в этом районе.
Задача сводится к задаче транспортного типа 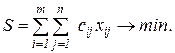
При условиях
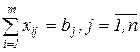 - удовлетворение спроса каждого пункта потребления;
- удовлетворение спроса каждого пункта потребления;
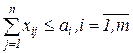 из каждого пункта потребления не может быть вывезено продукта
из каждого пункта потребления не может быть вывезено продукта
больше, чем производится;
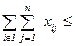
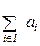 - Vк ,
- Vк ,  - условие резервирования;
- условие резервирования;
xij ≥ 0 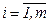 ,
, 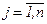 - объем перевозок неотрицательные числа (перевозки запрещены из пунктов потребления в пункты производства).
- объем перевозок неотрицательные числа (перевозки запрещены из пунктов потребления в пункты производства).
Пришли к задаче планирования перевозок, обеспечивающего удовлетворение спроса всех пунктов потребления, и гарантирующего сохранение требуемых резервов в каждом районе.
Ограничения на пропускные способности магистралей (в ограниченный промежуток времени) не позволят реализовать оптимальный план перевозок, полученный без учета этих ограничений.
В этом случае в транспортной задаче условие xij ≥ 0 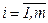 ,
, 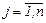 заменяется неравенством вида 0 ≤ хij ≤ dij, где dij – пропускная способность магистрали (ij), т.е. максимальный объем продукции, который может быть перевезен по этой магистрали за рассматриваемый промежуток времени. Такая задача может быть вообще неразрешимой (когда пропускная способность всех магистралей, ведущих к j-му потребителю меньше объема его потребностей).
заменяется неравенством вида 0 ≤ хij ≤ dij, где dij – пропускная способность магистрали (ij), т.е. максимальный объем продукции, который может быть перевезен по этой магистрали за рассматриваемый промежуток времени. Такая задача может быть вообще неразрешимой (когда пропускная способность всех магистралей, ведущих к j-му потребителю меньше объема его потребностей).
Перевозки с промежуточной обработкой.
Задача может быть осложнена наличием промежуточных транспортных узлов, в которых производится обработка груза (перевалка на другой вид транспорта, доработка полуфабриката перед поступлением его в пункт потребления).
А1,…, Аm – пункты производства с объемами производства а1, …, аm
В1,…, Вn – пункты потребления с объемами потребления b1,…, bn
С1,…, Ск – пункты промежуточной обработки.
Возможности пункта промежуточной обработки Сλ ограничены dλ единицами продукта.
Стоимости перевозки единицы полуфабриката продукта из Аi в Сλ составляет Сiλ‘, стоимость перевозки единицы полуфабриката продукта из Сλ в Вj составляет Сλj“.
Составить такой план перевозок, при котором весь полуфабрикат вывозится, полностью обрабатывается, потребности всех пунктов потребления удовлетворяются и при этом транспортные расходы минимальны.
Математическая модель.
Ziλj – количество продукта, доставляемое из пункта Аi в Вj через Сλ.
Транспортная таблица.
| B1 | B2 | … | Bn | Bn+1 | Bn+2 | … | Bn+k-1 | Bn+k | ||
| А1 | M | M | M | c’11 | c’12 | c’1,k-1 | c’1k | a1 | ||
| А2 | M | M | M | c’21 | c’21 | c’2,k-1 | c’2k | a2 | ||
| ... | … | … | ||||||||
| Аm | M | M | M | c’m1 | c’m2 | c’m?k-1 | c’mk | am | ||
| Аm+1 | c”11 | c”12 | c”1n | M | M | M | d1 | |||
| Аm+2 | c”21 | c”21 | c”2n | M | M | M | d2 | |||
| … | … | |||||||||
| Аm+k-1 | c”k-1,1 | c”k-1,2 | c”k-1,n | M | M | … | M | dk-1 | ||
| Аm+k | c”k1 | c”k2 | c”kn | M | M | M | dk | |||
| b1 | B2 | … | Bn | d1 | d2 | … | dk-1 | dk |
Определить план перевозок {Ziλj}, на котором достигается минимум линейной формы

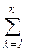
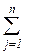 ( Сiλ‘ + Сλj“) Ziλj → min
( Сiλ‘ + Сλj“) Ziλj → min
при условиях
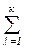
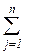 Ziλj = аi
Ziλj = аi 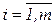

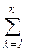 Ziλj = bj
Ziλj = bj 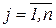

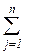 Ziλj ≤ dλ
Ziλj ≤ dλ 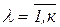
Ziλj ≥ 0, 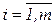 ,
, 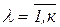 ,
, 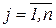
Необходимое и достаточное условие разрешимости задачи
 аi =
аi = 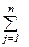 bj ≤
bj ≤ 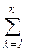 dλ
dλ
Преобразуем, введя новые переменные
xi,n+λ – количество полуфабриката, поступающее из пункта производства Аi в пункт обработки Сλ.
xm+λ,j - количество полуфабриката, поступающее из пункта обработки Сλ в пункт потребления Вj.
xi,n+λ =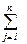 Ziλj ,
Ziλj , 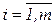 ,
, 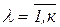 .
.
xm+λ,j =  Ziλj,
Ziλj, 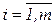 ,
, 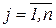 .
.
В новых переменных задача формулируется так: требуется минимизировать

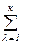 Сiλ‘xi,n+λ +
Сiλ‘xi,n+λ + 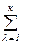
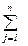 Сλj“ xm+λ,j
Сλj“ xm+λ,j
при условиях
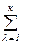 xi,n+λ = аi ,
xi,n+λ = аi , 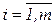 ,
,
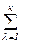 xm+λ,j = bj
xm+λ,j = bj 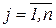 ,
,
 xi,n+λ =
xi,n+λ =  xm+λ,j ≤ dλ
xm+λ,j ≤ dλ 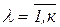
xi,n+λ ≥ 0, xm+λ,j ≥ 0, 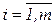 ,
, 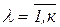 ,
, 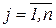 .
.
6.3 Распределительные задачи линейного программирования
Задачи распределения применяются при планировании множества операций, требующих одни и те же ресурсы и одно и то же оборудование. Предполагается, что каждая операция может быть выполнена многими способами, но для выполнения каждой операции наиболее подходящим путем не хватает ресурсов и оборудования. Задача заключается в том, чтобы, используя ограниченные мощности и наличные материалы, выполнить все работы оптимальным образом.
Задачи распределения в общем виде можно разделить на два вида:
1. Задан объем работ. Имеются определенные ресурсы, т.е. фиксированные производственные мощности и количество материалов. Необходимо найти такой вариант использования ресурсов, который обеспечит минимальные затраты на выполнение заданных работ;
2. Заданы определенные материалы и оборудование (ресурсы). Необходимо определить, какая работа дает максимальную прибыль при использовании этих ресурсов.
Несмотря на требование линейности функций критериев и ограничений, в рамки линейного программирования попадают многочисленные задачи распределения ресурсов, управления запасами, сетевого и календарного планирования, транспортные задачи и прочие. Рассмотрим некоторые из них.
Примеры распределительных задач.
План снабжения предприятий. Имеются сырьевые базы и предприятия-потребители. Требуется разработать такой план снабжения сырьем каждого предприятия (с какой базы, в каком количестве, каким видом транспорта и какое сырье доставляется), чтобы потребности в сырье были обеспечены при минимальных расходах на перевозки. Здесь показатель эффективности – суммарные расходы на перевозки сырья в единицу времени (R → min).
Постройка участка магистрали. При постройке участка магистрали в распоряжении имеется определенные средства (трудовые и материальные ресурсы), требуется спланировать строительство (распределить ресурсы) так, чтобы строительство было завершено в минимальный срок. Здесь необходимо учитывать случайные факторы (метеоусловия, отказы техники), и тогда показатель эффективности – среднее ожидаемое время окончания строительства (Т → min).
Сеть торговых точек. Требуется спланировать количество торговых точек, их размещение, товарные запасы, чтобы обеспечить максимальную экономическую эффективность распродажи. Здесь показатель эффективности – средняя ожидаемая прибыль от реализации товаров (П → mах).
Задача о комплексном использовании сырья. Исходное сырье или материал может перерабатываться различными технологическими способами. В каждом случае получается в различном сочетании несколько видов продукции. Требуется найти план переработки, при котором заданные объемы конечной продукции получались бы с наименьшими затратами исходных материалов. Одним из распространенных примеров применения этого типа задач является оптимальный раскрой материалов.
Противолодочный рейд. Требуется рационально организовать боевую операцию по уничтожению подводной лодки группой самолетов (выбрать маршруты самолетов, высоту полета, способ атаки). Здесь показатель эффективности – вероятность того, что лодка будет уничтожена.
Распределение изделий между предприятиями (оборудования между участками) – минимизация суммарных затрат на изготовление всех изделий с учетом времени производства;
Регулирование парка вагонов (распределение вагонов разных типов под различные грузы) -минимизация суммарных затрат на погрузку;
Выбор рациональных пропорций производства и использования энергоресурсов при минимуме затрат (объем добычи угля и план распределения различных сортов угля между энергетическими установками, обеспечивающий их потребности наиболее экономным путем).
Рассмотрим некоторые примеры.
Распределение транспортных единиц по линиям
Математическая модель (суммарные транспортные расходы минимальные) (ограничения по фондам времени каждой транспортной единицы)Выбор средств доставки грузов.
Через хij обозначим количество средств доставки типа j, отправляющееся из пункта i . Математическая модель (суммарные транспортные расходы минимальные)Задача о назначениях
Частным случаем транспортной задачи линейного программирования является задача о назначениях – задача выбора.
Это распределительная задача, в которой для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т.п.), а каждый ресурс может быть использован на одной и только работе.
То есть, ресурсы не делимы между работами, а работы не делимы между ресурсами.
Задача о назначениях имеет место при назначении людей на должности, водителей на машины, транспортных средств на маршруты, при распределении групп по аудиториям, тем по подразделениям.
Исходные параметры модели
Имеется n работ и n кандидатов для их выполнения (механизмов). Производительность каждого механизма различна. Затраты i-го кандидата на выполнение j-ой работы равны cij (i, j = 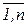 ).
).
Пусть хij – переменная, значение которой равно 1, если i-й кандидат назначен выполнять j-ю работу и 0 – в противном случае.
Математическая модель.
Найти минимум целевой функции

(в целевую функцию входят только те значения cij (i, j = 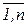 ), для которых хij отличны от нуля, т.е. входят затраты, соответствующие назначенным работам)
), для которых хij отличны от нуля, т.е. входят затраты, соответствующие назначенным работам)
при ограничениях
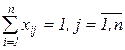 (каждый кандидат выполняет только одну работу);
(каждый кандидат выполняет только одну работу);
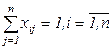 (каждая работа может выполняться одним кандидатом);
(каждая работа может выполняться одним кандидатом);
хij Є {0; 1}, (i, j = 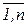 ).
).
Решить задачу о назначениях – значит найти хij, удовлетворяющие ограничениям и доставляющим минимуму целевой функции.
Это транспортная задача, в которой правые части ограничений равны 1, а переменные могут принимать только два значения (0,1). Простая форма задачи позволила разработать для нее достаточно простые методы решения.
Экономическая интерпретация задач линейного программирования.
Известны: общие запасы каждого ресурса, количество ресурсов каждого типа, затрачиваемое на изготовление одного изделия каждого вида, прибыль,… Возможная формулировка цели – максимизация прибыли, минимизация себестоимости,… Параметры задачи:Перевозки взаимозаменяемых продуктов
Если неоднородные продукты взаимозаменяемы (топливо разных сортов, или топливо одной и той же марки, добываемое в разных районах, цемент различных… Требуется составить план перевозок топлива разных сортов из пунктов… Пункт добычи нескольких различных сортов топлива рассматривается как несколько различных пунктов производства (число…Перевозка неоднородного продукта на разнородном транспорте.
Расстояние от места расположения g-го автохозяйства (g = 1,…., s) до пункта производства i-го груза (i = 1,…, m) известно. Известна скорость машин… Параметры модели agк – количество машин к-го типа в g-ом автохозяйстве;Основные определения
Основная особенность управления - целенаправленность. Управляемая система создается для достижения тех или иных целей (самолет, ракета, управление… Рассмотрим основные определения системы с управлением на примере… Функциональная схема системы – символическое изображение всех функциональных элементов технологического процесса и…Формальная запись системы с управлением
Модели систем без управления описывают динамические процессы (с помощью, например, дифференциальных уравнений), которые не содержат свободных… Модели систем с управлением разрабатываются для оптимизации некоторых действий… Рассмотрим систему с управлением, которая описывается обыкновенными дифференциальными уравнениями ˙z = f (z, u,…Модели систем автоматического управления
При автоматическом управлении качество процесса управления обеспечивает регулятор: обеспечивает поступление управляющих сигналов в зависимости от… Дадим основные определения системы автоматического управления на примере… При автоматическом управлении воздействие на управляемый орган осуществляет специальное управляющее устройство.Устойчивость движения систем
Чтобы определить, устойчиво ли состояние равновесия какой-либо системы, изучается поведение этой системы при малых отклонениях от равновесия. Под возмущающими факторами понимаются силы, не учитываемые при описании… Система обычно находится в состоянии движения, поэтому рассматривают устойчивость движения. Проблема исследования…Определение программного движения и управление движением
Таким образом, появились две тесно связанные между собой задачи – определение программного движения и управление этим движением. Из необходимости решения проблемы расчета траектории, обеспечивающей… Разделение процесса управления на управление программным движением и последующую коррекцию с помощью механизмов…Модели автоматизированных систем управления
Различают два основных типа автоматизированных систем управления: системы управления производственными процессами и системы… Главные отличия этих двух типов – в характере объекта управления и форме… В системах управления технологическими процессами объекты управления – машины, процессы, приборы, устройства, форма…Формализованная схема дискретного производственного процесса.
Производственный процесс расчленяется на элементарные акты, достаточно простые и удобные с точки зрения подбора соответствующих математических схем.
Строится математическое описание каждого элементарного акта и взаимодействия между ними, характеризующего совокупность элементарных актов как единый процесс.
Наиболее существенные элементарные акты реального производственного процесса – производственные (технологические) операции. Например, технологические операции обработки, сборки, контроля качества.
Типичные абстрактные операции, соответствующие достаточно широкому классу производственных операций: операции обработки, сборки и управления.
Между производственной операцией и формализованной операцией не всегда однозначное соответствие – данная реальная элементарная производственная операция для формализации может быть достаточно сложной, тогда ее описывают с помощью совокупности нескольких формализованных операций. В общем виде расчленение производственного процесса на элементарные акты не решается – это делается в зависимости от конкретных обстоятельств.
Выполнение производственной операции над системой (изделием, полуфабрикатом) обязательно связано с изменением ее свойств, описываемых числовыми характеристиками или параметрами, т.е. выполнение операции связано с изменением значений параметров системы.
Каждая производственная операция может быть представлена как оператор, определяющий изменение фазовых координат (значений параметров) системы во времени. Тогда математическая модель производственной операции может быть представлена как модель динамической системы (детерминированная или стохастическая), а модель производственного процесса - как многоуровневая динамическая модель.
Математическое описание элементов производственного процесса основано на наборе параметров, характеризующих систему (полуфабрикаты, заготовки, детали, узлы и т.д.). В дальнейшем объект, над которой совершается производственная операция, будем называть полуфабрикатом.
Среди характеристик полуфабрикатов будем различать координаты состояния (изменяются по ходу производственного процесса в результате производственных операций) и фиксированные параметры (в рамках данного производственного процесса).
Сущность формализации операции состоит в переработке информации, описывающей состояния участвующих в операции полуфабрикатов.
Операции обработки
Абстрактная операция обработки – такой элементарный акт производственного процесса над полуфабрикатом, в результате которого меняется хотя бы одна из координат состояния полуфабриката.
Реальные технологические операции обработки: изменения размеров полуфабриката (обработка резанием, ковка, штамповка и т.д.), положения в пространстве (транспортировка, повороты), сообщение полуфабрикату дополнительного признака (окрашен, проверен) и т.д.
В качестве операции обработки могут быть формально представлены некоторые естественные акты производственного процесса, обычно не относящиеся к операциям, например, остывание (заготовки из печи), высыхание, окисление.
Под операцией обработки можно также понимать любые объединения последовательных подобных актов, особенно если они относятся к одному оборудованию.
Каждая операция обработки выполняется вполне определенным формализованным станком, обеспечивающим выполнение операции обработки (независимо от его реальной структуры и назначения).
Станок - любой комплекс производственного оборудования.
Математическое описание операции обработки - установление соотношений между параметрами, характеризующими взаимодействие станка и полуфабриката в процессе обработки.
Считаются известными:
- значения всех координат состояния полуфабриката aк (a1 , a2 , , . . . , as ) до начала операции (для момента времени t ≤ tн);
- параметры станка βl (β1, β2, . . . , βg);
- режим функционирования станка во времени
tн - момент начала операции обработки;
τоп - длительность операции;
τг - время, подготовки станка следующей операции;
tг = tк + τг - момент готовности станка к выполнению операции;
tк = tн + τоп - момент окончания операции обработки.
Требуется определить:
значения всех состояний полуфабриката aкоп после операции (для моментов времени t ≥ tк)
aкоп = aкоп (a1 , a2 , . . . , as , β1, β2, . . . , βm).
В общем случае aкоп представляют собой случайные величины: случайными могут оказаться параметры полуфабриката aк, или параметры станка βl; или, наконец, функции aкоп (случайные изменения в процессе выполнения операции). Простейшая формализация такого случайного процесса:
aкоп = aкоп0 (a1 , a2 , , . . . , as, β1, β2, . . . , βm) + δ коп,
где δ коп – случайные отклонения величины aкоп от некоторого неслучайного значения aкоп0, заданные соответствующими законами распределения.
Введем обозначения для режима функционирования станка во времени:
i – номер станка (агрегата, линии);
j – номер экземпляра полуфабриката заданного типа;
tjп - момент поступления j-го экземпляра полуфабриката к станку.
Одним из наиболее существенных параметров любого полуфабриката является начальный момент времени, начиная с которого рассматривается история полуфабриката в связи с данным производственным процессом.
Часто t1j – момент поступления j-го экземпляра полуфабриката к первому станку – также и является начальным моментом истории полуфабриката, т.е. моментом его появления в производственном процессе.
В случаях, когда необходимо отличать момент первого появления полуфабриката в производственном процессе от момента его появления к первому станку, будем его обозначать t0j. Например, t0j – момент выхода заготовки из нагревательной печи, t1j – момент поступления ее к устройству, где выполняется первая операция, t2j – момент поступления к устройству, где выполняется вторая операция, и т.д.
Последовательности моментов tj поступления полуфабрикатов к станку могут быть детерминированными и случайными. В первом случае момент tj жестко определяется закономерностями синхронизации отдельных операций в данном производственном процессе (используется зависимость, позволяющая определить tj через другие известные величины, например, через tj-1), во втором – с учетом случайных колебаний величин tj.
Рассмотрим некоторые распространенные предположения относительно моменте начала операции tн.
Операции обработки с нецентрализованным управлением производственных циклов во времени.
Операция может начаться в любой момент, если только выполнены необходимые для этого условия: станок готов к работе, и к нему уже поступил очередной полуфабрикат. Момент начала операции равен моменту поступления, если к этому времени станок готов к операции, и равно времени конца предыдущей операции плюс время подготовки станка – если станок не готов к операции:
tjп если tj-1к + τ j-1 г ≤ tjп
tjн = { tj-1к + τ j-1 г если tj-1к + τ j-1 г > tjп
Любые дополнительные простои станка, связанные с особенностями производственных циклов, могут быть учтены соответствующим обобщением понятия τг, т.е. включены в τг.
Операции обработки с централизованным управлением производственных циклов (например, режим работы станков линий обработки деталей жестко синхронизован с режимом сборки изделий на конвейере).
Операция обработки может начинаться только в моменты времени, отстоящие друг от друга на величину длительности такта τТ. Допустимыми моментами начала операции могут быть только моменты времени вида t0 + kτТ, где t0 - начало отсчета времени, k = 0, 1, 2, .... Естественно, что операция может начаться в любой из указанных моментов, если к этому времени станок готов к работе, и уже поступил очередной полуфабрикат, т.е. tк + τг < tп.
В общем случае времена подготовки станка к следующей операции τг, длительности такта τТ, длительности операции τоп могут рассматриваться как случайные величины с заданными законами распределения.
Время подготовки станка к следующей операции зависит от характеристик самого станка и от характеристик полуфабрикатов (отдельные полуфабрикаты или структура их совокупности могут иметь такие особенности, которые способствуют увеличению времени на подготовку станка к выполнению следующей операции).
Длительности операции зависит обычно как от свойств станка, так и от состояния и параметров полуфабрикатов. Например, длительность обработки металлов резанием зависит от размеров полуфабриката, а длительность горячей штамповки – от температуры и т. д.
Операции сборки
Абстрактная операция сборки предполагает участие нескольких (не менее двух) полуфабрикатов (в отличие от операции обработки). Среди них необходимо различать ведущий полуфабрикат (сборный узел) и ведомые полуфабрикаты (детали, присоединяемые к узлу). Выбор одного из полуфабрикатов в качестве ведущего иногда оказывается условным, особенно для первых сборочных операций.
Под операцией сборки понимается такой элементарный акт производственного процесса над совокупностью полуфабрикатов (ведущим и ведомыми), в результате которого изменяется значение хотя бы одной из координат состояния ведущего полуфабриката (за счет присоединения к нему ведомых), а соответствующие ведомые полуфабрикаты прекращают существование.
Предполагается, что существует соответствующий набор производственного оборудования, обеспечивающий выполнение операции сборки.
Пусть в сборке участвуют узел (ведущий полуфабрикат, его состояние аку) и т деталей (ведомых полуфабрикатов). Координаты состояний их для моментов времени t ≤ tн обозначим ау1, ау2, ..., аут.
В результате операции сборки сборный узел имеет новые значения координат аску, а детали прекратят существование.
Для построения математического описания операции сборки в первую очередь необходимо задать соотношения вида
аску = аску (ау1, ау2, ..., аут, β1, β2, . . . , βс).
где βl – параметры сборочного оборудования.
Моменты прекращения существования деталей, использованных на сборке, определяются лишь в случае необходимости.
Для случайных процессов сборки по аналогии с операцией обработки используются соотношения
аску = аску0 (ау1, ау2, ..., аут, β1, β2, . . . , βl) + δаску.
где δаску – случайные отклонения, задаваемые соответствующим законом распределения или другими вероятностными характеристиками.
Анализ параметров, определяющих синхронизацию процесса операции сборки.
Момент начала операции tн. Используются различные предположения, связанные с готовностью к сборке (по аналогии с рассмотренной ранее готовностью к обработке).
Операция начинается в момент готовности всей совокупности элементов: tпу – момент поступления на сборку узла, tпi1, tпi2, ..., tпim — моменты поступления деталей. По аналогии с операцией обработки tнj = max {tпу, tпi1, tпi2, . . . , tпm, tkj-1, + τi-1г}.
Более сложный случай - отдельные сборочные работы (части операции сборки) начинаются по мере поступления на сборку тех или иных деталей или по мере готовности соответствующих элементов производственного оборудования. Этот случай может быть сведен к предыдущему, более простому, если операцию сборки расчленить на несколько последовательно выполняемых операций.
При синхронизированном режиме операция начинается только в момент начала рабочего такта сборочного оборудования - по аналогии с операцией обработки tн = t0 + (к + 1) τТ.
Длительность операции τоп - операция сборки представляется в виде последовательных этапов: установка деталей на узле τу, крепление деталей τкр, регулировка узла τрег. Каждое трех слагаемых в общем случае является случайной величиной с заданными вероятностными характеристиками.
Другие характеристики, связанные с взаимодействием элементов процесса во времени, например, время такта τТ, время подготовки к операции τг и др., могут быть описаны при построении формализованной схемы таким же образом, как это было сделано применительно к операции обработки.
Особенностью формализации операции сборки является некоторая «неравноправность» участвующих в сборке полуфабрикатов – предпочтение всегда отдается сборному узлу по сравнению с деталями. Например, при описании следствий тех или других действий судьба сборного узла всегда описывается с исчерпывающими подробностями, в то время как относительно судьбы каждой отдельной детали информация обычно оказывается ограниченной. Часто можно обойтись фиксацией состояний только сборного узла, а состояния деталей не фиксировать.
Операции управления
Операции управления сами по себе не изменяют состояния полуфабрикатов и непосредственного отношения к обработке и сборке не имеют - в результате операций управления вырабатывается информация, необходимая для согласованной работы отдельных составляющих элементов производственного комплекса.
Примеры операций управления: регулирование скорости производственного процесса, регулирование параметров, характерных для той или другой операции (усилий, температуры и т.п.), распределение полуфабрикатов между параллельно работающими станками или линиями, выработка признаков прекращения или возобновления подачи полуфабрикатов к станку или линии в зависимости от длины очереди, контроль хода производства и качества продукции и т. д.
Предполагается существование оборудования (управляющее устройство, человек-оператор), которое обеспечивает выполнение операции управления.
В результате операции управления вырабатывается информация о требуемых изменениях технологических режимов и структуры производственного процесса для рассматриваемого комплекса оборудования. Эта информация может быть представлена в виде поправок ∆βк к параметрам производственного оборудования. Осуществляется привязка операции управления ко времени выполнения самой производственной операции.
Операция управления начинается после поступления полуфабриката и заканчивается до начала производственной операции - применяется в случае, если наибольшее влияние на ∆β оказывают параметры поступающего полуфабриката ак (главная задача управления – настроить станок на режим, соответствующий параметрам поступающего полуфабриката).
Операция управления начинается после окончания производственной операции – применяется в случае, когда задача управления состоит в поддержании стабильных значений состояний поступающего полуфабриката ак или стабильных режимов работы оборудования βl, а ∆β определяется значениями величин состояния полуфабриката ак и параметров станка βl.
Операция управления и производственная операция выполняются одновременно.
Формализуются случаи возможных ошибок, сопровождающих операции управления (случайными функциями могут быть как состояния и параметры станка, так и сама ∆β). Для описания ошибок используются обычные методы задания вероятностных характеристик.
Формализация отклонения течения производственного процесса от нормального
Расстройства режима синхронизации производственного процесса При идеальной синхронизации производственного процесса операция над j-ым… На практике такое равенство часто нарушается: интервалы времени, определяющие синхронизацию элементарных актов…Моделирование комплексного процесса обработки, сборки и управления при поточном производстве
Линия сборки (совокупность устройств, обеспечивающих сборку изделия) состоит из l устройств. Каждое устройство выполняет только одну сборочную… На сборку поступают ведущий полуфабрикат (основа сборного узла) и… Будем предполагать, что режим перемещения сборного узла от места выполнения одной операции к месту выполнения…Формализованная схема непрерывного производственного процесса.
Предположим, что рассматриваемый непрерывный производственный процесс реализуется на некоторой установке (оборудовании), характеризующейся параметрами γк, к = 1, 2, ..., k* (например, емкость пли весовая вместимость резервуаров, сечения входных, промежуточных и выходных отверстий, объемы промежуточных бункеров, силовые и энергетические характеристики приводов и т. д.).
К установке поступают т компонент сырья с интенсивностями прихода μi i= 1, 2, ..., m (единицы веса или объема в единицу времени), и параметрами ai1, ai2, ..., airi. Установка выдает п компонент готовой продукции с интенсивностями выхода νj, j = 1, 2, ..., п, и параметрами сборочной установки βj1, βj2, . . . , βjlj.
Процесс, происходящий в установке, характеризуется параметрами (реагирования)
δs, s = 1, 2, ..., s*.
При этих обозначениях математическим описанием процесса могут служить соотношения
νj = νj (μi, ai, γк, δs, βj),
βj1 = βj1 (μi, ai, γк, δs, νj), (1)
. . . . . . . . . . . . . . . . . .
βjlj = βjlj (μi, ai, γк, δs, νj),
описывающие зависимость каждого из параметров νj, βj компонент готовой продукции от параметров сырья, установки и процесса.
Все величины, фигурирующие в этих соотношениях, могут быть функциями времени, а сами соотношения – явно зависеть от времени t.
Кроме того, эти соотношения могут быть случайными в том смысле, что каждой совокупности значений аргументов ставится в соответствие не одно определенное значение параметра, входящего в левую часть соотношений, а закон распределения вероятностей для значений этого параметра.
В некоторых случаях эти соотношения могут быть дополнены рядом соотношений весового или объемного баланса, например, сумма количеств поступающих компонент сырья равна сумме выдаваемых количеств компонент продукции; сумма количеств поступающих компонент сырья равна сумме емкостей резервуаров или бункеров и т.д. Однако соотношения количественного баланса не всегда нужны, поскольку в процессе могут фигурировать неучитываемые отходы.
Формализованная схема процесса управления.
Рассмотренная схема приспособлена для учета технологических факторов при описании непрерывного производственного процесса, но в явном виде не учитывает факторов управления производством. Чтобы ослабить значение этого обстоятельства, к приведенным соотношениям (1) добавляются операторы или алгоритмы переработки информации, свойственные процессу управления производством.
Эти соотношения рассматриваются отдельно от модели технологической части процесса и выносятся в особую формализованную схему. При этом возникает проблема взаимодействия обеих формализованных схем, Для ее разрешения в первую очередь необходимо согласовать выходы схемы управления со входами технологической схемы.
Это достигается выделением специальных параметров управления из числа параметров, фигурирующих в математическом списании технологической части модели. В самом деле, управление непрерывным производственным процессом сводится к регулированию количества и свойств сырья, поступающего к установке (параметры airi и интенсивности прихода μi) регулированию условий протекания процесса (параметры δs), а иногда - изменению параметров γк установки, реализующей непрерывный производственный процесс, или регулированию количества и свойств готовой продукции (параметры отбора компонент продукции - интенсивностями выхода νj, j = 1, 2, ..., п, и параметрами сборочной установки βj1, βj2, . . . , βjlj).
Выделенные таким образом параметры управления можно разбить на группы, соответствующие оперативному управлению установкой, оперативному управлению группой установок или предприятием в целом, текущему и перспективному планированию и т. д.
Производственные процессы, представляющие практический интерес, как правило, не относятся ни к дискретному, ни к непрерывному типам.
Чаще всего на практике производственные процессы состоят из нескольких дискретных и непрерывных частей. Например, могут быть случаи, когда все или некоторые технологические операции (подпроцессы) носят непрерывный характер, в то время как остальные (нетехнологические) производственные операции (транспортировка сырья и продукции, упаковка, проверка и т. д.) имеют дискретный характер.
В соответствии с формализованной схемой и соотношениями (1) характеристики процесса (например, интенсивности выхода νj и параметры сборочной установки βj) зависят от его параметров (μi, ai, γк, δs и т. д.). Некоторые из перечисленных параметров процесса являются параметрами управления и не могут быть заданы в виде исходных данных или начальных условий. Однако знание всех параметров оказывается необходимым условием для моделирования процесса.
Поэтому параметры управления должны быть заданы (как функции времени t) для всего интервала моделирования процесса, либо в модели должны присутствовать подалгоритмы, реализующие модель системы управления, по крайней мере в части выдачи управляющих команд в зависимости от состояний процесса и внешних воздействий (например, указаний руководящих и планирующих органов).
Практически моделирующие алгоритмы обычно содержат подалгоритмы, относящиеся как к технологической, так и к управляющей частям.
Реализация на ЭВМ моделирующего алгоритма, основанного на точном воспроизведении соотношений (1), наталкивается на значительные трудности в связи с отсутствием в общем случае точных методов решения соответствующих уравнений, содержащих нелинейные и стохастические зависимости. Поэтому, как правило, приходится прибегать к дальнейшим упрощениям и огрублениям постановки задачи и математической модели.
В частности, при реализации соотношений вида (1) все переменные в интервале ∆t могут заменяться постоянными, равными средним значениям рассматриваемых величин в этом интервале. Изменения значений переменных происходят скачком в моменты времени, соответствующие моментам перехода к очередным ∆t. Для уменьшения влияния ошибок, связанных с такого рода огрублением математического описания процесса, пользуются особого рода средними значениями переменных, определяемыми из условия минимума суммарных ошибок.
Рассмотрим особенность моделирования непрерывных производственных процессов, связанную с реализацией случайных операторов вида (1).
При прямом подходе процедура моделирования сводится к синтезу закона распределения соответствующего параметра как случайной величины и выбору значения параметра по жребию в соответствии с этим законом распределения. Такая процедура оказывается чрезвычайно громоздкой главным образом за счет операций, связанных с построением закона распределения.
Для упрощения процедуры моделирования удобно преобразовать соотношения (1) таким образом, чтобы искомый параметр представлялся в виде детерминированной функции от других параметров и некоторой фиктивно вводимой случайной величины ξ с заданным законом распределения.
Например,
νj = νj* (μi, ai, γк, δs, βj, ξ). (2)
В этом случае возможное значение ξ формируется по общим правилам преобразования случайных чисел, а параметр νj вычисляется как вполне детерминированная функция своих аргументов.
Моделирующий алгоритм для непрерывного производственного процесса содержит операторы, уравнивающие значения параметров для каждого ∆t в соответствии с соотношениями формализованной схемы (1) или (2).
9 СИНТЕЗ МОДЕЛИ (ПРОЕКТА) СИСТЕМЫ
9.1 Проектирование системы как процесс создания (синтеза) ее модели
Моделирование системы предвосхищает ее создание – прежде, чем что-либо создать, необходимо построить и исследовать модель будущей системы – проект системы, на основании которой будет создаваться система.
Проектирование связано с понятием развития системы: в системе могут накапливаться противоречия, для разрешения которых необходима модернизация существующей или создание новой системы. В любом случае это требует разработки проекта системы.
В зависимости от конкретной задачи существуют различные определения понятия «проект».
В самом общем современном понимании: проект (англ. project) – это что-либо, что предполагается осуществить - разработка новой техники или технологии, создание (сооружение) объекта, реконструкция или создание предприятия, программа работ (образовательных, исследовательских, социальных, культурных, развития региона) и т.п.
Принятое узкое понимание: проект (англ. design) – документально оформленная модель будущей системы, достаточная для создания системы с заданными свойствами.
В ряде крупных отраслей создаваемые объекты являются настолько сложными, что работа над ними осуществляется не в составе проектов, а в составе Программ, которые можно определить как совокупность проектов или проект особой сложности (программы развития авиационно-космической, машиностроительной, оборонной отраслей, топливно-энергетического комплекса, жилья, региона и др.).
Объектами проектирования могут быть системы или процессы (процессы управления, технологические процессы).
В соответствии с двумя видами задач системных исследований – анализом и синтезом – и с целевой предназначенностью моделей как средства отображения свойств объекта выделяют два вида модели – познавательную и предписывающую.
Различия между познавательной и предписывающей моделями: в познавательной - модель отражает реальность, в предписывающей – реальность отражает модель.
Примеры предписывающей модели – правила дорожного движения, проекты систем.
Проект системы представляет собой предписывающую модель системы – по этой модели должна быть создана система. При проектировании решается задача синтеза – преобразование исходного описания в модель с заданными свойствами. Проект всегда имеет цель – достижение определенных результатов при решении какой либо проблемы, удовлетворении возникших потребностей.
В основе синтеза - определение в системе структурных отношений, характеризуемых упорядоченностью, организованностью взаимодействий между отдельными ее уровнями по вертикали.
Три этапа решения задачи синтеза:
- выявление глобальной функции системы (абстрактный синтез – рассмотрение системы на абстрактном уровне в виде черного ящика, о котором известно только то, что он будет делать),
- разработка структуры системы, реализующей необходимые функции (структурный синтез – преобразование функционального описания в структурное - разбиение глобальной функции системы на подфункции до тех пор, пока не будут получены элементарные функции, структуры которых очевидны, или уже реализованы);
- определение параметров системы так, чтобы получить желаемое качество системы.
Желаемое качество системы можно обеспечить:
- улучшением качества входящих в систему элементов (параметрический метод);
- изменением структуры системы (схемотехнический метод);
- уменьшением отрицательного влияния внешней среды (воздействием на внешние параметры).
В основе структурного моделирования – совместное применение методов анализа и синтеза.
При анализе объект разделяется на части и каждая из них исследуется в отдельности, при синтезе решается обратная задача - соединение частей в целое. При этом важно не просто разбить целое на элементы, но и соединить эти элементы таким образом, чтобы они снова образовали единое целое. В результате синтеза как завершающего этапа процесса «анализ – синтез» создается структура системы.
Единство анализа и синтеза как основа системного анализа относится ко всем отраслям знаний, в т.ч. к моделированию. Алгоритмов «анализа – синтеза» как известно, нет – определена только общая методология (как выполняются операции анализа и синтеза).
Основная операция системного анализа (неформальная) – декомпозиция (разделение целого на части). Применительно к построению структуры модели – определение состава модели (компонентов).
Компонент – любая часть предметной области, которая может быть выделена как некоторая самостоятельная сущность. Это и система (модель) в целом, и любая часть системы (модели) – подсистема, элемент.
Основная сложность декомпозиции – определение базовых (неделимых) моделей компонентов, соотношение моделей микро- и макроподхода. В основе декомпозиции – достижение компромисса между полнотой набора формальных моделей рассматриваемой системы и простотой – он может быть достигнут, если в модель включаются только модели компонентов, существенных по отношению к цели моделирования.
Примеры: построение монтажной радиосхемы, построение вычислительного агрегата из набора однотипных элементов, исследование твердости материалов (графита и алмаза), состоящих из однотипных элементов (атомов) но с разными способами соединения атомов (кристаллическими решетками).
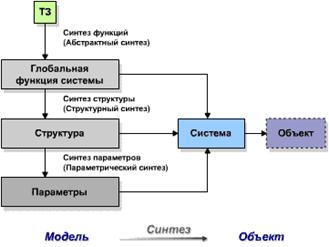
Этапы синтеза объекта
Проектирование – процесс создания формализованного описания (модели) системы.
Цель проектирования - создание системы, которая удовлетворяет:
- заданным функциональным свойствам с учетом существующего уровня знаний, развития технологий, ограничений по стоимости системы;
- требованиям по продолжительности и стоимости самого процесса проектирования.
Проектирование и создание сложных систем с учетом будущих условий функционирования системы в изменяемой внешней среде вызвало необходимость анализа больших объемов информации и принятия адекватных решений.
При синтезе системы (проектировании) основные задачи моделирования еще не созданной системы и проведения вычислительных экспериментов применяются:
- для оценки эффективности будущей системы, а также определения чувствительности характеристик системы к изменениям структуры, алгоритмов и параметров объекта моделирования и внешней среды;
- для синтеза и анализа различных вариантов системы и выбора среди конкурирующих такого варианта, который удовлетворял бы заданному критерию оценки эффективности системы при принятых ограничениях;
- для получения информации, дополняющей результаты натурных испытаний реальной системы после ее создания, и для получения прогнозов эволюции системы во времени.
Гибкость модели должна давать возможность воспроизведения различных ситуаций при варьировании структуры, алгоритмов и параметров системы.
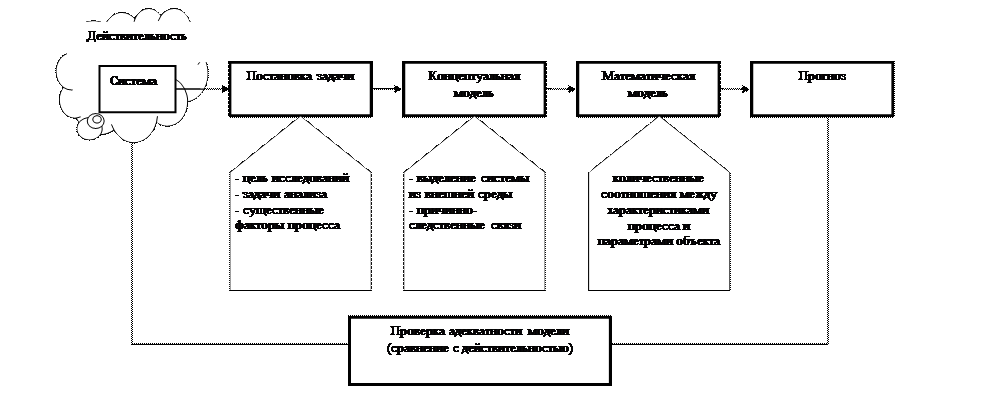
Схема построения познавательной модели
Познавательная модель создается для изучения свойств системы с известной структурой и функциями - осуществляется анализ системы, устанавливаются изменения параметров системы (зависимость выходных параметров от входных).
Познавательная модель является формой представления знаний и построение ее направлено на приближение модели к реальности, которую она отображает (построение модели адекватной реальности), – при обнаружении расхождения между моделью и реальностью модель изменяется так, чтобы приблизиться к реальности. С помощью полученной модели делается прогноз развития процесса функционирования системы.
 |
Схема построения предписывающей модели
Предписывающая модель создается с целью построения новой системы (модернизации существующей) с заданными свойствами или для выполнения готовой системой заданных действий (решение задачи синтеза) - воспроизвести характеристики объекта, определяющие его поведение, реализующее цель создания новой системы.
Предписывающая модель является формой представления действий будущей системы, и построение ее направлено на приближение системы к модели – при обнаружении расхождения между реальностью и моделью, реальность (новая система с заданными свойствами) изменяется так, чтобы приблизиться к ее модели.
Схема построения предписывающей модели для создания системы:
- определяется цель создания новой системы и выделяются ее основные функции (интегративные свойства);
- строится последовательность функций компонентов, необходимая для проявления нового интегративного свойства;
- под функции подбираются (проектируются) компоненты, которые могут их осуществлять;
- оптимизируются параметры каждого компонента исходя из наилучшего выполнения заданной цели системы (процесс проектирования системы).
Адекватность системы и предписывающей модели исследуются с помощью познавательной модели, и возможные сценарии использования системы во внешней среде уточняется с помощью предписывающей модели.
Проектирование рассматривается как творческий неформальный процесс выработки и принятия решений на всех стадиях, начиная от принятия решения о необходимости создания системы, выбора ее структуры и параметров.
Проектное решение - промежуточное описание объекта, позволяющее определить дальнейшие направления работ (или окончание проектирования).
Проектные решения принимаются на всех этапах проектирования на основе опыта, интуиции, знания, ответственности лица, принимающего решение, с учетом вновь получаемой в процессе проектирования новой информации. Основа получения необходимой информации – математическое моделирование.
Всем процессам принятия решений присущи две основные черты: решение принимается для вполне определенной цели, из множества вариантов выбирается один, вполне определенный, отвечающий выдвинутым требованиям.
Какие требования выдвинуть к системе, какие технические решения необходимо в нее заложить, чтобы при дальнейшей модернизации она оставалась эффективной? Что такое эффективная система?
При проектировании сложных систем и их подсистем возникают многочисленные задачи, требующие оценки количественных и качественных закономерностей процессов функционирования таких систем, проведения структурного алгоритмического и параметрического их синтеза.
Проектирование – процесс создания формализованного описания (модели) системы.
Цель проектирования - создание системы, которая удовлетворяет:
- заданным функциональным свойствам с учетом существующего уровня знаний, развития технологий, ограничений по стоимости системы;
- требованиям по продолжительности и стоимости самого процесса проектирования.
Различные виды моделирования используются на всех этапах создания сложных систем (проектирование, внедрение, эксплуатация и эволюция) дл учета следующих особенностей:
- сложность структуры и стохастичность связей между элементами, неоднозначность алгоритмов поведения при различных условиях,
- большое количество параметров и переменных, неполноту и недетерминированность исходной информации;
- разнообразие и вероятностный характер воздействий внешней среды.
Ограниченность возможностей экспериментального исследования при создании сложных систем делает необходимым разработку методов их моделирования, которая позволила бы в соответствующей форме представить процессы функционирования систем, описание протекания этих процессов с помощью математических моделей, получение результатов экспериментов с моделями по оценке характеристики исследуемых объектов.
На разных этапах создания и использования систем для всего многообразия входящих в них подсистем применение моделирования преследует конкретные цели, а эффективность моделирования зависит от того, насколько грамотно разработчик использует возможности моделирования.
Выбор метода моделирования и необходимая детализация моделей существенно зависят от этапа разработки сложной системы. На этапах обследования объекта управления, например промышленного предприятия, и разработки технического задания на проектирование автоматизированной системы управления, модели в основном носят описательный характер и преследуют цель наиболее полно представить в компактной форме информацию об объекте, необходимую разработчику системы.
На этапах разработки технического и рабочего проектов систем, модели отдельных подсистем детализируются, и моделирование служит для решения конкретных задач проектирования, т. е. выбора оптимального по определенному критерию при заданных ограничениях варианта из множества допустимых. Поэтому в основном на этих этапах проектирования сложных систем используются модели для целей синтеза.
Целевое назначение моделирования на этапе внедрения и эксплуатация сложных систем — это проигрывание возможных ситуаций для принятия обоснованных и перспективных решений по управлению объектом.
Моделирование (имитацию) также широко применяют при обучении и тренировке персонала автоматизированных систем управления, вычислительных комплексов и сетей, информационных систем в различных сферах. В этом случае моделирование носит характер деловых игр. Модель, реализуемая обычно на ЭВМ, воспроизводит поведение управляемого объекта и внешней среды, а люди в определенные моменты времени принимают решения по управлению объектом.
9.2 Методология проектирования
Проектирование - это постепенный и итеративный процесс, который требует творчества, опирается на опыт и компетентность, идет путем проб и ошибок. И, тем не менее, использование сложившейся методологии проектирования вносит в процесс определенную организованность.
Проектирование осуществляется на основе выполнения комплекса работ поискового, исследовательского, экспериментального, расчетного, конструкторского характера. В такой постановке проектирование – процесс переработки информации.
Методы построения процесса проектирования включают методы и средства, позволяющие построить, организовать и управлять процессом проектирования, рассматривая его (процесс проектирования) как систему, функционирующую в определенных внешних условиях и ограничениях (к тому же изменяющихся во времени).
Проектирование - никак не точная наука. Не существует рецептов, которые могли бы заменить ум, опыт и хороший вкус в проектировании, различные фазы проектирования неотделимы друг от друга. Даже в Японии на начальной стадии проектов "все еще по большей части полагаются на неформальный подход - карандаш и бумагу".
Отсюда задачи автоматизации проектирования – выполнение рутинной работы, информационное обеспечение проектирования. Эти системы должны включать в себя развитые средства накопления и использования знаний, возможности параллельного ведения проектов, разделения по стадиям, подсистемам и т.д. Они должны обеспечивать хранение и доступ к информации; поддерживать логические связи; обеспечивать многофункциональную среду проектирования, предполагающую быстрый, легкий и надежный обмен проектными данными.
Методы представления объекта проектирования включают методы и средства, позволяющие описать и представить сам объект проектирования и различные его свойства (описательная модель). Это методы математического, графического, алфавитно-цифрового представления объекта проектирования.
Многоэлементность и разнообразие состава системы, различные типы, виды и классы подсистем, большое число внутренних и внешних связей, определяют большую размерность задачи проектирования, что делает невозможным создание единых формализованных методов проектирования.
Методология и методы проектирования (синтеза) системы определяются сложностью системы и особенностями процесса проектирования.
Различают общую и специальную методологии проектирования.
Общая методология проектирования для всех типов систем основана на представлении процесса проектирования как процесса системных исследований, рассматривает методы построения процесса проектирования и методы представления объекта проектирования.
При системных исследованиях в процессе проектирования широко используются наработанные методы и процедуры других дисциплин: экономических, исследования операций, теории информации и др., они основываются на современных технологиях автоматизированного проектирования, имеющемся программном, методическом и информационном обеспечениях, развитие которых также стимулируется вновь возникающими потребностями проектирования новых сложных систем.
Применение системного подхода в проектировании предполагает рассмотрение проектируемой системы как элемента системы более высокого уровня, во всем многообразии ее связей с внешним миром, что обеспечивает расширение множества вариантов, среди которых осуществляется выбор, с одновременным указанием способов отбрасывания наименее приемлемых - повышает обоснованность принимаемого проектного решения. Пренебрежение системным подходом приводит к принятию безграмотных проектных решений порой с непоправимыми последствиями, всё более губительными по мере того, как у лиц, принимающих решение, появляются большие возможности. Примеров подобных последствий, к сожалению, предостаточно.
С позиций системного подхода проектирование – это процесс перехода из исходного состояния (потребности, проблемы) в конечное (удовлетворение потребностей, решение проблемы) с учетом возможностей выполнения (обеспечений и ограничений).
Вход - потребности, выход - удовлетворенные потребности. Обеспечение - кадровый и научно-технический потенциал. Ограничения - финансовые, нормативно-правовые, этические, время, уровень качества, внешнее окружение.
Основные принципы системного подхода при построении моделей на этапе внешнего проектирования:
- модель строится как единое целое, все элементы, связи, действия системы подчинены достижению конечной цели (каждый компонент системы разрабатывается так, чтобы обеспечить системе достижение цели с максимальной эффективностью);
- строится иерархия моделей исходя из иерархического характера системы;
- обеспечивается совместное рассмотрение структуры системы и ее функций.
При проектировании сложных технических систем практически невозможно полное описание объекта в рамках одной математической модели - требуется структурирование модели, что позволяет распределять работы по проектированию между отдельными группами исполнителей.
Декомпозиция процесса и объекта проектирования предполагает блочно-иерархический подход к проектированию - переход от исходной обобщенной модели системы к иерархии детальных моделей.
Соответственно иерархии объектов проектирования строится и иерархия их моделей. Получение моделей процедура неформализованная - для каждого из элементов системы разрабатываются несколько моделей, описывающих различные его свойства. При различных исследованиях используются различные сочетания моделей.
Пример: колесо автомобиля. Необходимы отдельные модели для описания его состава, формы, тяговых, упругих, амортизирующих свойств, свойств, определяющих его грузоподъемность, влияние на управляемость и устойчивость движения и т.д.
Проектируемая система выступает, с одной стороны, как часть системы более высокого уровня, с другой – как система для объектов более низкого уровня (подсистем).
Независимо от разбиения конкретной сложной системы на подсистемы при проектировании каждой из них необходимо выполнять внешнее проектирование (создание концепции системы - макропроектирование) и внутреннее проектирование (детальное описание системы - микропроектирование). Так как на этих стадиях разработчик преследует различные цели, то и используемые при этом методы и средства моделирования могут существенно отличаться.
При формировании концепции (структурное проектирование) создается единая укрупненная модель всей системы, целью которой является приближенная сравнительная оценка эффективности альтернативных вариантов концепций (структуры и состава основных компонентов) для выбора наилучшей (нескольких). При этом игнорируется детальная структура системы и анализируется только общее поведение системы как единого целого, оцениваются ее интегративные характеристики и взаимодействие ее с внешней средой.
При детальном проектировании разрабатываются модели с целью создания эффективных подсистем. Причем используемые методы и средства моделирования зависят от того, какие конкретно обеспечивающие подсистемы разрабатываются: информационные, математические, технические, программные и т. д.
Модель системы на этапе внешнего проектирования создается по результатам выполнения следующих системных процедур.
 |
В модели устанавливаются функциональные зависимости, определяющие поведение системы - соотношения между параметрами системы, внешней среды и критериями эффективности для системы в целом и каждого из ее основных компонентов.
В состав системы входят только те компоненты, параметры которых признаны определяющими. Исследуется влияние изменения параметров системы и среды на эффективность (анализ чувствительности).
К числу укрупненных характеристик относятся: границы системы, тип структуры, характер взаимосвязей "вход – выход", особенности функционирования, особенности протекающих процессов, особенности жизненного цикла системы.
Как и весь процесс проектирования, построение моделей имеет циклический итеративный, спиралевидный характер с последовательным расширением понимания системы на каждом шаге с постепенным углублением исследований и пониманием системы, ее сущности, условий функционирования и эффективности.
Основное требование к модели этапа внешнего проектирования - модель не только должна адекватно отражать явления и процессы, но должна быть удобной для использования.
Основным здесь выступает принятая степень упрощения (при разработке матмоделей, выборе состава оптимизируемых параметров системы, определении ограничений) адекватная поставленной задаче - теория упрощений как основа теории систем к настоящему времени не сложилась - все определяет опыт и интуиция проектанта.
Исследование системы происходит с использованием математических моделей с соответствующей степенью упрощенности, с постепенным углублением и уточнением модели, декомпозицией ее на частные модели для конкретных исследований, композицией в общую и т.д.
Сложную систему чаще всего невозможно полностью и детально представить. Возникает проблема компромисса между простотой описания и необходимостью учета многочисленных и разноплановых характеристик системы.
Система любой степени сложности рассматривается, как целостная и организованная, состоящая из отдельных взаимосвязанных элементов, во взаимодействии с внешней средой, находящейся в непрерывном развитии. При этом рассматривается весь комплекс условий функционирования системы во внешней среде – технических, политических, социальных.
В основе общей методологии – сочетание методов анализа и синтеза. Синтез заключается в создании описания объекта, анализ – в определении свойств объекта по его описанию, т.е. при синтезе формируются, а при анализе оцениваются проекты объектов.
Ясно, что не существует универсального метода проектирования любой сложной системы: проектирование сложной системы отнюдь не сводится к слепому следованию некоему набору рецептов.
Процесс проектирования можно представить как последовательное сжатие множества конкурирующих вариантов системы, исходная сложная задача заменяется на последовательность простых. Соответствующие процедуры последовательного анализа вариантов интерпретируются как процесс последовательного снятия неопределенностей.
Процесс проектирования организовывается как многоуровневый процесс переработки информации для принятия проектного решения.
Ключевой проблемой при этом является координация принимаемых проектных решений отдельных задач проектирования. На практике решение этой проблемы основывается на реализации итерационного процесса последовательного согласования проектных решений. Это решается разработкой специальной технологии проектирования.
Если решение задач высоких иерархических уровней предшествует решению задач более низких иерархических уровней, то проектирование называют нисходящим. Если раньше выполняются этапы, связанные с низшими иерархическими уровнями, проектирование называют восходящим.
У каждого из этих двух видов проектирования имеются преимущества и недостатки. При нисходящем проектировании система разрабатывается в условиях, когда ее элементы еще не определены, и, следовательно, сведения о ее возможностях носят предположительный характер. При восходящем проектировании, наоборот, элементы проектируются раньше системы, и, следовательно, предположительный характер имеют требования к элементам.
Принятие оптимального решения обеспечивается последовательным приближением при чередующемся выполнении обоих видов проектирования, что обуславливает итерационный циклический характер процесса проектирования.
Часто этапы проектирования трудно четко разграничить: может проходить параллельное выполнение некоторых этапов и неоднократное повторение пройденных этапов итеративным путем. Например, на каждом этапе может потребоваться уточнение как общей постановки задачи, так и частных.
Любой процесс проектирования имеет свою стратегию проектирования, логическую схему построения проекта и технологию проектирования.
Стратегия проектирования предполагает поиск и определение типов последовательности действий, методов и алгоритмов для решения проектной задачи.
В общем случае стратегии проектирования могут быть линейными, циклическими, разветвленными, адаптивными, смешанными.
При линейной стратегии проектные операции выполняются последовательно. Циклическая стратегия предполагает возможность повторения предыдущей проектной операции в зависимости от результатов предыдущей. При разветвленной стратегии в зависимости от исхода предыдущей проектной операции можно подключать исполнителей для работы на параллельных операциях, при адаптивной стратегии выбор каждого последующего действия зависит от результатов, полученных на предыдущей операции.
Процесс проектирования можно представить как последовательный процесс принятия решений в условиях неопределенностей. Отдаленность этапа непосредственного применения, нечеткое задание стратегий применения приводят к неопределенности будущих условий применения и соответственно характеристик создаваемой системы. Принятые на каждом цикле решения уменьшают степень неопределенности на каждом последующем этапе, что в свою очередь приводит к необходимости последовательного уточнения и детализации проектных решений.
В процессе анализа исследуются:
- необходимость и достаточность всех функций для решения задач системы;
- порядок выполнения функций и согласование всех входов и выходов;
- работоспособность подсистем и системы в целом в различных условиях функционирования;
- сроки разработки проекта и предполагаемые затраты на разработку проекта и эксплуатацию системы.
В результате анализа уточняются математические модели подсистем опорного варианта системы, на основании которых строится упрощенная математическая модель системы в целом. С помощью новой математической модели вновь решаются задачи синтеза и уточняются варианты структурно-функциональных схем системы, для каждого из которых затем снова решаются задачи анализа, и так до тех пор, пока не будет найден приемлемый вариант системы (определен облик системы).
Модель может быть сосредоточена на функциях системы (функциональная модель) или на ее объектах (модели данных).
Функциональная модель выделяет события в системе, представляет с требуемой степенью детализации систему функций, которые в свою очередь отражают свои взаимоотношения через объекты системы.
Модели данных выделяют объекты системы, которые связывают функции между собой и с их окружением и представляют собой подробное описание объектов системы, связанных системными функциями.
Значительная неопределенность информации на предварительных этапах проектирования приводит к рассмотрению «грубых», обобщенных параметров и многовариантных проектных решений – параллельной разработке нескольких вариантов системы. Сужение области неопределенности по мере выполнения проекта позволяет перейти к более детальному рассмотрению характеристик и отказаться от разработки параллельных вариантов.
Специальная методология определяет проектные действия для конкретных типов систем на определенном этапе проектирования – основные типовые направления работ.
Методы специальной методологии – это множество методов решения проектных задач, возникающих при проектировании системы.
Специальная методология проектирования предполагает рациональное разделение процесса проектирования на неформализованные (поиск альтернатив, конструирование, принятие решений) и формализованные (проектные и поверочные расчеты) задачи, выделение эмпирических задач (физическое моделирование). Проектанту предоставляются различные средства и методы решения этих задач.
Системы создаются для решения той или иной проблемы, выполнения тех или иных потребностей – решения этих задач определяют цель функционирования системы.
Первая, начальная задача проектирования – формулировка проблемы, задачи которой призвана решать проектируемая система, и выявление функциональных свойств системы, которые позволят решить возникшую проблему.
Схема формулировки проблемы и функциональных свойств системы:
- выделение системы из внешней среды и рассмотрение ее как элемента системы более высокого уровня;
- анализ задач, решаемых существующими системами;
- анализ изменения условий функционирования системы (изменение целей, условий внешней среды);
- формирование новых задач и функций системы.
Схема формирования концептуального облика объекта (системы)
Концепция системы - укрупненная структура системы, основные функции системы и подсистем.
Цель системы – желаемый результат функционирования системы, ее назначение исходя из решения проблемы системы более высокого уровня, - что нужно сделать для снятия проблемы.
Эффективность – свойство системы выполнить поставленную цель.
Критерии эффективности – те конкретные свойства системы (признаки), по которым оценивается эффективность.
Показатели эффективности – характеристики свойств системы, количественно выражающие степень выполнения поставленной задачи - численные значения критериев эффективности.
Задачи системы – действия (функции) системы, обеспечивающие выполнение цели.
Основные проектные параметры - параметры системы, которые непосредственно обеспечивают эффективность системы.
Схема формирования концепции:
- определение потребностей в системе на основании анализа внешней среды и возможных условий применения системы;
- формулировка цели и требований к системе;
- формулировка основных функций системы, обеспечивающих выполнение поставленной цели;
- определение возможных путей создания системы (формирование функциональной структуры системы и основных ее подсистем).
В структуре системы учитываются только основные элементы, критичные при определении соответствия системы поставленным целям и при оценке эффективности системы.
Структура формируется на основании сравнительного анализа альтернативных вариантов системы, обеспечивающих решение проблемы с учетом внешней среды и неопределенностей будущего функционирования.
Исходя из сформулированных функций системы определяются основные требования к системе в результате выполнения следующих основных системных процедур: формирование понятия эффективности системы (цели, критерии, показатели эффективности), анализ внешней среды и условий функционирования системы, формирование требований к системе.
На основании выбранной концепции системы формируется ее технический облик –определяется перечень задач системы, ее структура и основные характеристики функциональных подсистем.
Типовые проектные процедуры формирования облика системы
Облик системы – структура и основные характеристики системы и основных функциональных подсистем, обеспечивающие выполнение цели, поставленной системой более высокого уровня.
I. Формулировка потребностей в системе.
1.1. Анализ целей и задач, решаемых существующими системами, анализ условий их применения, определение потребностей в модернизации существующей или в создании новой системы.
1.2. Выделение системы из внешней среды и рассмотрение ее как элемента системы более высокого уровня.
II Формирование модели цели (понятия эффективности) системы.
2.1. Определение основных целей, назначения и задач системы:
- формулировка цели системы (иерархии целей) исходя из решения проблемы (задач) системы более высокого уровня;
- определение основных функций системы, обеспечивающих выполнение поставленной задач;
- определение особых условий и ограничений (стоимость, сроки и т.д.).
2.2. Формирование основных требований к системе:
- функциональные требования (к результатам выполнения основных операций);
- эксплуатационные требования.
2.3. Формирование состава критериев и показателей эффективности.
III. Анализ внешней среды и условий функционирования системы, прогнозы на весь период жизненного цикла системы.
3.1. Построение модели внешней среды:
- выявление определяющих параметров внешней среды: объекты функционирования (обслуживания), на которые направлены действия системы, природное окружение, состояние технологий на различных стадиях создания системы, экономическая осуществимость системы;
- анализ политической и экономической обстановки, человеческого фактора, возможных военных аспектов;
- анализ неопределенностей внешней среды и оценка их достоверности, выделение стохастических и нестохастических составляющих.
3.2. Анализ условий функционирования системы:
- прогноз условий функционирования и формирование возможных сценариев применения системы в различных условиях внешней среды;
- анализ неопределенностей функционирования системы, оценка их достоверностей, определение путей уменьшения неопределенностей;
- формирование ограничений на применение системы.
3.3. Формирование основных функциональных и эксплуатационных требований к системе.
IV. Формирование облика системы
4.1. Формирование множества альтернативных вариантов системы, для каждого варианта:
- определение укрупненной структуры, основных функций системы и подсистем, определение состава основных параметров системы;
- разработка математических моделей системы и подсистем (установление зависимостей между основными проектными параметрами и показателями эффективности);
4.2. Выбор рациональных значений основных параметров системы в целом и ее подсистем для каждого альтернативного варианта системы; сравнительный анализ альтернативных вариантов системы.
4.3 Определение технических путей создания системы.
Оценка затрат на создание системы.
Определение путей развития системы.
4.4 Возможность адаптации системы к изменениям внешней среды в течение жизненного цикла системы.
V. Анализ инвестиционной привлекательности системы.
9.3 Эффективность системы
Понятие эффективности системы
Проектные параметры системы - изменяемые в процессе проектирования характеристики, описывающие облик системы.
Основные проектные параметры - те изменяемые параметры системы, которые непосредственно обеспечивают эффективность системы (формируются в процессе проектирования).
Эффективность – свойство системы выполнить поставленную задачу.
Критерии эффективности – те конкретные свойства системы (признаки), по которым оценивается эффективность (при сравнительной оценке вариантов, выборе наилучшего решения…).
Показатели эффективности – характеристики, количественно выражающие степень выполнения поставленной задачи и позволяющие судить об эффективности системы - численные значения критериев эффективности.
Иногда, когда отсутствуют естественные числовые характеристики, вводятся искусственные оценки типа баллов, которые проставляются экспертами.
Эффективность как свойство системы проявляется в системе более высокого уровня, которая для решения своих задач затрачивает определенные ресурсы (оборудование, материалы, энергию) на создание и эксплуатацию системы нижнего уровня. Эти затраты ресурсов системы более высокого уровня являются основанием для выбора наилучшей системы нижнего уровня.
Свойства системы, обеспечивающие выполнение цели, отражают эффективность системы (качество выполнения поставленной цели) и соответствующие этой цели затраты. Поэтому, применительно к задачам проектирования, критерий должен соотносить цель со свойствами системы, обеспечивающими ее выполнение.
Эффективность системы определяется для всего жизненного цикла системы с учетом ее развития (модернизации). Это влияет на выбор основных проектных параметров системы – система, параметры которой позволят провести модернизацию с наименьшими затратами является более эффективной.
Наиболее общий показатель для оценки затрат ресурсов – стоимость создания и эксплуатации системы.
Пример. Космическая система наблюдения Земли по отношению к отраслям хозяйства, социальным системам является системой нижнего уровня и ее эффективность оценивается по тому, как, какими затратами эта система обеспечивает выполнение поставленных перед ней целей системы более высокого уровня.
Между показателями и критериями эффективности нет четкого разделения (одни могут переходить в другие). Например - взаимосвязь эффективности по каким-то показателям и стоимости (бессмысленно требовать максимальную эффективность при минимальной стоимости).
Два эквивалентных варианта взаимосвязи эффективности и стоимости: затраченные ресурсы должны обеспечить наивысшую эффективность системы или требуемая эффективность должна быть обеспечена при минимальных затратах.
Экономическая эффективность системы – экономический результат (доход), приносимый системе верхнего уровня системой нижнего уровня, соотнесенный с суммарными затратами ресурсов системы верхнего уровня на создание, эксплуатацию и использование результатов функционирования системы нижнего уровня. Экономическая эффективность оценивается двумя показателями – доходом и затратами ресурсов.
Показателями эффективности могут быть:
- максимальный доход при заданном (в виде ограничения) ресурсе;
- минимальные затраты при заданном (в виде ограничения) доходе;
- максимальный доход на единицу затраченного ресурса.
Возможны показатели, использующие разность между доходом и затраченным ресурсом – максимальная прибыль, максимальная рентабельность (отношение прибыли к затратам).
Формирование модели цели системы
Выбор цели – первая, исключительно важная составляющая постановки задачи по выбору концепции системы. Цель, поставленная перед системой, непосредственно влияет на облик создаваемой системы, ее состав, структуру и характеристики.
Для терминов "цель, задача, эффективность, критерий, показатель эффективности" нет устоявшихся универсальных определений. Имеются только сложившиеся общие представления.
Цель системы – желаемый результат функционирования системы, ее назначение, определяемое заказчиком системы (основные решаемые задачи).
Цель определяется поставленной проблемой материального, экономического, социального, оборонного характера (повышение благосостояния, повышение эффективности производства, повышение обороноспособности …) – что надо сделать для снятия проблемы. Выбранная цель оценивается исходя из необходимых для ее достижения средств.
В общем случае цель указывает общее направление, в котором необходимо двигаться для достижения лучшего результата. При этом поставленная цель не должна быть противоречива. Цели «Сократить затраты и улучшить качество обслуживания» в общем случае могут быть противоречивы.
Модель цели – описание потребности в системе, назначения системы и требований к ней (на естественном языке).
Описание назначения состоит из трех составляющих:
- наименование действий системы, которые приводят к желаемому результату (например, наблюдение авиационными средствами, наблюдение Земли из космоса), характеристики действий (например, периодичность, время наблюдения);
- указание условий функционирования во внешней среде или объекта, на который воздействует система – объекта обслуживания (например, обнаружение пожаров, определение параметров атмосферы для решения какой-то задачи);
- указание особых условий и ограничений, при которых выполняется действие (поддержание структуры системы, срок эксплуатации, стоимость создания и эксплуатации).
Определение цели – сложный неформализуемый процесс, который требует проявления интуиции и творчества, выполнения качественного и количественного анализа возможных целей, корректировки, уточнения цели в процессе проектирования. Некоторые типовые работы, предшествующие определению целей: обзор проблемы, аналитические исследования подобных целей в других отраслях (например, при составлении какой либо программы развития региона, отрасли – проанализировать цели в подобных программах).
Описание цели формулируется в техническом задании (описание потребности в системе, назначения системы и требований к ней) в результате анализа политической и экономической обстановки, исследования целесообразных сфер и способов применения систем, возможностей реализации и затрат на создание системы, возможностей военного применения, стратегии и тактики применения.
Итеративный процесс формирования цели заканчивается одновременно с окончанием синтеза системы, и сущность его может быть охарактеризована термином «синтез цели системы».
Основные положения синтеза цели (неформализуемые, на интуитивном уровне).
Необходимо найти правильное соотношение между всеобъемлющей и узкой целью. Всеобъемлющая цель не даст возможности четко сформулировать задание на разработку, узкая цель не даст возможности четко определить характеристики системы.
Всеобъемлющая цель – создать систему наблюдения Земли, узкая цель – создать систему наблюдения Земли с какой-то одной выбранной характеристикой (например, оперативностью доставки данных - нет возможности определить остальные характеристики – аппаратуру, высоту орбиты…).
Всеобъемлющая цель – создать самолет, узкая цель – создать самолет с самой большой дальностью полета (нет возможности определить остальные характеристики – грузоподъемность…).
Цель нельзя заменять средствами выполнения цели.
Строительство больницы – не цель улучшения медицинского обслуживания населения района, а средство. Возможно, улучшение медицинского обслуживания можно достичь другими, более эффективными средствами, чем строительство больницы.
Смешение целей.
Операция прошла успешно, но пациент умер. Внешне красивое здание может быть непригодно для использования из-за внутренней планировки.
Смешение целей могут быть причинами экологических бедствий (Байкал, поворот рек).
Изменение цели со временем.
Изменение цели со временем может происходить не только по форме, в силу все большей конкретизации действительных целей, но и по содержанию – вследствие изменения объективных условий и/или субъективных установок, влияющих на выбор цели. Сроки старения целей различны и зависят от многих причин. Цели более высоких уровней долговечнее. В социальных системах сроки достижения целей высших уровней часто формулируются как интересы будущих поколений, сроки целей нижних уровней связаны с действиями ближайшего будущего.
Иерархия целей соответствует иерархической структуре системы. Благодаря согласованности и взаимной подчиненности своих целей, все подсистемы работают целенаправленно для достижения общей цели системы. Однако это не простое сложение целей – реализация каждой из подцелей приводит в целом к достижению качественно новой цели высшего уровня (интегративное свойство системы). Каждая цель характеризуется критерием эффективности.
Графическое представление целей – дерево целей. Нижний уровень – возможность представления цели в численном виде.
Цели нижнего уровня представляют собой неизбыточный набор, конкретизирующий исходную общую цель. Более мелкое деление может привести к потере набора целей свойства неизбыточности, поскольку влияние каждой мелкой цели на общую цель может оказаться пренебрежительно малым.
Схема формирования цели как составной части синтеза системы: составление сценариев функционирования системы, построение дерева целей, выявление взаимосвязей между целями и задачами одного уровня и разных уровней.
На основании целей системы формируются требования и ограничения к характеристикам системы.
Предварительные требования и ограничения к системе подвергаются детальному анализу: с учетом стоимости, с учетом скрытых факторов. Например, может предусматриваться использование компонентов системы, которые выпускаются или будут разработаны внутри страны, даже если в других странах такие компоненты дешевле. В этом случае приходится тратить больше средств вследствие политического ограничения (использование проекта для развития национальной экономики). Эти требования и ограничения уточняются и детализируются по мере расширения наших представлений о системе в ходе проектирования.
Среди требований выделяются основные, "ведущие требования", в наибольшей степени определяющие эффективность системы. Это функциональные и эксплуатационные требования, условия и ограничения.
Функциональные требования – это требования к результатам выполнения целевых операций, определяющих эффективность системы, и требования, обусловленные характеристиками объектов, на которые направлены действия системы (объектов обслуживания).
Эксплуатационные требования – это требования к операциям, обусловленные характеристиками объектов обслуживания, и требования к технической готовности системы (требования к операциям по поддержанию структуры системы – требования к безотказной работе компонентов системы, требования к восстановлению или замене отказавших компонентов системы).
Требования, обусловленные особыми условиями и ограничениями: требования к сроку службы системы, к стоимости создания и эксплуатации, ограничения по основным факторам внешней среды (в том числе политических, социальных).
Под сроком службы понимается календарное время эксплуатации до наступления предельного состояния системы, обусловленное моральным (моральное устаревание), техническим (невосстанавливаемость), экономическим (затраты на ремонт) факторами. Срок службы зависит от затрат на создание системы.
В структуре системы учитываются только основные элементы, критичные при определении соответствия системы поставленным целям и при оценке эффективности системы.
Задача выбора оптимального облика системы решается при декомпозиции ее на две задачи: структурную и параметрическую оптимизации (синтез и анализ системы).
Выбор критериев и показателей эффективности
Выполнение заданной цели неизбежно связано с затратами материальных, энергетических и других ресурсов, необходимых для создания и эксплуатации системы. Свойства системы, обеспечивающие выполнение цели, отражают эффективность системы (качество выполнения поставленной цели) и соответствующие этой цели затраты. Поэтому, применительно к задачам проектирования, критерий должен соотносить цель со свойствами системы, обеспечивающими ее выполнение.
Различают общий критерий эффективности – признак, по которому оценивают эффективность всей системы, и локальный критерий – признак, по которому оценивают выполнение конкретной задачи подсистемой. Чем подробнее иерархия целей, тем легче установить количественные значения критериев.
Основные принципы выбора критериев эффективности:
- критерий должен быть согласованным с моделью цели – необходимость строгого соответствия между целью, поставленной перед системой, и критерием эффективности (трудности выбора критериев чаще всего встречаются при нечетко поставленной задаче),
- неизбыточность - критерий должен соответствовать масштабу исследований,
- максимально полный учет всех факторов, определяющих эффективность системы.
- минимальная размерность набора критериев
- непротиворечивость частных критериев общему.
Критерии-заместители – критерии, которые косвенно характеризуют цель, но не являются средством непосредственного измерения для этой цели (комфортность пассажиров).
Например, цель службы скорой помощи – «доставка больного в больницу в наилучшем состоянии, возможном при данных обстоятельствах». Поскольку эта цель не имеет очевидного критерия, можно принять три критерия-заместителя: «время реагирования», "объем помощи на месте", «время доставки в больницу».
Многие критерии настолько широко и привычно используются, что уже не считаются критериями-заместителями. Например, «прибыль» – критерий-заместитель критерия «благосостояние» (но не все можно измерить деньгами, например, условия работы в коллективе). Или «доля участия в рынке» – заместитель критериев престиж, получение будущих прибылей.
Основные требования к показателям эффективности:
- должен быть простым и наглядным, иметь ясный физический смысл, позволяющий четко интерпретировать результаты исследований,
- обеспечивать вычисление оценки соответствующего требования к системе,
- быть чувствительным к проектным параметрам вариантов системы.
В структуре системы учитываются только основные элементы, критичные при определении соответствия системы поставленным целям и при оценке эффективности системы.
Задача выбора оптимального облика системы решается при декомпозиции ее на две задачи: структурную и параметрическую оптимизации (синтез и анализ системы).
Проблемы многокритериальности
При проектировании может оказаться необходимым анализировать несколько критериев: набор количественно измеримых целей на нижнем уровне иерархии целей системы не сводится к одной цели; каждая цель не обязательно характеризуется единственным критерием.
Если критерии, характеризующие систему, являются противоречивыми – возникает задача многокритериального выбора (в условиях, как определенности, так и неопределенности).
Например, необходимо найти рациональный вариант облика системы, качество которой оценивается по критериям: стоимость, надежность, время выполнения задачи.
Основные принципиальные трудности решения многокритериальных задач связаны с выбором принципа оптимальности (определяющего правила выбора рационального решения) и с выбором принципа учета приоритета, позволяющего отдавать предпочтение более важным критериям.
В общем случае задача многокритериальной оптимизации формулируется как задача одновременной оптимизации некоторой совокупности показателей. Строго математическая задача в такой постановке смысла не имеет, так оптимумы отдельных показателей достигаются при разных значениях критериев: необходимо применение математических методов принятия решений совместно с методами оптимизации. Как правило, критерии противоречивы: повысить значение одного удается только за счет некоторого снижения значения другого.
Здесь вступают в противоречие одни из основных свойств системы – универсальность и специализация. Эти свойства являются проявлением противоположных тенденций: с одной стороны – стремление сократить количество разнотипных систем с целью снижения затрат на их создание и эксплуатацию, с другой – повышение эффективности выполнения каждого отдельного задания. В процессе проектирования определяется рациональное сочетание этих свойств.
Наилучшая эффективность системы для одной из целей (одного показателя эффективности) приводит к уменьшению эффективности для других целей (показателей). Такое уменьшение эффективности характеризует уровень универсальности системы при выполнении отдельных целей и с расширением области целевого применения увеличивается, достигая недопустимо больших значений на границе этой области.
Естественным путем повышения целевой эффективности системы является использование системы не на всей возможной, а на некоторой более узкой области применения. Это характеризует другое важное свойство системы – специализацию. Предельный случай, "абсолютная специализация" – сужение до одного наиболее эффективно выполняемого задания.
Решение многокритериальных задач требует проведения модификаций понятия оптимальности, применение различных способов свертки критериев, многовариантной оптимизации в широком диапазоне изменений исходных требований и ограничений, оценки чувствительности полученных решений к их изменениям, выделение паретовских множеств с их последующим сужением за счет дополнительной информации, и т.д.
Основные принципиальные трудности решения многокритериальных задач связаны с выбором принципа оптимальности, определяющего правила выбора рационального решения, а также с выбором принципа учета приоритета, позволяющего отдавать предпочтение более важным критериям.
Основные классы многокритериальных задач принятия решений.
Задачи выбора решения на множестве целей. Имеется несколько целей, каждая из которых должна быть учтена при выборе рационального решения. Здесь качество решения необходимо оценивать с разумных точек зрения по различным составляющим качества, которые и образуют векторный критерий эффективности. Все частные критерии оптимальности противоречивы и имеют различные масштабы измерения.
Пример: найти рациональный вариант космического аппарата, качество которого оценивается по критериям стоимости, массы полезной нагрузки, надежности, времени функционирования. При проектировании каждый КА оценивается векторным критерием.
Задачи оптимизации на множестве объектов. Имеется несколько объектов, качество функционирования каждого из которых оценивается самостоятельным критерием. Тогда качество функционирования всей совокупности объектов системы оценивается по векторному критерию.
Пример: найти оптимальный вариант системы разнотипных носителей для создания орбитальной группировки. Каждый тип носителя характеризуется частным критерием оптимальности, например, стоимостью вывода единицы полезного груза.
Задачи оптимизации на множестве условий. Заданы варианты условий, в которых предстоит функционировать системе, причем, качество функционирования существенно зависит от условий. Качество функционирования системы для каждого варианта условий оценивается частным критерием, а для всего множества – векторным. Если условия задаются не дискретно, а виде сплошного спектра, вектор эффективности может быть бесконечномерным.
Задачи эффективности в динамике или на множестве этапов. Качество решения оценивается для каждого момента времени (этапа) частным критерием, для всего заданного периода – векторным критерием.
Пример: оптимальное движение по траектории, которая разбита на этапы. Качество прохождения каждого участка оценивается по своему критерию, качество прохождения траектории в целом – по векторному критерию.
Задачи оптимизации на множестве вариантов постановок задачи. Здесь неопределенность, связанная с неполнотой постановки задачи или неопределенность формализации подменяется неопределенностью, связанной с понятием многокритериальности. В действительности реальна лишь одна из компонент векторного критерия, но неизвестно, какая из них конкретно.
Существующие способы многокритериальной оптимизации можно разбить на две группы: введение дополнительных гипотез, позволяющих свести задачу многокритериальной оптимизации к однокритериальной (свертывание показателей), и сокращение множества вариантов решений методами неформального анализа (задачи принятия решений).
Способы сведения многокритериальной задачи к однокритериальной.
В исследовании операций выработаны некоторые способы решения многокритериальных задач, и выбор конкретного способа зависит от постановки задачи и дополнительных гипотез. Это:
- сведение многокритерильной задачи к однокритериальной (свертка критериев введением весовых коэффициентов, обобщенных показателей или ограничений – "перенос произвола из одной инстанции в другую");
- многократное решение прямой задачи оценки эффективности;
- выделение паретовских множеств (принцип отбора рациональных решений);
- сокращение множества вариантов решений методами неформального анализа (задачи принятия решений) и др.
Объединение нескольких критериев в один суперкритерий. Пример – бальная система оценки качества. Упорядочение частных критериев с помощью коэффициентов отражает относительный вклад каждого из них в обобщающий критерий. Упорядочение точек в многомерном пространстве в принципе не может быть однозначным и полностью определяется видом упорядочивающей функции, роль которой играет суперкритерий (обобщенный критерий). Идея такого упорядочивания в многомерном пространстве заложена в некоторых бальных системах.
Наиболее распространенным на практике является переход от нескольких показателей к одной целевой функции – свертывание показателей на основе использования дополнительной объективной информации (об объективных свойствах системы) и субъективной информации (введение весовых коэффициентов об относительной важность показателей эффективности). Дополнительную информацию об объективных свойствах системы можно получить при рассмотрении эффективности системы более высокого уровня.
При свертывании частные критерии в большинстве случаев неравнозначны между собой. Здесь возможно выделение основного, главного критерия, а остальные критерии рассматриваются как сопутствующие, или задаются в виде ограничений, причем, даже не в виде жестких, а в виде неравенств (например, только в виде верхних или нижних границ).
Если различия между значимостью критериев не слишком сильные, может быть применен метод уступок. В этом случае частные критерии упорядочиваются в порядке убывания их важности. Ищется альтернатива, по первому, наиболее важному критерию. Затем определяется уступка, т.е. величина, на которую мы согласны уменьшить достигнутое значение самого важного критерия, чтобы за счет уступки попытаться увеличить, насколько возможно, значение следующего по важности критерия и т.д.
При многократном решении задач оптимизации для каждого из показателей и сравнении результатов друг с другом, в результате анализа множества альтернатив происходит исключение заведомо неоптимальных вариантов решений, и может оказаться (крайне редкий случай), что существует одна доминирующая альтернатива, наилучшая для всех показателей. На практике альтернатива, улучшающая один из показателей, часто обуславливает ухудшение других показателей эффективности. При таком подходе среди множества альтернатив выделяется подмножество Парето-оптимальных альтернатив, обладающее следующим свойством: любая альтернатива этого подмножества лучше какой-либо другой или нескольких других из исходного множества по одному показателю, но хуже по другим. Парето-оптимальные решения нельзя одновременно улучшить по всем частным критериям эффективности. не ухудшив при этом значения хотя бы одного из показателей.
Формализуемый способ многокритериального выбора состоит в отказе от выделения единственной "наилучшей" альтернативы и соглашении о том, что предпочтение одной альтернативе перед другой можно отдавать только если первая по всем критериям лучше второй. Если же предпочтение хотя бы по одному критерию расходится с предпочтением по другому, то такие альтернативы признаются несравнимыми. В результате попарного сравнения все худшие по всем критериям альтернативы отбрасываются, а все оставшиеся несравнимые между собой (недоминируемые) принимаются. Если все максимально достижимые значения частных критериев не относятся к одной альтернативе, то принятые альтернативы образуют множество Парето и выбор на этом заканчивается. При необходимости выбора одной альтернативы вводятся новые, добавочные критерии и ограничения, привлекаются эксперты, бросается жребий.
9.4 Технология проектирования
Проектирование ведется в соответствии с определенным планом – логической схемой проектирования.
Логическая схема проектирования в общем случае представляет собой иерархическую структуру, включающую декомпозицию проектируемой системы на подсистемы и декомпозицию процесса проектирования на уровни. При этом должно быть обеспечено исследование влияния принятых частных решений на проведение сложной системы в целом.
Логическая схема проектирования разрабатывается на основании принятой стратегии проектирования и устанавливает маршрут проектирования объекта – последовательность этапов и (или) проектных процедур
Реализуется логическая схема на основании опробованной последовательности действий – технологии проектирования.
Для каждого конкретного типа системы и решаемой проектной задачи на основе общих (системный подход к проектированию) и специальных методологических принципов разрабатываются логическая схема проектирования и специальная технология проектирования, учитывающие специфику решаемой задачи, традиционно используемые методы и методики проектирования.
Элементами технологии проектирования являются проектные процедуры как составные части этапа проектирования и проектные операции как составные части проектной процедуры.
Проектная процедура предполагает выполнение формализованной совокупности действий (алгоритм проектирования[2]), в результате которых принимается проектное решение.
Каждой проектной процедуре соответствует некоторая задача проектирования, решаемая в рамках данной процедуры.
В обобщенном виде проектная процедура характеризуется входом (исходные данные процедуры), выходной информацией, в том числе показатели эффективности выполнения системой своих задач, множеством моделей объекта проектной процедуры, множеством методов решения проектной задачи.
Выполнение проектной процедуры заканчивается получением проектного решения.
Проектная операция - более мелкая составная часть процесса проектирования, входящая в состав проектной процедуры.
Примеры проектных процедур: расчет параметров какого-либо узла, оформление чертежа узла, выбор конструкции.
Примеры проектных операций: решение системы уравнений, описывающих функционирование какого-либо узла, вычерчивание типового графического изображения элемента узла.
Выполнение проектных операций и процедур в процессе проектирования основано на применении математических моделей, отражающих свойства объекта важные для конкретных целей проектирования на каждом этапе.
Технология проектирования определяется как совокупность составляющих:
- последовательность проектных процедур и операций, реализующих логическую схему проектирования;
- критериев и правил оценки результатов выполнения проектных операций;
- графических и текстовых средств, используемых для описания результатов проектирования.
Основное содержание технологии - технологические инструкции, описывающие последовательность проектных операций и сами операции, условия, в зависимости от которых выполняется та или иная операция.
Для каждой процедуры и операции проектирования определяются исполнители, методические, программные и технические средства, исходные данные и результат выполнения операции выдается в стандартном представлении (документы, результаты предыдущей операции).
Общие требования к технологиям проектирования:
- поддержка жизненного цикла системы;
- обеспечение гарантированного достижения целей разработки системы с заданным качеством и в установленное время;
- обеспечение возможности выполнения крупных проектов в виде подсистем отдельными проектными группами (т.е. возможность декомпозиции проекта на составные части с последующим их объединением) с координацией ведения общего проекта;
- обеспечение возможности управления конфигурацией проекта, ведения версий проекта и его составляющих;
- поддержка процесса проектирования комплексом согласованных средств, обеспечивающих автоматизацию процессов, выполняемых на всех стадиях жизненного цикла.
Реальное применение любой технологии проектирования, разработки и сопровождения системы в конкретной организации и конкретном проекте основано на ряде стандартов (правил, соглашений), которые должны соблюдаться всеми участниками проекта.
Период развития системы разделяется на два основных этапа: проектирование и ввод системы в эксплуатацию (изготовление опытных образцов, экспериментальная отработка, изготовление системы, опытная эксплуатация системы).
Особенности процесса проектирования определяются типом проекта. Проекты могут классифицироваться по масштабу (малый, средний, крупный проект), по сложности (простой, организационно сложный, технически сложный, ресурсно сложный).
Малые проекты допускают упрощения в процедуре проектирования, формировании команды проекта. Крупные проекты отличаются высокой стоимостью, капиталоемкостью, длительностью реализации.
Проектируемая система выступает, с одной стороны, как часть системы более высокого уровня, с другой – как система для объектов более низкого уровня (подсистем). В соответствии с этим процесс проектирования состоит из двух основных этапов: внешнего проектирования и внутреннего проектирования.
Разработка системы осуществляется в соответствии со стандартами ГОСТ, ЕСКД, ЕСПД, ISO.
Для каждого этапа проектирования вырабатываются некоторые типовые приемы моделирования и общие способы работы с моделями – в зависимости от целей и задач этапа.
Построение математических моделей является основой этапа внешнего проектирования – с помощью математической модели, устанавливающей связь критерия эффективности системы с ее основными проектными параметрами, формируется концепция системы и определяются ее основные проектные параметры, обеспечивающие максимальную эффективность системы.
Исследования с помощью модели на этапе внешнего проектирования:
- влияние внешних воздействий на систему;
-основные процессы в системе при ее функционировании, влияние структуры и характеристик системы на процессы и динамику их изменения;
-возможность и необходимость управления процессами в системе, основные управляющие воздействия, их тип, источник, степень влияния на систему.
В результате циклического итеративного повторения этих исследований выявляется структура системы, ее элементы, связи, значимость каждого из них.
На этапе внешнего проектирования в зависимости от степени новизны определяются задачи проектирования сложных систем (модернизация существующей или создание новой системы для решения новых задач), формируются структура и основные параметры (облик) системы и оценивается эффективность ее применения. На этапе внутреннего проектирования принимаются технические решения по основным элементам системы, их конструкции, параметрам, режимам эксплуатации.
На этапе внешнего проектирования, как правило, генерируется много вариантов системы, проводится их сравнительный анализ с точки зрения соответствия функциональному назначению системы, дается предварительная оценка эффективности вариантов, и определяются наиболее предпочтительные из них. Характеристики и параметры системы рассматриваются укрупнено, оценивается эффективность решения поставленной задачи. Важную роль при этом играет правильный прогноз развития науки и техники.
Основные особенности процесса внешнего проектирования:
- проектируемая система рассматривается как элемент системы более высокого уровня;
- отсутствие многих исходных данных, неопределенность условий применения, требований и ограничений;
- проведение исследований в широком диапазоне изменения параметров, условий применения, требований и ограничений;
- необходимость анализа большого количества вариантов;
- активное участие руководителей, что требует большой оперативности в проектных проработках и наглядного представления результатов.
Процесс согласования технического задания между заказчиком и разработчиком носит итеративный асимтотический характер. В процессе согласования разрешается конфликтная ситуация между желаемым (заказчик) и возможным (разработчик). Как правило, согласование достигается не сразу, а в результате компромисса: требования к системе не столько задаются, сколько вырабатываются в процессе взаимного обучения сторон.
Проектные решения, принятые на этапе внешнего проектирования определяют эффективность системы и весь ход ее дальнейшей разработки системы, ошибки этого этапа практически неисправимы на последующих этапах.
Проектирование отдельных компонентов сложной системы при ее частичной модернизации является традиционной задачей, решаемой каждый раз на новом уровне в соответствии с развитием техники. Существенная модернизация или создание новой системы происходит чаще всего на основе типичных, ранее созданных компонентов системы, модернизированных для решения новых задач.
Особенности современных крупных проектов сложных систем:
-сложность описания (большое количество элементов, функций, процессов, данных и сложные взаимосвязи между ними), требующая тщательного моделирования и анализа данных и процессов;
-наличие совокупности тесно взаимодействующих компонентов (подсистем), имеющих свои локальные задачи и цели функционирования;
Пример информационных систем: наличие традиционных приложений, связанных с обработкой транзакций и решением регламентных задач, и приложений аналитической обработки (поддержки принятия решений), использующих нерегламентированные запросы к данным большого объема.
-необходимость интеграции существующих и вновь разрабатываемых компонентов системы;
-разобщенность и разнородностью отдельных групп разработчиков компонентов системы по уровню квалификации и сложившимся традициям использования тех или иных средств проектирования;
-неопределенность внешней среды и условий функционирования;
Пример информационных систем: функционирование в неоднородной среде на нескольких аппаратных платформах.
-существенная временная протяженность процесса проектирования.
9.5 Принятие решений в проектировании
Процесс проектирования – многоэтапная итеративная последовательность действий, по результатам которых проектантом (или группой) принимаются проектные решения.
Основные фазы работ при принятии решений – постановка задачи, анализ информационной ситуации, выбор метода и принятие решения, анализ результата.
Особенность принятия решения в процессе проектирования – интерактивность, т.е. возврат на ранние стадии с целью корректировки модели системы, внесения изменений в постановку задачи и т.п.
Процесс принятия решений можно представить как процесс выбора альтернатив (вариантов действий), в результате которого исходное множество сужается. Сужение множества альтернатив возможно, если имеется способ сравнения альтернатив между собой и определения наиболее предпочтительных.
Принятие решения является действием, придающим проектированию целенаправленность – подчиненность всей деятельности определенной цели или совокупности целей.
Считается, что множество альтернатив и цели, ради которых производится выбор, определены.
Проблема принятия решений нетривиальна, ее математическая постановка во многом зависит от конкретной ситуации.
Множество альтернатив может быть счетным дискретным (конечным или бесконечным), непрерывным.
Оценка альтернативы может осуществляться по одному или нескольким критериям, которые могут иметь количественный или качественный характер.
Режим выбора может быть однократным или повторяющимся, допускаемым обучение на опыте.
Последствия выбора могут быть точно известны – выбор в условиях определенности, иметь вероятностный характер, когда известны вероятности возможных исходов выбора, или иметь неоднозначный исход, не допускающий введения вероятностей – выбор в условиях неопределенности.
Различные сочетания перечисленных вариантов приводят к многообразию задач выбора, которые изучены не в одинаковой степени. Различные постановки приводят к различным методам решения и к привлечению различных теорий (теории оптимизации, вариационного исчисления, математической статистики, исследования операций - математического программирования, теории игр, и т.д.).
Проблема выбора состоит в том, чтобы в исходном множестве найти наилучшие в заданных условиях, т.е. оптимальные альтернативы. Наилучшие – значит известен критерий (критерии) сравнения вариантов, способ сравнения вариантов и нахождения лучшего из них. При этом важно учесть условия, ограничения, так как их изменения могут привести к тому, что наилучшим окажется другой вариант.
Практика проектирования требует осторожного подхода к оптимизации.
Многие задачи проектирования трудно достаточно хорошо формализовать и свести к математическим моделям, позволяющим ставить и решать оптимизационные задачи.
Оптимальные решения часто бывают неустойчивыми. Их сильная чувствительность к незначительным изменениям в условиях задачи, неоднозначность постановки многокритериальных задач могут привести к выбору существенно отличающихся альтернатив.
Критерии характеризуют цель лишь косвенно и всегда приближенно. Критерий не всегда четко может отображать цель - фактически критерий и цель соотносятся между собой как модель и оригинал (количественный критерий является суррогатом цели). Многие цели трудно или даже невозможно количественно описать.
Предположение, что принятые критерии достаточно хорошо отображают поставленную цель, необходимость рассмотрения системы как элемента системы более высокого уровня, приводит к необходимости увязывания критериев подсистем с критериями системы, что часто делает ненужной локальную оптимизацию и достаточно сложной общую оптимизацию.
Ограничения и условия применения имеют не менее важную роль, чем критерии. Задание всех ограничений и условий применения практически нереально – в результате может быть выбран или неоптимальный вариант, или могут быть получены непредвиденные или нежелательные эффекты.
В конечном счете, вопрос стоит не в том, как оптимизировать, а в том, нужно ли вообще оптимизировать, и, если оптимизировать, то что.
Результаты оптимизации следует рассматривать как предварительные, предоставляющие вспомогательные данные для принятия решения о дальнейшем анализе и, возможно, постановке новой задачи оптимизации.
Два типа схемы решения задач – формализованные (формально-логические) и неформализованные (интеллектуально-логические).
Процедура (операция) считается формализованной, если определена и однозначно понимается последовательность элементарных действий по ее реализации. Формализация предполагает возможность многократного повторения процедуры (неуникальность), пригодность для множества исходных данных (вариативность входов), возможность формального представления последовательности действий и фиксации его на каком либо носителе (ЭВМ).
В формализованных задачах выбор схемы решения четко задается проектантом в виде программы.
Неформализованные действия осуществляются с использованием интуиции (неполное осознание аргументов и приемов выбора действия). Примеры неформализованных действий – выбор метода решения, декомпозиция, формирование структуры, анализ результатов и т.п.
Чаще всего в процессе проектирования применяется сочетание формализованных и неформализованных действий с использованием САПР.
В зависимости от степени формализации различаются задачи:
- множество альтернатив определено, принцип выбора формализован, и результаты его применения не зависят от субъективных условий (задача оптимального выбора);
- множество альтернатив определено, но принцип выбора не формализован, и результаты выбора зависят от того, кто и на основе какой информации его делает;
- множество альтернатив не определено (может дополняться и видоизменяться), принцип выбора не формализован (разные субъекты могут выбирать разные альтернативы).
В формализованных задачах выбор схемы решения жестко задается программой, составленной проектантом. Это обычно стандартные операции.
Построение интеллектуально-логических схем решения проектных задач связано с принятием проектных решений, основанных на логическом представлении задачи с использованием формализованных компонентов интеллектуальной деятельности. Это выражается в использовании ряда приемов: организация итеративного решения набора формализованных задач – начальное решение одной или нескольких формализованных задач, экспертный анализ решения, формирование измененных множеств альтернатив и принципов выбора, новое решение набора задач и т.п. до получения удовлетворительного результата.
Практические пути решения не полностью определенных задач состоят в использовании ряда задач с фиксированным, но меняющимся от задачи к задаче множеством альтернатив и фиксированным принципом выбора.
Принцип выбора может допускать участие экспертов, каждый из которых может порождать свое множество альтернатив и принципы выбора. В любом случае основой задачи выбора является сведение ее к множеству формализованных задач и организации их сравнения.
Организация решения предполагает: декомпозицию альтернатив на свойства, удобные для сравнения; ранжирование этих свойств; выбор числовых характеристик свойств (критериев); выбор экспертных процедур для оценки свойств. принятие решения.
К организации принятия решения привлекаются следующие виды специалистов:
Лицо, принимающее решение (ЛПР) – полностью отвечает за решение задачи. ЛПР организовывает решение задачи по этапам и единолично принимает окончательное решение.
Консультанты (помощники) ЛПР. Участвуют в организации решения (с привлечением специалистов по системному анализу), обсуждают результаты (в качестве назначенных ЛПР защитников или оппонентов).
Эксперты – в заданных жестко ограниченных рамках производят оценку, сравнение, ранжирование представленных им на экспертизу отдельных сторон альтернатив.
Специалисты по использованию технических средств (постановка задач на ЭВМ, выбор методов решения задач, организация баз данных), специалисты по системному анализу (организация процедуры принятия решения).
Общий язык, на котором описывается выбор – язык бинарных отношений. Его общность основана на том, что в реальности дать оценку отдельно взятой альтернативе часто затруднительно или невозможно. Однако, если рассматривать ее не в отдельности, а в паре с другой альтернативой, то находятся основания сказать, какая из них наиболее предпочтительна.
Основные предположения при этом сводятся к следующему:
- отдельная альтернатива не оценивается, т.е. критериальная функция не вводится;
- для каждой пары альтернатив некоторым образом можно установить, что одна из них предпочтительнее другой либо они равноценны или несравнимы;
- отношения предпочтения внутри любой пары альтернатив не зависит от остальных альтернатив, предъявленных к выбору.
Выбор в условиях неопределенности
Понятия, не всегда строгие, категории не чисто качественного, но и не чисто количественного характера, проверка предположений с помощью численных расчетов характерны для процесса проектирования. Многие задачи просто "не решаются" на достаточно строгом уровне.
В практике проектирования широко применяются так называемые рациональные рассуждения (нестрогие рассуждения, но обеспечивающие при разумном их применении правильные результаты). Применение рациональных понятий, непосредственно связано с интуицией, здравым смыслом. Качество интуиции зависит от степени изучения данной области знания и личных качеств исследователя.
Рациональность рассуждения может оцениваться по степени достоверности рассуждения, которое может меняться от 0 до 1. Это некоторая субъективная аналогия вероятностной оценки. Трудности в определении численных значений степени достоверности приводят к необходимости прибегать к словам, например, к таким: "довольно правдоподобно" (р = 0.9).
Сложное рациональное рассуждение обычно включает физические соображения, "размытые понятия", ссылки на опыт, интуицию, целесообразность упрощения, а также дедуктивные рассуждения.
Различные рассуждения не равноценны, как по трудности их проведения, так и по вкладу в успех решения задачи. По аналогии с теорией вероятностей - если сложное рассуждение является объединением простых, то наличие среди простых рассуждений достоверного рассуждения не повысит при этом общую степень достоверности. Достоверность рационального рассуждения может быть также повышена, если прибегнуть к коллективному мнению.
Под групповым выбором обычно понимается сведение различных индивидуальных мнений о порядке предпочтения рассматриваемых объектов в единое "коллективное" предпочтение.
Проблема группового выбора – общая проблема "разумного" перехода от заданных "индивидуальных наборов данных" к единому "групповому набору данных".
Индивидуальный набор данных может иметь разную природу: члены коллектива и их "голоса" – модели голосования; эксперты и их оценки – анализ экспертных оценок; потребители и их предпочтения – тория потребительского спроса.
Формы организации экспертиз разнообразны и многочисленны: по способам представления экспертами результатов (анкеты, таблицы, интервью, аналитический текст), по взаимодействию между экспертами (свободное, регламентированное, недопустимое), по способам оценки мнений экспертов (голосование, методы группового выбора).
Модели голосования. Альтернатива, получившая наибольшее число голосов, считается принятой. Такое решение не является критерием истины – только дальнейшая практика покажет это. Здесь также трудности с постановкой задачи, определением критерия, определением правил голосования: простое большинство (51%), подавляющее большинство (75%), абсолютное большинство (близко 100%).
Модели экспертных оценок. К услугам экспертов прибегают в случае слабоформализуемых задач. В основе – методики организации экспертных оценок и их обработки (пример: балльная система). Количественная оценка мнений экспертов – методы ранга (эксперт присваивает произвольный ранг каждому фактору), шкальных оценок (факторы оцениваются по заранее выбранной шкале), парных сравнений (попарное сравнение альтернатив).
Класс задач принятия решения определяется тремя факторами - целью решения задачи выбора, типом "среды" задачи (всей совокупности неконтролируемых параметров), количеством критериев – и существенно зависит от видов имеющихся неопределенностей.
Неопределенность "среды" (неопределенность природы, формулировки целей и критериев) – имеется несколько возможностей, каждая из которых может реализоваться произвольным или случайным образом. Действий реального "противника" (конкурента) или партнера, преследующего свою цель и обладающего своими управляющими параметрами (активными средствами);
Природа неполноты информации может быть самой различной, обуславливаться разнообразными источниками. Виды неопределенностей: неизвестность, неполнота, случайность, нечеткость формулировок целей.
Множество неконтролируемых факторов может состоять из подмножеств: фиксированных случайных факторов (стохастические факторы) с известными законами распределения, факторов природной неопределенности с неопределенным законом распределения, неопределенных факторов, связанных со стратегиями поведения разумного противника, множество возможных проектных решений.
Для определения метода принятия решения необходимо определить структуру информационной ситуации: к какой информационной ситуации следует отнести неконтролируемый фактор (природа неопределенностей, известно или неизвестно распределение вероятностей, расплывчатость имеющейся информации).
Решение проблемы принятия проектных решений и их оптимизации в условиях многофакторной неопределенности требует формирования процедур принятия решений, позволяющих значительно снизить уровень неопределенности. Построение структуры системы неопределенностей и выбор методов принятия решений – субъективный фактор (также имеет неопределенность).
Возможные процедуры: формирование списка факторов природной неопределенности и системы (каталога) информационных ситуаций, присвоение каждому фактору свойственную ему конкретную информационную ситуацию.
Дальнейший путь уменьшения размерности неопределенности – операция "информационного сходства" - выделение близких информационных пар "фактор – информационная ситуация"
Нечеткость формулировки задачи приводит к необходимости пользоваться качественными критериями, характеризуемыми понятиями "предпочтение" "полезность". Термин "предпочтение" отображает качественную характеристику объекта, термин "полезность" – количественное представление предпочтений.
При различной конкретизации задачи снятия неопределенности она приобретает различный смысл и требует различных методов решения.
При выборе в условиях статистической неопределенности, особенно при задании условий внешней среды для системы (например, для проектирования системы необходимо знать, на какой глубине находится нефть, если в результате геофизической разведки получена некоторая совокупность чисел), или при разработке математической модели (как влияет солнечная активность на долговечность солнечных батарей). Основным предположением при формализации подобных задач является предположение о статистичности данных. Оно состоит в том, что связь между истинной, но неизвестной искомой закономерностью и наблюдаемыми данными адекватно описывается распределением вероятностей. Такую задачу можно решить методами теории игр – "игры против природы". Выбор закономерности на множестве возможных закономерностей (протоколы наблюдений) и действительное состояние природы (искомая закономерность) можно в совокупности охарактеризовать функцией потерь, которую и рассматривать как платежную функцию игры.
Применение статистических методов также вносят свою неопределенность. На качество решения влияют и заблуждения относительно статистичности наблюдений, и принятый протокол наблюдений, и применение процедуры, не соответствующей уровню и типу информации, и неверная содержательная информация статистического вывода.
Во всех случаях неполноты знаний, нечёткой или стохастической входной информации, будут носить нечёткий или вероятностный характер и результаты исследований, а принятые на основании этих исследований решения приведут к неоднозначным последствиям. В случае нечёткой (по своей природе) или неполной (при ограниченных возможностях проектанта) информации необходимо учитывать закономерности устойчивых состояниях и устойчивых траекторий системы. Должны быть выявлены и оценены, хотя бы на интуитивном уровне, все возможные, в том числе кажущиеся маловероятными последствия принимаемых решений, а также предусмотрены обратные связи, которые обеспечат своевременное вскрытие и локализацию нежелательного развития событий.
Моделирование принятия решения
Принятие решения может быть формализовано как выбор управления, переводящего систему из заданного состояния в желаемое. Такой выбор осуществляется с использованием математической модели принятия решения. При построении модели реальная операция неизбежно упрощается, схематизируется, с тем, чтобы ее можно было описать и затем исследовать с помощью того, или иного математического аппарата.
Общая модель операции выработки решения может состоять из совокупности тесно связанных моделей процесса операции (включая модель управляемой системы и модель обстановки проведения операции) и принятия решения.
Полной информации о внешних факторах до проведения операции чаще всего оперирующая сторона (проектант) не имеет. В такой ситуации наличие неопределенных факторов не позволяет однозначно определить фазовые переменные, следовательно, и течение операции оказывается непредсказуемым. Единственный выход – сформировать принципы принятия решений (правила, стратегии поведения), которые гарантируют определенный исход операции (либо действовать "на авось", что редко приводит к приемлемым результатам). Информация может поступить в ходе операции, что должно быть учтено при выработке возможных способов действий оперирующей стороны (правил принятия решений).
Правила поведения (стратегия принятия решений) должны исходить из достижения цели операции. Цель операции может быть достигнута не единственным способом действий, и для отбора наиболее экономного, эффективного из числа допустимых служит критерий эффективности. Всякий выбор зависящих от оперирующей стороны параметров называется решением.
При выборе оптимальной стратегии поведения задача выбора управления формулируется как задача отыскания векторной функции, доставляющей экстремальное значение целевому функционалу. На компоненты вектора управления (векторной функции) обычно накладываются ограничения.
Прогнозирование в принятии решений
Жизненный цикл многих сложных систем может составлять не один десяток лет. Поэтому при проектировании крайне трудно учесть все вопросы, связанные с прогнозированием развития системы и ее взаимодействием с внешней средой в будущем. Данная проблема должна рассматриваться уже на начальных стадиях проектирования, так как успешность ее решения во многом определяет эффективность системы в целом.
Прогноз – вероятностное суждение о состоянии объекта (процесса или явления) в определенный момент времени в будущем и (или) об альтернативных путях (сценариях) их достижения.
Сопутствующие понятия – предсказание (основано на логической последовательности – "достоверно будет"), предвидение (опережающее отражение действительности, основанное на познании законов развития - "должно быть"). Предвидение – более широкое понятие, включающее в себя прогноз и предвидение.
Прогнозирование (научно-техническое) - это специальное методическое исследование перспектив развития какой-либо системы, организации, отрасли. Прогнозирование имеет своей целью разработку прогноза - предсказания (обычно в форме вероятностного суждения) о состоянии этой системы в будущем. Объектами прогнозирования (в узком смысле) являются системы и процессы, развитие которых существенным образом определяется решениями людей (функциональные, эргативные, управляемые системы).
Сложность прогнозирования обусловлена не только сложностью проектируемой системы, но и необходимостью одновременного рассмотрения прогнозов развития науки и техники, производственных процессов, ограничений, определяемых социально-экономическими и экологическими причинами. Таким образом, понятие объекта прогноза значительно расширяется.
Одна из попыток дать универсальное определение понятия объекта прогноза – в виде собирательного понятия технологии, включающего широкую область целенаправленного применения физических наук, наук о жизни, наук о поведении. Чтобы получить достоверную информацию о будущем необходимо знание законов развития общества, хозяйства, науки и техники, знать причины и движущие силы этого развития. В этой терминологии технологическое прогнозирование – получение вероятностной оценки будущего изменения (перемещения) технологии, определяемого прежде всего техническим прогрессом.
Процесс изменения характеристик системы, являясь частью общего процесса развития, характеризуется чередованием участков постепенного (эволюционного) и резкого (скачкообразного) развития. Примеры скачкообразного развития: использование новых физических принципов, идей, решений в вычислительной технике.
В нынешнем процессе научно-технического прогресса наблюдается тенденция учащения скачков и рост величины самих скачков. Различаются скачки разных категорий (по мере убывания влияния на развитие): использование новых принципов, реализация новых решений в рамках одного принципа, совершенствование технологий изготовления.
Для управляемых систем различают два основных вида прогнозирования: поисковое и нормативное. Поисковое (генетическое) прогнозирование - это предсказание состояния в будущем при наблюдаемых тенденциях в предположении, что последние не будут изменены посредством планов, проектов, решений и т.п. Результатом поискового прогнозирования является так называемый эталонный или опорный прогноз. Нормативное (проектное) прогнозирование - это предсказание путей достижения желательного состояния объекта исследования на основе заданных целей и критериев с оценкой возможностей и ограничений. Нормативное прогнозирование часто служит основой стратегического планирования.
Таким образом, прогнозирование тенденций и направлений развития систем направлено не на категоричное предсказание, а на изучение вероятного и желательного состояния объекта исследования, что достигается сопоставлением данных поискового и нормативных прогнозов. Конечный практический результат - повышение обоснованности решений (планов, проектов, программ).
По сроку прогноза (времени упреждения) прогнозирование разделяется на текущее, краткосрочное, среднесрочное, долгосрочное, сверхдолгосрочное. Обычно эшелоны прогнозирования приравниваются к эшелонам планирования: краткосрочные - от 1 года до 2 лет, среднесрочные - от 5 до 10 лет, долгосрочные - от 15 до 20 лет, сверхдолгосрочные - от 50 до 100 лет. Наиболее широко здесь применяются среднесрочные прогнозы на срок от 5 до 10 лет. Глубина прогнозирования тесно связана с временными скачками технологии.
Организация прогнозирования.
В основе организации прогнозирования лежат общие принципы исследования сложных систем, предлагаемые исследованием операций и системным анализом.
Основные этапы прогнозирования:
- постановка задачи, отбор необходимой информации;
- выбор критерия или системы критериев;
- формирование прогнозирующей модели;
- осуществление прогноза;
- анализ результатов;
- выработка практических рекомендаций по реализации прогноза.
Прогнозирующая система включает собственно исследователей, комплекс технических, программных и математических средств.
На этапе постановки задачи четко определяется объект прогноза и цель прогнозирования. Тип и объем информации определяется объектом прогноза и поставленными целями, включает в себя прошлые и настоящие данные об объекте и его аналогах.
Методы прогнозирования.
По степени формализации все методы делятся на интуитивные и формализованные.
Интуитивные методы применяются тогда, когда объект либо слишком прост, либо настолько сложен, что аналитически учесть влияние многих факторов практически невозможно. В этом случае применяют эвристические методы, в частности методы экспертных оценок.
Группы формализованных методов: статистико-математические, ассоциативные, информационные, системно-структурные.
Статистико-математические методы – фактическая обработка статистического материала и получение на его основе математических зависимостей для последующих экстраполяций. Эти методы включают в себя методы экстраполяции, огибающих кривых, статистическое моделирование, корреляционное и регрессионное моделирование, числовая аналогия, математическое программирование. Наибольшее распространение получили методы экстраполяции тенденций. Эти методы основаны на предположении об определенном постоянстве закономерностей развития объекта в течение заданного времени (для периода времени без скачков).
Ассоциативные методы – имитационное моделирование, историко-логический анализ.
Информационные методы – анализ потоков публикаций, значимости изобретений, патентной информации.
Системно-структурные методы – функционально-иерархическое моделирование сценариев, структурная аналогия.
На основе общей методологии прогнозирования разрабатываются частные методики прогнозирования развития конкретных систем.
Конкретные методики прогнозирования, как правило, образуются путем сочетания нескольких методов в соответствии с предметом, целью и задачами проектирования.
Неотъемлемой частью процесса прогнозирования является накопление и оперативное использование больших объемов информации в формализованном виде (базы данных, информационно-поисковая система), а также знаний экспертов.
10 Особенности синтеза модели (проекта) технической системы
10.1 Особенности синтеза модели технической системы
Этапы проектирования
Принято пять этапов проектирования: техническое задание, техническое предложение, эскизный проект, технический проект, рабочая документация.
Укрупненная логическая схема проектирования представлена на рисунке.
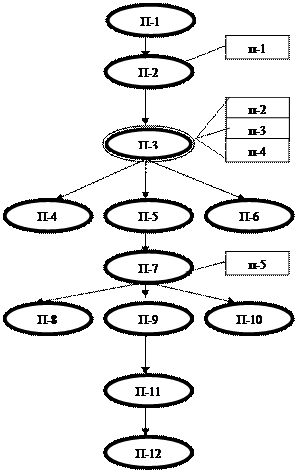
| 1. Определение потребности в системе, прогнозирование условий функционирования 2. Формулировка технического задания на разработку системы 3. Анализ альтернативных вариантов, разработка технического предложения 4. Эскизное проектирование 5. Экспериментальная отработка основных решений 6. Отработка конструкторских и технологических решений 7. Техническое проектирование 8. Создание опытного образца 9. Разработка программы испытаний 10. Проведение испытаний 11. Корректировка рабочей документации по результатам испытаний 12. Выпуск технической документации Дополнительные процедуры: п1 – формулировка концепции системы п2 – сравнение вариантов концепции п3 – структурная оптимизация п4 – параметрическая оптимизация п5 – детальное проектирование |
Логическая схема проектирования
Техническое задание на разработку системы содержит цели и задачи системы, концепцию создания системы. Выполнение поставленной цели в концепции рассматривается с помощью различных видов систем, различных классов одного вида системы, различных типов систем внутри одного класса и вида.
Техническое предложение содержит техническое и экономическое обоснование разработки системы, облик системы – укрупненная структура и основные характеристики системы, которые позволят начать разработку эскизного проекта системы. При этом анализируется политическая и экономическая обстановка, исследуются целесообразные сферы и способы применения системы, возможности научно-технической и технологической реализации проекта. На этом этапе рассматривается множество возможных вариантов системы, оценивается эффективность каждого, выбирается вариант для дальнейшей разработки.
Эскизный проект содержит принципиальные решения, дающие представления об устройстве и принципе работы системы, ее основные проектные параметры.
Технический проект содержит окончательные детальные технические решения, дающие возможность подготовить рабочую документацию.
Рабочая документация содержит описание системы, дающее возможность ее изготовить.
Первые три этапа - техническое задание, техническое предложение, эскизный проект – обычно называются внешним проектированием, другие два - технический проект и разработка рабочей документации – внутренним проектированием.
Проектируемая система выступает, с одной стороны, как часть системы более высокого уровня, с другой – как система для объектов более низкого уровня (подсистем). В соответствии с этим процесс проектирования состоит из двух основных этапов: внешнего проектирования и внутреннего проектирования.
В соответствии с двумя основными классами задач – системное и детальное проектирование - различают два основных класса моделей – быстрые и поверочные модели (в каждой из них может быть несколько уровней точности).
На системном уровне модели обычно строятся по принципу «от простого к сложному» – модели уточняются в процессе проектирования по мере расширения наших знаний о системе.
На более поздних стадиях системных исследований иерархия математических моделей может строиться и по противоположному принципу: «от сложного к простому».
При построении моделей по принципу «от простого к сложному» каждый следующий шаг уточняет более простую модель после ее подробного изучения. Возникает цепочка (иерархия) все более полных моделей, каждая из которых обобщает предыдущие, включая их в качестве частного случая. Путь «от простого к сложному» дает возможность изучать все более реалистичные модели и сравнивать их свойства.
При построении моделей по принципу «от сложного к простому» из достаточно общей и сложной модели при упрощающих предположениях получается последовательность все более простых (но имеющих уменьшающуюся область применимости) моделей. Путь от общего к частному позволяет сразу установить некоторые общие свойства системы, конкретизируя и дополняя их в частных ситуациях, дает возможность проводить многочисленные оптимизационные расчеты.
На базе детализированной хорошо обоснованной модели, полученной на основании детально проработанного опорного варианта, создается ее упрощенный аналог, отражающий все основные связи и ограничения, необходимые для решения конкретной задачи. При необходимости для ограниченного количества опорных вариантов корректируются принятые проектные решения.
Особенности проектирования адаптивных систем
Условия применения систем и требования к ним непрерывно изменяются, и, несмотря на прогнозы и сценарии, любая ранее созданная система станет перед необходимостью приспособления к новым условиям. Неучет этого фактора при проектировании приведет в будущем к быстрому моральному старению системы, потере конкурентоспособности, сокращению жизненного цикла.
Возможность адаптируемости (приспособления) системы к будущим условиям применения – один из критериев оценки качества системы.
Для конкретных условий применения системы ее основные проектные параметры могут быть с достаточной степенью оптимальности определены на основе проектных проработок, моделирования, экспериментальной отработки. Для адаптации системы к будущим условиям применения необходимы такие проектные решения, которые позволят обеспечить максимальную эффективность системы в изменившихся условиях.
Этап формирования облика характеризуется множеством неопределенных факторов. Идеальное планирование работ и принятие решений состоят не в том, чтобы предусмотреть все возможные ситуации и рекомендовать соответствующие решения по применению системы, а в том, чтобы спланировать возможность маневрирования ресурсами при изменении ситуации.
Принятые на этапе проектирования решения определяют эффективность системы на весь период ее жизненного цикла и являются необратимыми. Выбор адаптивных систем предусматривает анализ информации о неопределенных факторах.
При выборе адаптивных технических решений возникает противоречивая ситуация, требующая неформальной оптимизации. С одной стороны, отсутствие адаптивных решений не может обеспечить высокую эффективность системы для достаточно широкого диапазона условий применения. С другой, - предельная степень адаптации к неопределенным условиям связана со значительными затратами, сложностью реализации, возможностью принятия рискованных (невостребуемых впоследствии) проектных решений. Поэтому необходимо обоснование степени адаптации на основе оценки эффективности системы в широких условиях применения с учетом затрат и сроков создания.
Неопределенные факторы обусловлены не только отсутствием сведений о характеристиках системы и условий применения, но и – в наиболее общем случае, характерном для конкурирующих систем, - факторами, направленными на уменьшение эффективности системы.
Наивысшая степень адаптации всех компонентов системы на всех этапах жизненного цикла – разработка алгоритма применения, позволяющего изменять параметры и варианты действий системы по мере получения информации в процессе операции (например, на борту ЛА, танка). Выбранные технические решения должны позволять это делать.
Системы, гибко реагирующие на условия операции, называют адаптивными или системами параметрической компенсации.
Возможны две предельные схемы параметрической компенсации: компенсация неопределенности до непосредственного применения (до операции) и в процессе применения (в ходе операции).
Компенсация до операции предусматривает изменение проектных параметров в процессе эксплуатации при уточнении условий применения: может быть реализована созданием адаптивно-модульных конструктивных схем элементов на основе разработки унифицированных элементов конструкций (модулей) с последующим их комплектованием в различных вариантах в зависимости от условий эксплуатации.
Компенсация в ходе операции связана с изменением параметров на основе перераспределения располагаемых ресурсов или за счет других, предусмотренных в конструкции возможностей. Обеспечивается системой управления.
Возможные пути компенсации неопределенности:
- применение набора вариантов систем различной степени специализации, каждый из которых является оптимальным в определенных условиях (в том числе, набор вариантов комплектования одной системы разнотипными компонентами – например, кухонный комбайн, различные боекомплекты на самолете, танке),
- реализацию «гибких» технических решений (многофункциональные системы, многорежимные агрегаты),
- оптимальные стратегии использования систем (перераспределение ресурсов и функций компонентов системы).
Исследование эффективности адаптивных систем связано с использованием методов прогнозирования, имитационного моделирования, игровых подходов для анализа конфликтных ситуаций.
Если для монопараметрической (без адаптации) системы задача оценки эффективности решается для каждого из вариантов системы, то для адаптивных систем оценка эффективности осуществляется с учетом анализа технических гибких решений, синтеза алгоритмов применения.
Основные особенности исследования эффективности систем с адаптивными компонентами:
- математическая модель операции должна отражать возможность изменения параметров каждого из рассматриваемых вариантов проектируемого компонента в зависимости от информации об условиях применения, изменяющихся как до, так и в ходе операции
- выбор вариантов проектируемых адаптивных компонентов может основываться на их сопоставлении с аналогичными вариантами, не реализующими адаптивные возможности.
- к числу варьируемых относится только часть параметров, обеспечивающих адаптивные возможности системы, для каждого из компонентов адаптивной системы рассматриваются возможные пути адаптации (модульность, изменение конструкции).
Моделирование функционирования технической системы
Особенности построения моделей при проектировании
В процессе проектирования с использованием математических моделей решаются следующие задачи:
- формирование структуры и выбор основных проектных параметров;
- определение оптимальных режимов функционирования системы и ее элементов в различных условиях внешней среды и оптимальная организация взаимодействия элементов;
- учет неопределенностей функционирования системы при оценке ее эффективности.
Построение моделей – процедура неформальная. Модель не только должна правильно отражать явления, но и быть удобной для пользователя – степень детализации и способы представления модели для каждой решаемой задачи зависят от пользователя.
Для каждого этапа проектирования вырабатываются стандартные приемы моделирования и общие способы работы с этими моделями.
Модель на системном уровне обеспечивает взаимосвязь критериев эффективности и основных параметров системы с учетом внешней среды. В состав модели системы в целом входят те структурные компоненты, параметры которых признаны определяющими для эффективности системы. Устанавливается физическая и функциональная зависимости (структура и поведение системы), определяются соотношения между параметрами системы, внешней среды и параметрами каждого компонента системы, которые влияют на критерии эффективности системы, составляется иерархия моделей. Модель должна позволять исследовать влияние параметров системы и среды на эффективность (анализ чувствительности).
Исходя из основных принципов системного подхода - модель строится как единое целое, все элементы, связи, действия системы подчинены достижению конечной цели (каждый компонент системы разрабатывается так, чтобы обеспечить системе достижение цели с максимальной эффективностью), строится иерархия моделей исходя из иерархического характера системы, обеспечивается совместное рассмотрение структуры системы и ее функций;
Многоуровневость технической системы и моделей определяется большой размерностью задачи и связанной с этим необходимостью ее декомпозиции на частные подзадачи с передачей информации от одной к другой. Каждая из подзадач имеет свои критерии, связи и ограничения, но в совокупности они должны давать возможность решать общую задачу. Образование иерархии самостоятельных подзадач ведет к уменьшению размерности, но является источником неопределенностей в связи с несовпадением их целей.
Возникает неформализуемая проблема не только выделения подзадач, но и определения их состава и глубины исследований.
Схема многоуровневого представления сложной технической системы
 |
Уровень I представлен самой системой, уровень II – ее агрегатами и подсистемами, уровень III – узлы агрегатов и подсистем, уровень IV – детали узлов.
Система может быть представлена множеством моделей, каждая из которых отражает определенную грань условий ее физического и функционального существования. Это дает возможность исследовать и выявить свойства системы, используя ряд узкоориентированных моделей. Основная специфика построения таких моделей – их согласование, обеспечивающее координацию принимаемых проектных решений.
Укрупненное исследование системы заключается в игнорировании детальной структуры системы и анализе только общего поведения системы как целого, в оценке ее интегративных характеристик. Цель состоит в создании модели системы в ее взаимодействии с окружением (модель "вход – выход"). На этом уровне формируются общие представления о системе. Единая модель всей сложной системы – укрупненная модель – создается для формирования концепции системы – для приблизительных оценок качества системы.
На начальном этапе проектирования строится опорный вариант модели, укрупненные блоки которой используются для построения моделей альтернативных систем. Степень детализации модели, форма представления определяются задачами каждой проектной процедуры.
В соответствии с двумя основными классами задач – системное и детальное проектирование - различают два основных класса моделей – быстрые и поверочные модели (в каждой из них может быть несколько уровней точности).
На системном уровне модели обычно строятся по принципу "от простого к сложному" – модели уточняются в процессе цикличного проектирования по мере расширения наших знаний о системе.
На более поздних стадиях системных исследований иерархия математических моделей может строиться и по противоположному принципу: «от сложного к простому».
На основе детализированной хорошо обоснованной модели (например, опорного варианта системы) создается ее упрощенный аналог, отражающий все основные связи и ограничения, необходимые для решения системной задачи - выбора концепции, структуры и основных проектных параметров. При необходимости создаются модели на основании ограниченного количества опорных вариантов и корректируются принятые решения.
На любой стадии проектирования, при любой степени детализации модели типичная последовательность работ при построении моделей:
1. Выявление главных функций системы (цели, назначение, свойства), формирование и определение основных понятий, используемых в системе.
2. Выявление основных компонентов системы и их функций, их единства в рамках системы, выявляются укрупненная структура системы и характеристики основных связей, выявляются системообразующие факторы – те связи и взаимообусловленности, которые и делают систему системой.
3. Выявление основных процессов в системе, их роли и условий осуществления, выявление смены состояний в функционировании системы. В системе с управлением выявляются основные управляющие факторы.
4. Выделение системы из внешней среды, определение границ системы, выявление характера связей с внешней средой. Исследуются внешние воздействия на систему (входы), определяется их тип (вещественные, энергетические, информационные), степень влияния на систему, основные характеристики.
5. Выявление неопределенностей и случайностей в системе, степени их влияния на систему.
Структура системы, связи, значимость каждого элемента выявляются в результате спирального (все более углубляющегося на каждом витке) повторения исследований на основе этих моделей.
Аналитические модели дают возможность получения приближенного, но отражающего основные закономерности решения задачи, выявить основные зависимости и определить направления дальнейших исследований.
Модели с использованием численных методов могут быть более точными, но менее полными, что ограничивает исследования небольшим числом вариантов или частных реализаций процесса.
Приближенное решение точно сформулированной задачи предпочтительнее решения упрощенной задачи точными методами оптимизации: точная формулировка задачи дает возможность осуществить оценку сложных взаимосвязей между многими элементами. Даже если модель и не обеспечит получения строго оптимального решения задачи (чего практически никогда невозможно достичь), но в ней будут учтены все важные факторы, что окажется более полезным, чем оптимальное решение нечетко сформулированной задачи.
При моделировании сложных процессов далеко не всегда можно модель преобразовать в систему уравнений, пригодную для применения численных методов.
Имитационное моделирование – исследование свойств системы путем воспроизведения процесса ее функционирования. Это одна из разновидностей эксперимента с математической моделью системы.
Имитационное моделирование при синтезе системы позволяет решать следующие задачи:
- обоснование и проверка принятых технических решений, поиск новых;
- получение данных для более простых моделей системы;
- проверка результатов, полученных на более простых моделях, для обоснования принятых на этих моделях допущений.
Модель функционирования системы определяет поведение системы в пространстве и во времени под влиянием тех или иных воздействий, в том числе неопределенных. Для описания множества входных воздействий требуется моделирование внешней среды (моделирование обстановки проведения операции).
Пример космического корабля для исследования планеты. Здесь отыскания такого управления кораблем, которое обеспечит попадание его в заданную точку пространства (на планету) недостаточно. Необходимо посадить аппарат на поверхность планеты – здесь уже задача решается в условиях неопределенности: неизвестны условия внешней среды – условия функционирования аппарата, что значительно влияет на конструкцию и выбор оптимальных ее параметров. Это неопределенности природного характера.
Главным является моделирование функционирования каждого компонента системы с учетом его связей с другими компонентами и влияния на эффективность системы в целом.
Также как и весь процесс проектирования, построение моделей имеет циклический итеративный, спиралевидный характер с последовательным расширением понимания системы на каждом шаге с постепенным углублением исследований и пониманием системы, ее сущности, условий функционирования и эффективности.
Система представляется множеством узкоориентированных моделей, каждая из которых отражает определенную грань условий ее физического и функционального существования, что дает возможность исследовать и выявить различные свойства системы. Основная трудность при этом – учет связей между отдельными моделями (согласование моделей).
Для обоснования принятия решения о наилучшем способе достижения системой заданной цели функционирования необходимо на моделях исследовать различные ситуации, которые могут возникнуть при функционировании системы.
Модель функционирования (функциональная модель) должна обеспечивать прогнозирование процесса функционирования по заданным начальному состоянию системы и параметрам процесса.
В модели устанавливаются функциональные зависимости, определяющие поведение системы - соотношения между параметрами системы, внешней среды и критериями эффективности для системы в целом и каждого из ее основных компонентов. В состав системы входят только те компоненты, параметры которых признаны определяющими. Исследуется влияние изменения параметров системы и среды на эффективность (анализ чувствительности).
Традиционное требование при построении моделей – замкнутость. Замкнутость модели процесса функционирования (протекания операции) означает следующее.
При известной информации о внешних по отношению к модели факторах операции можно восстановить (в силу объективных законов, формальным выражением которых является модель операции) состояние операции на любой заданный момент времени.
При известном начальном состоянии операции, известных на некотором интервале времени параметрах модели и управления, совокупность связей между ними (т.е. модель процесса) позволит определить на данном интервале времени все фазовые переменные и тем самым иметь полное представление о состоянии операции на этом интервале времени.
Величины, входящие в модель подразделяются на три основные группы.
Фазовые переменные (внутренние – эндогенные) – определяют состояние операции на данный момент времени. Если эти переменные известны на некотором интервале времени, то считается, что состояние операции на этом интервале полностью определено. Чаще всего фазовые переменные являются искомыми функциями и должны определяться из самой модели операции.
Внешние переменные (экзогенные) – параметры, которые не определяются в модели, а должны быть тем или иным способом заданы извне. Эти переменные не зависят от воли оперирующей стороны.
Управления – переменные, которые может формировать оперирующая сторона.
Формирование технического облика системы
Технический облик системы – модель системы (вербальная), в которой представлены перечень задач системы, ее структура и основные проектные параметры, основные характеристики функциональных подсистем.
В структуре системы учитываются только основные элементы, критичные при определении соответствия системы поставленным целям и при оценке эффективности системы.
Задача выбора оптимального облика системы решается при декомпозиции ее на две задачи: структурную и параметрическую оптимизации (синтез и анализ системы).
При создании моделей сложных систем строятся две взаимосвязанные модели: структурно-параметрическую модель системы и модель функционирования системы.
Структурно-параметрическая модель системы должна выявить разбиение системы на подсистемы, расположение подсистем, их параметры и связь между ними. Такая модель необходима для выбора структуры системы. Структурно параметрическое описание системы может помочь созданию модели функционирования системы - создаются модели функционирования подсистем, которые затем объединяются в общую систему.
В процессе структурного проектирования (при формировании концепции) создается единая укрупненная модель всей системы, целью которой является приближенная сравнительная оценка эффективности альтернативных вариантов концепций (структуры и состава основных компонентов) для выбора наилучшей (нескольких). При этом игнорируется детальная структура системы и анализируется только общее поведение системы как единого целого, оцениваются ее интегративные характеристики и взаимодействие ее с внешней средой.
Формирование структуры системы
При анализе эффективности системы решаются прямая и обратная задачи. Прямая задача - эффективность системы оценивается для выбранных ее концепции и… Процесс постановки задачи синтеза является сложным и не поддается… Процесс начинается с изучения задачи в содержательном и организационном аспектах.Выбор основных проектных параметров системы
Из основных проектных параметров системы {P} выделяются структурные параметры {S} (определяют структурную схему системы) и проектные параметры {p}… Неопределенность условий применения не позволяет однозначно выбрать… Для заданных условий функционирования системы определяются ее основные проектные параметры, обеспечивающие выполнение…Формирование множества вариантов системы
Генерирование множества вариантов (альтернатив) – идей о возможных способах достижения цели является творческим процессом. Здесь методология одна – выявляют и формируют эвристические, неформальные правила, которые во многих случаях приводят к успеху: прогнозные оценки развития общества и техники, анализ специальной литературы, привлечение экспертов.
Методы: мозговой штурм, деловые игры, имитационное моделирование, комбинирование имеющихся альтернатив, вплоть до полного перебора.
При проведении структурного и параметрического анализа варианты системы формируются на основе детально проработанных опорных вариантов для различных структур и условий применения системы.
Для формирования исходного множества вариантов необходимо:
- установить границы областей допустимых решений;
- на основе параметрического анализа сформировать варианты в области допустимых решений;
- детально разработать необходимое число математических моделей опорных вариантов.
Основой построения исходного множества вариантов заданной структуры является параметрический анализ опорного варианта: задание множества вариантов изменения проектных параметров с последующим сопоставлением каждому вектору параметров {р} системы соответствующих векторов параметров подсистем {p} и, наоборот.
Для построения вариантов на базе опорного требуются параметрически трансформируемые блочные математические модели подсистем и элементов. Такие модели позволяют генерировать дополнительное множество вариантов в окрестностях опорного для выбора из них рационального варианта.
Из множества допустимых вариантов системы, удовлетворяющих связям математической модели, вытекает основная задача формирования облика системы – определить те параметры, которые обеспечивают максимальную эффективность системы.
Особенности методологии выбора рациональных параметров системы обусловлены большим количеством оптимизируемых параметров, сочетанием дискретной и непрерывной природы их изменения, неопределенностью условий применения системы. Это делает необходимым проведение раздельной оптимизации параметров дискретной и непрерывной природы, что предъявляет свои требования к декомпозиции общей задачи и проведения параметрических исследований.
Выбор рационального варианта предусматривает определение такого из исследуемых вариантов, который обеспечивает максимальную эффективность системы с учетом диапазона неопределенностей внешней среды.
Обобщенная схема выбора рационального варианта системы
1. Формирование множества вариантов структур системы и оптимизация проектных параметров для каждого варианта структуры.
Для каждого варианта структурных (дискретных) параметров {S} анализируются параметры непрерывного изменения - проектные параметры {р}, выделяются параметры, оказывающие влияние на выбор структуры системы (проводятся параметрические исследования и анализ влияния проектных параметров {р} на различные варианты структуры), определяются оптимальные значения проектных параметров {р }* для заданной структуры.
2. Сравнительная оценка эффективности вариантов структур и выбор рациональных значений структурных и основных проектных параметров системы.
Проводятся параметрические исследования в области оптимальной точки с целью определения тенденций изменения параметров при отклонении исходных данных и условий применения от заданных, чувствительности критерия эффективности к изменению параметров.
Различают локальный и глобальный уровни исследований.
Локальный уровень – исследования параметров подсистемы проводится независимо от системы более высокого уровня.
Глобальный уровень – исследования параметров подсистемы проводятся в широкой области изменения параметров и условий применения системы в целом с корректировкой задач, критериев, ограничений. При этом устанавливается взаимосвязь основных проектных параметров системы и параметров подсистем, функционирующих в составе системы в различных условиях применения.
Методы сравнения вариантов
Метод косвенного сравнения вариантов: по параметрам сравниваемых вариантов, по обобщенным показателям, по потенциальным возможностям – без вычислений абсолютных значений показателя эффективности – используются для предварительного отбора вариантов для оценки непосредственными методами.
Методы непосредственного сравнения вариантов базируются на оценке эффективности каждого варианта для различных структур и условий применения.
Результирующая матрица может быть получена в виде:
| U1 | U2 | … | Uj | … | Un | |
| {a}1 | W11 | W12 | W1j | W1n | ||
| {a}2 | W21 | W22 | W2j | W2n | ||
| … | … | … | … | … | … | … |
| {a}i | Wi1 | Wi2 | Wij | Win | ||
| … | … | … | … | … | … | … |
| {a}m | Wm1 | Wm2 | Wmj | Wmn |
где {a}i , i = 1,m – сравниваемые варианты проектируемого элемента
Uj , j = 1,n – варианты условий применения.
Использование полученной матрицы для выбора рационального варианта встречает затруднения: сравнение вариантов возможно только для одного варианта условий применения исходя из max Wij, для диапазона условий применения { U1 , U2 , …, Un } однозначного преимущества какого либо варианта, как правило, не бывает.
Задача сравнения вариантов в этом случае может рассматриваться как задача принятия решений в условиях неопределенности. Недостатки метода – большой объем расчетов и сложность учета широкого диапазона условий применения.
10.2 Концепции автоматизации проектирования
Термин «автоматизация проектирования» предполагает не автоматическое проектирование вплоть до получения готового результата, а средства, предоставляемые проектанту для проектирования.
Эти средства охватывают очень много различных по своему содержанию понятий. Например:
- чисто технологические средства для решения рутинных и шаблонных задач автоматизации графических работ, обработки данных, СУБД;
- создание «виртуальных макетов» проектируемых объектов;
- технико-экономическое обоснование проектных решений, прогноз и контроль процессов производства.
Концепции САПР рассматривается на основании системного подхода с учетом истории ее развития.
История развития САПР
Историю развития САПР можно достаточно условно разбить на три основных этапа, каждый из которых длился, примерно, по 10 лет, начиная с 70-х годов.
На начальном этапе, в 70-е годы показана принципиальная возможность автоматизации проектирования. Наиболее простой, соответствующей тогдашнему уровню техники, стала задача автоматизации графических работ. Появились графические системы для вычерчивания на экране узлов и деталей конструкций, позволяющие ускорить разработку и доработку конструкций, уменьшить вероятность появления технических ошибок, интерактивные графические системы подготовки производства. Появились первые системы подготовки технической документации, обеспечивающие автоматизированный выпуск рабочих чертежей. В это время и появился впервые термин САПР. На этом этапе проектанты работали на громоздких компьютерных системах с разделением ресурсов (по устанавливаемым приоритетам).
В 1971-м появилась компания Manufacturing and Consulting Services (MCS), оказавшая огромное влияние на развитие САПР - идеи MCS составили основу почти 70% современных САПР. Большинство таких систем предлагали фирмы, продававшие одновременно аппаратные и программные средства.
На втором этапе, в 80-е годы графические системы стали превращаться в графоаналитические САПР: на экране формируется изображение или расчетная схема проектируемого объекта, что эквивалентно введению информации в память ЭВМ, затем с помощью расчетных модулей решаются задачи анализа конструкции. Полученные результаты обрабатываются и выдаются на экране графического дисплея в виде эпюр, гистограмм, графиков и т. д. – появились пакета анализа сложных конструкций. В первоначальный проект могут быть внесены изменения - за определенное число итераций может быть получено оптимальное проектное решение. Подобные графоаналитические САПР в основном ориентированы на проектирование небольших узлов и деталей.
В этот период появились первые пакеты, позволяющие частично автоматизировать процесс подготовки производства с помощью программ для станков с ЧПУ. К концу 80-х годов начали появляться специализированные САПР (электрические, механические, САПР летательных аппаратов, судов, автомобилей, электрических машин), стоимость графоаналитических систем снизилась, примерно, с 90 тыс.дол. до 20 тыс. дол. Системы постепенно стали переводиться на персональные компьютеры, появилась возможность работать в интерактивном режиме. Вычислительная мощность компьютеров значительно выросла.
Третий этап (90-е годы) характеризуется совершенствованием функциональности систем - появились расчетно-оптимизационные САПР, позволяющие осуществлять поиск оптимальных конструкций.
Одно из новых направлений - программно-экспериментальные комплексы, позволяющие осуществлять автоматизацию экспериментальных исследований. На крупных предприятиях организовываются замкнутые системы получения, обработки и передачи экспериментальной информации на вход других подсистем САПР, что позволяет осуществлять экспериментальную оценку полученных аналитических результатов.
Удешевилось производство технического обеспечения, повысилась его производительность, началось массовое распространение САПР.
Классификация САПР
Современные САПР можно классифицировать по ряду признаков – по целевому назначению, приложению, масштабам (комплексности решаемых задач), характеру базовой подсистемы – ядра САПР.
По целевому назначению различают САПР, обеспечивающие различные аспекты проектирования (системы функционального проектирования):
- системы конструкторского проектирования (черчение) - CAD (Computer Aided Design);
- системы проектирования технологических процессов (организация производства) - CAМ (Computer Aided Manufacturing);
‑ системы инженерных расчетов и анализа – системы CAE (Computer Aided Engineering).
По приложениям широко используются группы САПР для применения в различных отраслях: САПР машиностроительных отраслей – системы MCAD (Mechanical Computer Aided Design), САПР для радиоэлектроники - системы ECAD (Electronic Computer Aided Design). Среди них могут быть выделены специализированные САПР (летательных аппаратов, электрических машин).
По характеру базовой подсистемы различают:
САПР на базе машинной графики и геометрического моделирования – определение пространственных форм и взаимного расположения объектов – для автоматизации процесса конструирования.
САПР на базе СУБД – переработка большого объема данных при сравнительно несложных расчетах.
САПР на базе конкретного прикладного пакета – автономно используемые пакеты - системы расчетов и инженерного анализа – системы CAE.
Обслуживающие подсистемы – разработки и сопровождения программного обеспечения CASE (Computer Aided Software Engeneering).
По уровням решаемых задач может быть и такая классификация САПР:
- по уровню формализации решаемых задач - системы, построенные на полностью формализуемых методах решения проектных задач; ведущие проектные работы, не поддающиеся полной формализации; организующие поиск решения неформализуемых задач;
- по функциональному назначению - системы расчетно-оптимизационные; графические; автоматизированного проектирования конструкций; графоаналитические; подготовки технической документации; обработки результатов экспериментальных исследований; информационные; технологической подготовки производства (программ для станков с ЧПУ);
- по специализации - системы специализированные и инвариантные;
- по технической организации - системы с центральным процессорным управлением; комплектуемые автоматизированными рабочими местами конструктора (АРМ) с собственными вычислительными ресурсами.
Стратегическое развитие САПР
Современное состояние САПР
Процесс автоматизации проектирования идет от полностью автоматически выполняемых проектных операций и процедур до систем, обеспечивающих… Такие сквозные САПР создаются обычно только в крупных фирмах и предназначаются… Укрупненно структуру САПР можно представить в виде подсистем:Направления разработки проектной составляющей САПР
Очевидно, что в наибольшей степени влияет на эффективность создаваемой системы начальный этап проектирования – этап формирования концепции системы:… Автоматизация начального этапа проектирования (внешнего проектирования) –… Важность автоматизации работ начального, концептуалльного этапа проектирования демонстрирует статистика оценки цены…Файл-серверные информационные системы
Используется общее хранилище файлов на файл-сервере, каждый файл хранит данные с фиксированной структурой (различной для разных файлов). Компоненты информационной системы, выполняемые на разных ПК, взаимодействуют только за счет наличия общего хранилища файлов на файл-сервере. В классическом случае в каждом ПК дублируются не только прикладные программы, но и средства управления базами данных. Файл-сервер представляет собой разделяемое всеми ПК расширение дисковой памяти. Возможность выборки согласованной (по заданному критерию) информации из нескольких файлов не поддерживается.
Клиент-серверные информационные системы
Информационная система основана на использовании серверов баз данных.
Сервер баз данных - программный комплекс, привязанный к соответствующей базе (базам) данных, существующий независимо от пользовательских (клиентских) процессов.
Такое программное обеспечение выполняется (хотя и не обязательно) на выделенной аппаратуре. Конкретное воплощение программного комплекса и выделенной аппаратуры различается в разных серверах баз данных.
Серверы баз данных существенно сложнее по организации, чем СУБД-ФС, но обеспечивают более тонкое и эффективное управление базами данных.
Клиентская часть приложения взаимодействует с клиентской частью программного обеспечения управления базами данных, которая, фактически, является индивидуальным представителем СУБД для приложения.
Архитектура Интернет/Интранет
Информационная Intranet-система - это корпоративная система, в которой используются методы и средства Internet. Интранет — это «частный» Интернет, ограниченный виртуальным пространством отдельно взятой организации.
В основе реализации корпоративных информационных систем на базе данной архитектуры лежит принцип "открытой архитектуры" что во многом определяет независимость реализации корпоративной системы от конкретного производителя.
Такая система может быть локальной, изолированной от Internet, или опираться на виртуальную корпоративную подсеть Internet (в этом случае особенно важны средства защиты информации от несанкционированного доступа).
Хранилища данных и системы оперативной аналитической обработки данных
Следствием этого на сегодняшний день в большинстве организаций функционируют разнородные и слабо связанные между собой информационные системы,… Существующее состояние корпоративных информационных систем характеризуется… Информационные системы, ориентированные на решение подобного класса задач, получили название систем поддержки принятия…Предпроектные исследования
Рамки проекта включает определение объема работ, формирование организационной структуры проекта и формирование управления ним. Объем работ определяется исходя из главных целей создания информационной… Объем работ определяют следующие факторы:Постановка задачи
Системно-аналитическое обследование Цель обследования – получение моделей данных и описание процедур принятия… Основные задачи предпроектного обследования информатизируемых процессов:Проектирование системы
Архитектура процессов – определяется состав и содержание процессов преобразования и передачи данных. Архитектура программного обеспечения (компонентная архитектура) – определяется… Техническая архитектура – определяются физические узлы системы и связи между ними.Архитектура программного обеспечения
Общее программное обеспечение: - программное обеспечение сетевого доступа к приложениям и БД – сетевые и… - программное обеспечение загрузки и предварительной обработки данных, набор средств для загрузки данных из БД и…Подсистема администрирования.
Основные задачи подсистемы: администрирование доступа к данным, сопровождение профилей пользователей, разграничение доступа к конфиденциальным данным и защита информации от несанкционированного доступа.
В соответствии с системой управления проектом реализуются алгоритмы разграничения доступа различных категорий пользователей: к аналитическим приложениям, к номенклатуре доступных для анализа показателей (в соответствии с заданной тематикой пользователя), к данным по уровню детализации и полноте представления (в соответствии с рангом пользователя).
Инструментальные средства подсистемы должны позволять:
- определять объекты хранилища, их атрибуты и взаимосвязи, задавать физическую модель хранилища, представлять структуру хранилища в удобной графической форме;
- задавать доступ к внешним данным;
- описывать процедуры загрузки в хранилище и выполнять их;
- автоматически генерировать метаданные.
Техническая архитектура
Требования к техническим средствам определяются требованиями к информационной системе в целом. Окончательное решение всегда принимается руководством – от крайне пессимистического до крайне оптимистического:
- закрытое и законченное техническое и программное обеспечение (самая дешевая архитектура): возможности расширения системы отсутствуют, реинжиниринг требует практически полной переделки системы;
- закрытая система, ограниченные возможности расширения, требуется сложный реинжиниринг;
- открытая система, позволяющая развивать систему, но заранее сделана ставка на одного производителя, может быть сложный реинжиниринг;
- открытая система, позволяющая развивать систему и использовать различные аппаратные платформы, проблемы реинжиниринга практически отсутствуют.
Техническая архитектура зависит от масштабов системы и требований к ее производительности и надежности – серверные компоненты могут располагаться на одном компьютере или на нескольких.
Организационное обеспечение системы
Организационное обеспечение должно включать в себя: - организацию новых и реорганизацию существующих подразделений для обеспечения… - обучение пользователей – составление групп пользователей, программ и методик обучения, подготовка учебных материалов…Реализация и внедрение системы
Завершается физическое проектирование системы: - определяется необходимость распределения данных; - производится анализ использования данных;Оценка потенциальной емкости рынка и потенциального объема продаж
Потенциальный объем продаж системы: доля, которую система может получить на рынке товаров и услуг исходя из ее объективных технико-экономических… На эту долю влияют не только технико-экономические, но и другие факторы,… Для определения потенциального объема продаж товаров или услуг могут использоваться различные математические модели…Оценка конкурентоспособности
На первом этапе составляется общий список конкурентов и из него выбираются те, которые могут в принципе быть конкурентами рассматриваемой системы.… На втором этапе проводится анализ рассматриваемого проекта по сравнению с… Целью такого анализа является оценка того, насколько реальный (вероятный, прогнозируемый) объем продаж рассматриваемой…Метод определения чистой текущей стоимости.
Чистая текущая стоимость - NPV (net present value) - это разница между суммой поступлений от реализации проекта, приведенных к нулевому моменту… (9.1) Здесь I0 (investment) - первоначальное вложение средств (инвестиционные затраты); CFt (cash flow) - поступления…Метод расчета рентабельности инвестиций
Расчет этого показателя производится по формуле: (9.3) где I0 - первоначальные инвестиции, а CF - денежные поступления в году t, которые будут получены благодаря этим…Метод расчета внутренней нормы прибыли
Этот показатель также связан с NPV, а именно: IRR - это такое значение k в формулах (9.1) и (9.2), при котором NPV будет равно нулю. То есть, IRR -… Смысл расчета данного коэффициента при анализе эффективности инвестиций… Показатель, характеризующий уровень расходов, называется стоимостью авансированного капитала СС (cost of capital) либо…Расчет периода окупаемости инвестиций
Если величины денежных поступлений примерно равны по годам, формула расчета периода окупаемости имеет вид: (4.6) где РР - период окупаемости (лет);Задачи управления проектами
Управление проектом представляет собой организацию планирования, руководства, координации трудовых, финансовых и материально-технических ресурсов на… Проект и процесс его реализации трактуются как сложная система, в которой сам… Основу управления проектами составляет взгляд на проект как на изменение исходного состояния любой системы, связанное…Пример анализа на чувствительность экономической задачи
Первая задача:на сколько можно сократить или увеличить запасы ресурсов?
После нахождения оптимального решения представляется вполне логичным выяснить, как отразится на оптимальном решении изменение запасов ресурсов. Особенно важно проанализировать следующие два аспекта.
На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции?
На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции?
Вторая задача: увеличение объема какого из ресурсов наиболее выгодно?
Третья задача:в каких пределах допустимо изменение целевой функции?
Каков диапазон изменения целевой функции, при котором не происходит изменения оптимального решения?
Пример анализа чувствительности при анализе эффективности инвестиций.
1 Выбор ключевого показателя эффективности.
2 Выбор факторов, относительно которых разработчик инвестиционного проекта не имеет однозначного суждения (т. е. находится в состоянии неопределенности). Типичными являются следующие факторы:
капитальные затраты и вложения в оборотные средства,
рыночные факторы — цена товара и объем продажи,
компоненты себестоимости продукции,
время строительства и ввода в действие основных средств.
2 Установление номинальных и предельных (нижних и верхних) значений неопределенных факторов, выбранных на втором шаге процедуры. Предельных факторов может быть несколько, например  5% и
5% и  10% от номинального значения (всего четыре в данном случае)
10% от номинального значения (всего четыре в данном случае)
3 Расчет ключевого показателя для всех выбранных предельных значений неопределенных факторов.
4 Построение графика чувствительности для всех неопределенных факторов. Ниже приводится пример такого графика для трех факторов.
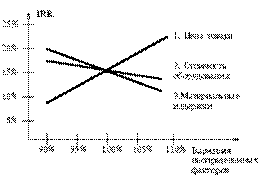
Чувствительность проекта к изменению неопределенных факторов
Данный график позволяет сделать вывод о наиболее критических факторах инвестиционного проекта, с тем чтобы в ходе его реализации обратить на эти факторы особое внимание с целью сократить риск реализации инвестиционного проекта. Так, например, если цена продукции оказалась критическим фактором, то в ходе реализации проекта необходимо улучшить программу маркетинга и (или) повысить качество товаров. Если проект окажется чувствительным к изменению объема производства, то следует уделить больше внимания совершенствованию внутреннего менеджмента предприятия и ввести специальные меры по повышению производительности. Наконец, если критическим оказался фактор материальных издержек, то целесообразно улучшить отношение с поставщиками, заключив долгосрочные контракты, позволяющие, возможно, снизить закупочную цену сырья.
· Шеннон: "Любой набор правил для разработки моделей в лучшем случае имеет ограниченную полезность и может служить лишь предположительно в качестве каркаса будущей модели или отправного пункта в ее построении".
· ** Один из фундаментальных приемов – бритва Оккама: "Не множь сущности без необходимости". (Не нужна модель прогноза погоды на один день, если с ней нужно работать два дня).
· Определение устойчивости по Ляпунову: движение устойчиво, если достаточно малые отклонения от него порождают траектории, которые остаются близкими к исходной траектории на достаточно большом интервале времени.
· Крылов А.Н.: "Сколько бы ни было точно математическое решение, оно не может быть точнее тех приближенных предпосылок, на коих оно основано. Об этом часто забывают, делают вначале какое-нибудь грубое приближенное предположение или допущение, часто даже не оговорив таковое, а затем придают полученной формуле гораздо большее доверие, нежели она заслуживает".
[1]Консервативные силы - силы поля, в котором работа, совершаемая над частицей силами поля, зависит лишь от начального и конечного положений частицы и не зависит от пути, по которому двигалась частица.
[2] Алгоритм в системном исследовании – предписание определенной последовательности неформализованных действий (в частности, творческой деятельности). В математике алгоритм – точное формальное предписание, однозначно определяющее содержание и последовательность действий (операций).
[3] Под методом обычно понимается некий унифицированный подход, с помощью которого ищутся пути решения поставленной задачи.
– Конец работы –
Используемые теги: методологические, основы, моделирования, сложных, систем0.061
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ МОДЕЛИРОВАНИЯ СЛОЖНЫХ СИСТЕМ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов