рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Векторная алгебра
Реферат Курсовая Конспект
Векторная алгебра
Векторная алгебра - раздел Философия, ВЫСШАЯ МАТЕМАТИКА Скалярным Произведением Двух Векторов Называется Число, Равное Произве...
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:
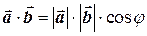 . (2.7)
. (2.7)
Скалярное произведение векторов обладает следующими свойствами:
10.  , ,
| 20.  , ,
|
30. 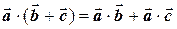 , ,
| 40.  . .
|
Отметим, что поскольку 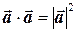 , то для скалярного квадрата используют обозначение
, то для скалярного квадрата используют обозначение  .
.
Пример 2.5. Вычислить выражение 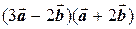 , если
, если  ,
, 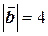 |, j=2p/3.
|, j=2p/3.
Решение. Раскроем скобки, учитывая свойства скалярного произведения векторов:
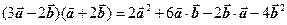 .
.
Далее из определения скалярного произведения следует:

 18–24–64 = –70.
18–24–64 = –70.
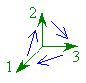
Тройка векторов называется правой, если вектора, приведенные к одному началу, располагаются также, как расставленные пальцы правой руки: большой палец – по первому вектору, указательный – по второму, средний – по третьему. Если смотреть во внутрь телесного угла, образованного этими векторами, то движение от первого ко второму, от второго к третьему будет совершаться против часовой стрелки. Обычно на практике рассматриваются только правые системы векторов.

| 
|
| Правая тройка | Левая тройка |
Векторным произведением вектора 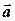 на вектор
на вектор 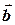 называется вектор
называется вектор 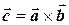 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
а) 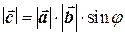 ,
,
б) вектор 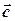 перпендикулярен к обоим векторам
перпендикулярен к обоим векторам 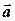 и
и 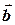 ,
,
в) упорядоченная тройка 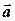 ,
, 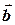 ,
, 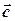 – правая.
– правая.
Векторное произведение векторов обладает следующими свойствами:
10.  , ,
| 20.  , ,
|
30. 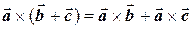 , ,
| 40. 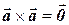 . .
|
Пример 2.6. Вычислить выражение  , если
, если  ,
, 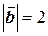 и j = 2p/3.
и j = 2p/3.
Решение. Раскроем скобки внутри модуля, учитывая свойства векторного произведения:
 .
.
Далее, из определения векторного произведения следует:
 .
.
Отметим еще некоторые свойства скалярного и векторного произведений:
Два вектора 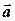 и
и 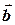 перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю:
перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю: 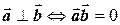 .
.
Два вектора 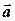 и
и 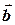 коллинеарны тогда и только тогда, когда их векторное произведение равно нулю:
коллинеарны тогда и только тогда, когда их векторное произведение равно нулю:  .
.
Если два вектора 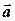 и
и 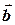 определены своими координатами в ортонормированном базисе:
определены своими координатами в ортонормированном базисе: 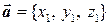 ,
,  , то скалярное произведение вычисляется по формуле:
, то скалярное произведение вычисляется по формуле:
 , (2.8)
, (2.8)
а векторное произведение по формуле
 (2.9)
(2.9)
Геометрический смысл векторного произведения: модуль векторного произведения  равен площади параллелограмма, построенного на этих векторах, как на сторонах.
равен площади параллелограмма, построенного на этих векторах, как на сторонах.
Смешанным произведением векторов 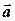 ,
, 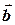 и
и 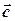 называется число
называется число  и обозначается
и обозначается 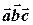 .
.
Смешанное произведение векторов обладает следующими свойствами:
10.  , ,
| 20. 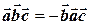 , ,
|
30. 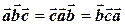 , ,
| 40.  . .
|
Отметим еще некоторые свойства смешанного произведения:
Три вектора 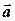 ,
, 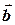 и
и 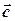 компланарны тогда и только тогда, когда их смешанное произведение равно нулю:
компланарны тогда и только тогда, когда их смешанное произведение равно нулю:
Если три вектора 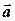 ,
, 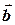 и
и 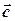 определены своими координатами в ортонормированном базисе:
определены своими координатами в ортонормированном базисе: 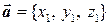 ,
,  ,
,  , то смешанное произведение вычисляется по формуле:
, то смешанное произведение вычисляется по формуле:
 (2.10)
(2.10)
Геометрический смысл смешанного произведения: модуль смешанного произведения  равен объёму параллелепипеда, построенного на этих векторах, как на сторонах.
равен объёму параллелепипеда, построенного на этих векторах, как на сторонах.
Пример 2.7. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, если A(3;–2;–4), B(–5;3;4), C(1;–3;2), D(4;1;–2).
Решение. Найдем координаты векторов  :
:
 .
.
а) Объем пирамиды ABCD вычислим по формуле:
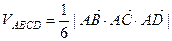 .
.
Поскольку
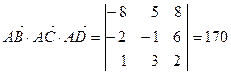 ,
,
то,

б) Площадь грани ABC вычислим по формуле:
 .
.
Поскольку
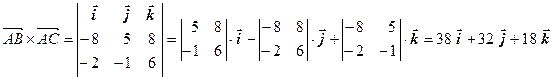 ,
,
то площадь грани ABC будет равна
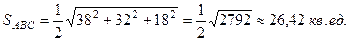
в) Для того чтобы найти косинус угла между ребрами AB и AC найдем косинус угла между векторами  и
и 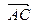 :
:
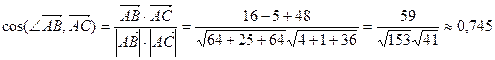 .
.
Тогда 
 .
.
– Конец работы –
Эта тема принадлежит разделу:
ВЫСШАЯ МАТЕМАТИКА
Сибирский государственный аэрокосмический университет... им академика М Ф Решетн ва...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Векторная алгебра
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов