рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Матричный метод. Обратная матрица
Реферат Курсовая Конспект
Матричный метод. Обратная матрица
Матричный метод. Обратная матрица - раздел Философия, ВЫСШАЯ МАТЕМАТИКА Матрица А–1 Называется Обратной Мат...
Матрица А–1 называется обратной матрицей по отношению к матрице А, если выполняется равенство AA–1 = A–1A = E. Только квадратные матрицы могут иметь обратные. Однако не каждая квадратная матрица имеет обратную. Для того чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля: detA¹0.
Пример 1.7. Решить систему линейных уравнений матричным методом (при помощи обратной матрицы).
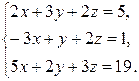
Решение. Запишем исходную систему уравнений в матричном виде:
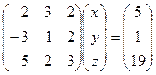 .
.
Тогда решение можно формально записать в виде:
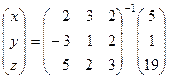 .
.
Таким образом, чтобы найти решение системы, нужно вычислить обратную матрицу
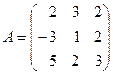 .
.
Найдем ее
1) Вычисляем определитель исходной матрицы: 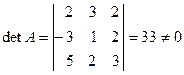 .
.
2) Транспонируем матрицу 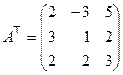 .
.
3) Находим все алгебраические дополнения транспонированной матрицы:
 , ,
| 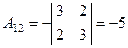 , ,
| 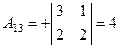 , ,
|
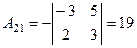 , ,
| 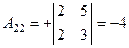 , ,
| 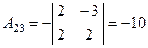 , ,
|
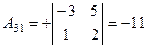 , ,
|  , ,
|  . .
|
4) Составляем присоединенную матрицу, для этого вместо элементов транспонированной матрицы ставим найденные алгебраические дополнения:
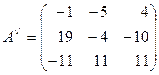
5) Записываем обратную матрицу, для этого все элементы присоединенной матрицы делим на определитель исходной матрицы:
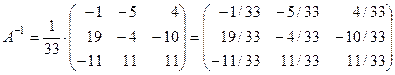 .
.
6) Сделаем проверку:
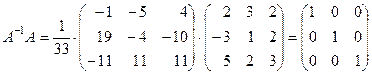 .
.
Следовательно, обратная матрица найдена правильно.
Теперь, используя найденную обратную матрицу можно найти решение исходной системы:
 .
.
– Конец работы –
Эта тема принадлежит разделу:
ВЫСШАЯ МАТЕМАТИКА
Сибирский государственный аэрокосмический университет... им академика М Ф Решетн ва...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Матричный метод. Обратная матрица
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов