рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Характеристика сил
Реферат Курсовая Конспект
Характеристика сил
Характеристика сил - раздел Механика, Механика – наука о движении и равновесии тел Сила В Общем Случае Зависит От Времени, Положения Точки И Скорости: ...
Сила в общем случае зависит от времени, положения точки и скорости:

Однако в ряде практических случаев сила оказывается функцией лишь одного из этих аргументов. Вместе с тем часто встречаются случаи, когда сила зависит от  , но практически её можно считать функцией лишь одной из этих переменных, т.к. остальные слабо влияют на движение. Познакомимся с некоторыми категориями сил.
, но практически её можно считать функцией лишь одной из этих переменных, т.к. остальные слабо влияют на движение. Познакомимся с некоторыми категориями сил.
1. СИЛЫ, ЗАВИСЯЩИЕ ТОЛЬКО ОТ ВРЕМЕНИ: 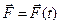
Со стороны электрического поля напряжённостью 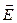 на точечный электрический заряд действует сила
на точечный электрический заряд действует сила 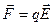 . Если напряжённость электрического поля зависит только от времени
. Если напряжённость электрического поля зависит только от времени  , то сила, действующая на точечный заряд, будет зависеть от времени:
, то сила, действующая на точечный заряд, будет зависеть от времени:
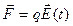
К силам этого класса, но действующим между материальными телами можно отнести, например, двигатель с возвратно-поступательным движением своих частей действует на фундамент. Во многих случаях такие силы имеют периодический характер и поэтому представляются тригонометрическими функциями.
2. СИЛЫ, ЗАВИСЯЩИЕ ТОЛЬКО ОТ СКОРОСТИ ТОЧКИ: 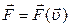
С такими силами мы чаще всего встречаемся тогда, когда рассматриваем движение тела в сопротивляющейся среде. Сила сопротивления со стороны среды возникает только тогда, когда имеется движение тела относительно среды. Когда относительная скорость обращается в нуль, сила сопротивления исчезает. Направлена эта сила противоположно скорости движения тела. Сила сопротивления зависит от скорости, эта зависимость в общем случае носит сложный характер. Однако, при медленном относительном движении тела силы сопротивления пропорционально скорости:
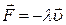 ,
,
где λ – коэффициент пропорциональности, зависящий от свойств среды ( в случае движения материальных тел λ зависит от формы и размеров тела). При более высоких скоростях движения такая зависимость оказывается неверной. В этом случае имеет место квадратичный или гидравлический закон сопротивления:
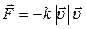 ,
,
где, k – коэффициент пропорциональности зависящий от тех же факторов, что и 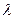 .
.
При очень больших скоростях движения этот закон становится более сложным, но с достаточной степенью точности можно считать, что сила сопротивления движению точки в жидкости или газе зависит только от скорости и направлена противоположно ей.
СИЛЫ, ЗАВИСЯЩИЕ ТОЛЬКО ОТ ПОЛОЖЕНИЯ ТОЧКИ: 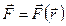
Особо важное значение имеют два типа сил этого класса: силы упругости и гравитационные силы.
а) СИЛЫ УПРУГОСТИ
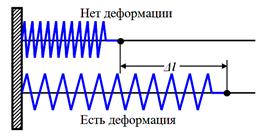 Силы упругости возникают при деформации упругих тел. Примером упругой силы может служить сила, возникающая при деформации пружины. Когда пружина находится в свободном состоянии – эта сила равна нулю. Но если пружину растянуть или сжать, то появляется сила, старающаяся вернуть её в первоначальное состояние.
Силы упругости возникают при деформации упругих тел. Примером упругой силы может служить сила, возникающая при деформации пружины. Когда пружина находится в свободном состоянии – эта сила равна нулю. Но если пружину растянуть или сжать, то появляется сила, старающаяся вернуть её в первоначальное состояние.
Для цилиндрической пружины 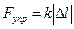 , где ∆l – удлинение, k – коэффициент пропорциональности – коэффициент жёсткости пружины.
, где ∆l – удлинение, k – коэффициент пропорциональности – коэффициент жёсткости пружины.
 Зависимость F ~ | l | не является обязательным признаком силы упругости (например, для конической пружины такая зависимость не является линейной.) Однако в большей части практических задач приходиться рассматривать упругую силу пропорциональную деформации.
Зависимость F ~ | l | не является обязательным признаком силы упругости (например, для конической пружины такая зависимость не является линейной.) Однако в большей части практических задач приходиться рассматривать упругую силу пропорциональную деформации.
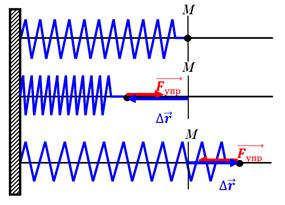 Точка закрепления N неподвижна относительно XYZ.
Точка закрепления N неподвижна относительно XYZ. 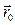 – радиус-вектор точки М при отсутствии деформации пружины
– радиус-вектор точки М при отсутствии деформации пружины  – радиус-вектор точки М при наличии деформации пружины. Для силы упругости
– радиус-вектор точки М при наличии деформации пружины. Для силы упругости  :
:
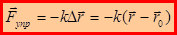 – закон Гука.
– закон Гука.
Знак «–» означает, что сила  направлена противоположно вектору
направлена противоположно вектору  .
.
Одно векторное уравнение, выражающее закон Гука, эквивалентно трем уравнениям в проекциях:
 – закон Гука.
– закон Гука.
Если положение точки М при отсутствии деформации совпадает с началом системы координат 0, предыдущие уравнения запишутся в виде:

Если с осью симметрии пружины совместить одну из осей декартовой системы координат (например, с осью 0X), мы получим одномерный случай для рассматриваемой задачи:
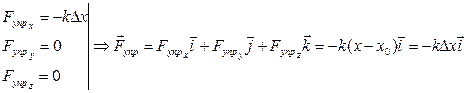
б) ГРАВИТАЦИОННЫЕ СИЛЫ
 Гравитационные силы – силы, определяемые законом всемирного тяготения, открытым И.Ньютоном (1678 г.): две материальные точки притягиваются друг к другу с силой пропорциональной массам этих материальных точек и обратно пропорциональной квадрату расстояние между ними:
Гравитационные силы – силы, определяемые законом всемирного тяготения, открытым И.Ньютоном (1678 г.): две материальные точки притягиваются друг к другу с силой пропорциональной массам этих материальных точек и обратно пропорциональной квадрату расстояние между ними:
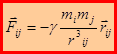 или
или  , где
, где  – вектор, проведенный от материальной точки массой mj к материальной точке массой mi,
– вектор, проведенный от материальной точки массой mj к материальной точке массой mi,  – радиус-вектор, определяемый положение точки пространства, в которой находится материальная точка массой mi ,
– радиус-вектор, определяемый положение точки пространства, в которой находится материальная точка массой mi , 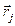 – радиус-вектор, определяемый положение точки пространства, в которой находится материальная точка массой mj,
– радиус-вектор, определяемый положение точки пространства, в которой находится материальная точка массой mj,  =6,67.10-11 Н.м2/кг2 – гравитационная постоянная (впервые определена в 1798 г. Генри Кавендишем.)
=6,67.10-11 Н.м2/кг2 – гравитационная постоянная (впервые определена в 1798 г. Генри Кавендишем.)
Гравитационная сила взаимодействия двух материальных тел определяется соотношением: 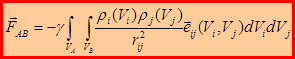
– Конец работы –
Эта тема принадлежит разделу:
Механика – наука о движении и равновесии тел
Основные понятия механики модели... Материальная точка геометрическая точка снабж нная массой имеющая... Системой отсчета называют тело отсчета жестко связанную с ним систему координат и часы...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Характеристика сил
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов