рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Строительство
- /
- ВНЕЦЕНТРЕННОЕ ДЕЙСТВИЕ ПРОДОЛЬНОЙ СИЛЫ
Реферат Курсовая Конспект
ВНЕЦЕНТРЕННОЕ ДЕЙСТВИЕ ПРОДОЛЬНОЙ СИЛЫ
ВНЕЦЕНТРЕННОЕ ДЕЙСТВИЕ ПРОДОЛЬНОЙ СИЛЫ - раздел Строительство, ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ 1. О П Р Е Д Е Л Е Н И Е Напряжений. Рассмотрим Случай Внецентренного Сжатия...
1. О п р е д е л е н и е напряжений. Рассмотрим случай внецентренного сжатия массивных колонн (рис. 288). Такая задача очень часто встречается в мостостроении при расчете опор мостов и в гражданском строительстве при расчете колонн зданий.
Предположим, что сжимающая сила Р приложена в точке с, которая имеет координаты хР и уР, отсчитанные относительно главных центральных осей инерции.
От этой силы в произвольном сечении стержня возникают нормальная сжимающая сила N = — Р и два изгибающих момента, которые
в соответствии с принятым правилом знаков будут отрицательными, так как они вызывают сжатие в точках, лежащих в первой четверти:
Мх = —РуР; Му = — РхР.
Напряжение в произвольной точке К, лежащей в положительной четверти произвольного поперечного сечения, равно

|
(11.10)
По формуле (11.10) можно найти напряжение в любой точке сжатой колонны; для этого необходимо величины хну брать с учетом знака.

|
|
Рассмотрим теперь частный случай внецентренного сжатия колонны прямоугольного сечения, когда один из эксцентриситетов равен нулю. Пусть сила расположена на оси Оу (хР = 0, уР = е), как это показано на рис. 289. Подставляя эти значения в формулу напряжений (11.10), для крайних волокон получим

Из этой формулы видно, что при е = О напряжения вс всем сече-нии одинаковые. Ьсли е <;-«-, то напряжения во всем сечении одного
знака (сжатие). В частности, когда e=-jr, напряжения в точках
А и В равны:
2Р вА = — -у-; ств=О.
_ ^ Ъ I __,
Если, наконец, е >■---, то нейтральная ось расположена внутри
сечения. Она разделит его на две части: в одной из них напряжения сжимающие, а в другой — растягивающие. Для этих четырех случаев на рис. 289 показаны эпюры напряжений. Таким образом, если не хо-1ят, чтобы в поперечном сечении появлялись растягивающие напряжения, то эксцентриситет нельзя допускать больше чем Ь/6.
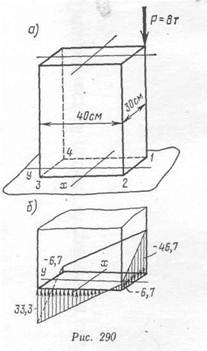
Пример. Определить напряжения и построить их эпюру в поперечном сечении колонны (рис. 290, а).
Найдем изгибающие моменты:
Мх = + 8000 • 20 = 160000 кгс ■ см; М^ = + 8000- 15 = 120000 кгс ■ см.
Найдем геометрические характеристики сечения: площадь сечения
F = 40- 30= 1200 см2; моменты сопротивления:
5^ = ^ = 8000 см'; о
40 • 302
Wu= =6000 см*. у 6
Найдем теперь напряжения в четырех угловых точках поперечного сечения: 8000 160000 120000 е_ оп. ОА.
°1==-ТЖ-^ооо--^ооо-:=-6'7-2О'о-2о'О=-4ь'7^'СЛ12:
о2 = — 6,7 — 20,0 + 20,0 = — 6,7 кгс/см*-, а3 = — 6,7 + 20,0 + 20,0 = 33,3 кгс/см^, о,, = — 6,7 + 20,0 — 20,0=— 6,7 кгфлР.
По этим значениям о построена эпюра напряжений (рис. 290, Щ.
2. Определение положения нулевой линии. Для того чтобы определить положение нулевой линии, преобразуем формулу (11.10). Подставляя в эту формулу значения моментов, получим
_ Р РуРУ Рхрх _ Р г, , уРу хрх -]
L {—) [—, J
Величины, стоящие в знаменателе второго и третьего слагаемых, представляют собой квадраты радиусов инерции сечения, т. е.
Следовательно,

Этой формулой, так же как и формулой (11.10), можно пользоваться для определения напряжений в любой точке поперечного сечения ко» лонны. Обозначим координаты любой точки нулевой линии Хх и ущ Если эти координаты подставить в уравнение (11.12) и учесть, что напряжения в точках нулевой линии равны нулю, то после сокращения на величину PIF получим уравнение нулевой линии
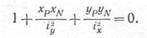
По этому уравнению можно определить отрезки, отсекаемые нулевой линией на осях координат. Обозначим эти отрезки (рис. 291, а) через


|
| Точно так же для случая у = 0, дгдг = ах имеем |

|
ах и ciy. Если положить хк — 0, ух — ау, то из уравнения (11.13) получим
Решая эти уравнения, получим отрезки, отсекаемые нейтральной линией на осях координат:

Вместе с тем можно решить обратную задачу, выразив координаты
точки приложения силы Р при заданных отрезках, отсекаемых нулевой
линией на осях координат: ч
*я = —-'"-; $>«=--—. (11.15)
 Отметим интересную зависимость величин хР и ах, а также уР и а,,. Если силу приложить в точке с координатами ах и ау, то нулевая линия отсечет отрезки на осях координат, равные соответственно Хр и у р. Если сила приложена в точке 1 (рис. 291, б), а соответствующая нулевая линия занимает положение /-/, то при силе, поставленной в точку 2, нулевая линия займет положение //-//.
Отметим интересную зависимость величин хР и ах, а также уР и а,,. Если силу приложить в точке с координатами ах и ау, то нулевая линия отсечет отрезки на осях координат, равные соответственно Хр и у р. Если сила приложена в точке 1 (рис. 291, б), а соответствующая нулевая линия занимает положение /-/, то при силе, поставленной в точку 2, нулевая линия займет положение //-//.
Рассмотрим теперь некоторые характерные особенности, связанные с поведением нулевой линии при различных положениях силы Р (рис. 292).


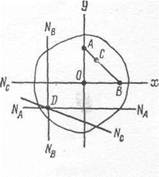
Рис. 293
Если сила Р приложена в точке, лежащей на оси Оу, то нулевая линия отсекает на оси Ох отрезок, равный бесконечности:
■ а* ~~ ~ ~хр~ ~ 0" ~ °°"
Это означает, что нулевая линия будет параллельна оси Ох.
Представим себе, что сила Р перемещается по оси Ох от центра тяжести к краю сечения. В этом случае нулевая линия перемещается из бесконечности по направлению к сечению, оставаясь при этом все время параллельной оси Оу. Точно так же если сила перемещается по оси Оу, то нулевая линия перемещается поступательно, оставаясь все время параллельной оси Ох.
Так, например, когда сила последовательно приложена в точках /, 2, 3, 4, (рис. 292), нулевая линия соответственно занимает положения /-/, //-//, ///-///, IV-IV и т. д.
Рассмотрим теперь случай, когда сила Р перемещается по некоторой прямой ОЕ, проходящей через центр тяжести сечения, но не совпадающей ни с одной из главных осей инерции. В этом случае нулевая линия (рис. 292) будет также перемещаться параллельно самой себе. В самом деле, из уравнений (11.14) вытекает соотношение

Отсюда можно сделать вывод, что тангенс угла наклона нулевой линии а„/аЛ не зависит от численного значения координат точки приложения силы, а зависит от их отношения.
Рассмотрим теперь еще одну задачу, которая имеет большое значение в дальнейших выводах. Пусть сила Р перемещается по некоторой прямой АВ, не проходящей через центр тяжести сечения (рис. 293). Для двух крайних случаев, когда сила приложена в точках А и В, нулевые линии параллельны соответствующим осям Ох и Оу. Пусть эти линии пересекаются в некоторой точке D. Так как эта точка принадлежит двум нулевым линиям, то напряжения в ней от двух сил, одновременно приложенных в точках А и В, равны нулю. Приложим теперь силу Р в точке С, лежащей на прямой А В. Эту силу можно разложить на две параллельные составляющие РА и Р;3, приложенные к точкам А и В. От этих двух составляющих, а" следовательно, и от их равнодействующей напряжения в точке D будут равню нулю. Так как точка С была взята произвольно, то при любом положении силы Р на прямой АВ напряжение в точке D равно нулю.
Отсюда можно сделать заключение, что при движении груза по прямой АВ нулевая линия вращается вокруг точки D.
Полученные в этом параграфе выводы о поведении нулевой линии, связанные с перемещением по сечению сжимающей силы, будут использованы для последующего анализа внецентренного сжатия колонн.
– Конец работы –
Эта тема принадлежит разделу:
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ
На сайте allrefs.net читайте: ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ВНЕЦЕНТРЕННОЕ ДЕЙСТВИЕ ПРОДОЛЬНОЙ СИЛЫ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов