рефераты конспекты курсовые дипломные лекции шпоры

Раздел Строительство
/
ПОНЯТИЕ 0 НОВЫХ ТЕОРИЯХ ПРОЧНОСТИ

Реферат Курсовая Конспект

Выберите учебное заведение

ПОНЯТИЕ 0 НОВЫХ ТЕОРИЯХ ПРОЧНОСТИ

ПОНЯТИЕ 0 НОВЫХ ТЕОРИЯХ ПРОЧНОСТИ - раздел Строительство, ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ Выше Были Изложены Основные Теории Прочности, Созданные За Длительный Период,...

Выше были изложены основные теории прочности, созданные за длительный период, начиная со второй половины XVII и до начала XX в.

Необходимо отметить, что помимо изложенных существует большое количество теорий, многие из которых не нашли достаточно широкого применения на практике.

За последнее время появились новые теории, которые главным образом связаны с новыми строительными материалами, в частности с пластмассами.

При построении приведенных в предыдущих параграфах теорий составлялись условия наступления предельного напряженного состояния, выраженные через главные напряжения а_ь а₂ и с₃.

Названные условия для каждой из рассмотренных теорий в общей форме могут быть записаны в виде функции

/(<*!, о₂, 0₃) = О. (а)

Например, условие (а), соответствующее энергетической теории, приобретает следующий вид:

f(Ou Щ, о₃) = °i + °i + ^а1 - ^СТЛ - о_го₃ - ст₂ст₃ - щ = 0. (б)

Построение новых теорий осуществляется путем отыскания и подбора такой функции (а), которая позволяла бы полнее учесть различные механические свойства материала, работающего в условиях сложного напряженного состояния.

Так, например, в одной из новых теорий, предложенной Ю. И. Яг-ном, функция (а) принимается в форме уравнения 2-й степени *:

(_Ol - а₂)² + (о₂ - а₃)² + К - ст₃)² + т {о, + а, + а₃)² +

+ п(о₁ + с₂ + в₃) = 1. (12.25)

Коэффициенты т, л и /в уравнении (12.25) должны определяться на основании трех опытов: при растяжении, сжатии и кручении (чистый сдвиг).

В результате указанных опытов находят предельные напряжения и с учетом принятого коэффициента запаса допускаемые напряжения

* Здесь сохранена форма изложения Ю. И. Ягна, который исходил из метода допускаемых напряжений.

[а,,1, [а_с] и [т_к]. Используя уравнение (12.25) отдельно для растяжения о, = [ст_р], а₂ = ст₃ — 0. Д-1Я сжатия о_г — 0, а₂ — — [а_с1, ст₃ = 0 и для кручения а_х = — а, — [tJ, а₃ = 0, получают три уравнения:

Из совместного решения уравнений (12.26) находят следующие значения коэффициентов:

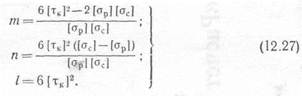
Подставляя найденные коэффициенты в уравнение (12.25), получают следующее условие:

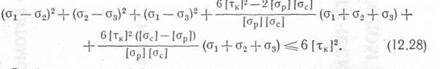
Особенность данной теории состоит в том, что она, так же как и теория Мора, позволяет учитывать неодинаковое сопротивление материала растяжению и сжатию и одновременно с этим учитывает сопротивление материала сдвиг)'.

Следует заметить, что если в условие (12.28) подставить значение о_т из выражения (12.22)

Ы-Ш-ЫУЗ. (12.29)

то после несложных преобразований получим условие (12.18), отвечающее энергетической теории, которая, таким образом, является как бы частным случаем теории Ю. И. Ягна.

Данная теория еще недостаточно проверена опытами.

При построении теорий прочности для пластмасс и, в частности, для слоистых пластмасс и стеклопластиков, которые могут быть отнесены к анизотропным материалам, в функцию (а) также вводятся коэффициенты, определяемые на основании опытов.

Характерным здесь является то обстоятельство, что элементы слоистых пластмасс, и, в частности, стеклопластика, находящиеся в условиях одного и того же напряженного состояния (рис. 307), но с различной ориентировкой стекловолокон (слоев), не будут равнопрочны. В случае, показанном на рис. 307, а, растяжению будут подвергаться стекловолокна, а сжатию — связующая масса, в случае же, показанном на рис. 307, б, наоборот, стекловолокна будутсжаты, а связующая масса растянута. Прочность же этих двух материалов неодинакова при растяжении и сжатии. Сопротивление стеклопластика, армиро-

ванного стекловолокнами только в одном направлении, оказывается, зависит не только от величины, но н от направления касательных напряжений. Это легко понять из рис. 307, в, г. Так, например, при случае действия касательных напряжений, как показано на рис. 307, в, стекловолокна, направленные по диагонали тп, растягиваются, а при изменении направления действия г (рис. 307, г) те же волокна сжаты. В первом случае хорошо работающие на растяжение волокна повышают прочность материала, а во втором они почти не оказывают влияния на прочность так как плохо работают на сжатие.

Указанные выше особенности сопротивления стеклопластиков учитываются при составлении уравнения (а), в которое вводится необходимое количество констант, определяемых экспериментальным путем.

Так, для стеклопластика, работающего в условиях плоского напряженного состояния, требуется предварительно найти семь констант.

Следует заметить, что пост-

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ

На сайте allrefs.net читайте: ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ПОНЯТИЕ 0 НОВЫХ ТЕОРИЯХ ПРОЧНОСТИ

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

ОБЩИЕ ЗАМЕЧАНИЯ
Для того чтобы судить о работе изгибаемых балок; недостаточно знать только напряжения, которые возникают в сечениях балки от заданной нагрузки. Вычисленные напряжения позволяют проверить п

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ОСИ ИЗОГНУТОГО БРУСА
При выводе формулы нормальных напряжений при изгибе (см. § 62) была получена связь между кривизной и изгибающим моментом: 1 VI Формула (9.3) показывает, что кривизна изменяется по

Do , С М , ■. п , .
di=*±)irjdz + C- <а) Это выражение определяет закон изменения углов поворота касательной по длине балки.

МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ
Задача определения прогибов может быть значительно упрощена, если применять т

З - ei • а
Здесь v ■— прогиб в произвольном сечении первого участка; М — функция,выражающая значение изгибающего момента в произвольном сечении первого

Г J д- J у
* В отдельных случаях, когда стержень обладает мал

ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ СТЕРЖНЯ С ЛОМАНОЙ ОСЬЮ
При проектировании машин часто приходится рассчитывать брус, ось которого пре

КОСОЙ ИЗГИБ
Косым изгибом называется такой случай изгиба бруса, при котором плоскость действия суммарного изгибающего момента в сечении не совпадает ни с одной из главных осей инерции. Короче говоря, в

ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ ИЗГИБА И ПРОДОЛЬНОЙ СИЛЫ
Очень многие стержни сооружений и машин работают одновременно как на изгиб, так и на растяжение или сжатие. Простейший случай показан на рис. 285, когда на колонну действует нагрузка, вызывающая в

Gt; х J у
Пользуясь этой формулой, можно определить напряжение в любой точке и найти наибольшее напряжение в данном поперечном сечении. Если поперечное сечение стержня имеет простую форму, напр

ВНЕЦЕНТРЕННОЕ ДЕЙСТВИЕ ПРОДОЛЬНОЙ СИЛЫ
1. О п р е д е л е н и е напряжений. Рассмотрим случай внецентренного сжатия массивных колонн (рис. 288). Такая задача очень часто встречается в мостостроении при расчете опор мостов и в гражданск

ЯДРО СЕЧЕНИЯ
Рассмотрим случай внецентренного сжатия массивной колонны произвольного поперечного сечения. Предположим, что сила Р перемещается из центра тяжести поперечного сечения по прямой ОА (

ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ КРУЧЕНИЯ С ИЗГИБОМ
Одновременное действие кручения с изгибом чаще всего встречается в различных деталях машин. Например, коленчатый вал воспринимает значительные крутящие моменты и, кроме того, работает на изгиб. Оси

ОСНОВНЫЕ ПОЛОЖЕНИЯ
При оценке прочности различных конструкций и машин часто приходится учитывать, что многие их элементы и детали работают в условиях сложного напряженного состояния. В гл. III было установ

ЭНЕРГЕТИЧЕСКАЯ ТЕОРИЯ ПРОЧНОСТИ
Энергетическая теория основывается на предположении о том, что количество удельной потенциальной энергии деформации, накопленной к моменту наступления предельного напряженного состояния в мате

О + О2 /О —О 2
]/ (^) () т^««. (12.19) Для частного случая при оу = 0, положив az — а и хгу = т, имеем VW. (12.20) Энергетическая т

ТЕОРИЯ ПРОЧНОСТИ МОРА
Во всех рассмотренных выше теориях в качестве гипотезы, устанавливающей причину наступления предельного напряженного состояния, принималась величина какого-либо одного фактора, например напряжен

ОБЪЕДИНЕННАЯ ТЕОРИЯ ПРОЧНОСТИ
В данной теории различают два вида разрушения материала: хрупкое, которое происходит путем отрыва, и вязкое, наступаю щее от среза (сдвига) *. __________________________________

ОСНОВНЫЕ ПОНЯТИЯ
Тонкостенными называют стержни, длина которых значительно превышает основные размеры b или h поперечного сечения (в 8— 10 раз), а последние, в свою очередь, значительно превосх

СВОБОДНОЕ КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
Свободным кручением называется такое кручение, при котором депланация всех поперечных сечений стержня будет одинаковой. Так, на рис. 310, а, б показан стержень, нагруженный н

Т - М" А /пи
Угол закручивания полосы находится из выражения d В формулах (13.1) и (13.2) о

ОБЩИЕ ЗАМЕЧАНИЯ
, В строительной практике и в особенности в машиностроении часто встречаются стержни (брусья) с криволинейной осью. На рис. 339

РАСТЯЖЕНИЕ И СЖАТИЕ КРИВОГО БРУСА
В отличие от прямого бруса внешняя сила, приложенная нормально к какому-либо

ЧИСТЫЙ ИЗГИБ КРИВОГО БРУСА
Для определения напряжений при чистом изгибе плоского кривого бруса, так же как для прямого бруса, считаем справедливой гипотезу плоских сечений. Определяя деформации волокон бруса, пренебрегаем н

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ В КРИВОМ БРУСЕ ПРИ ЧИСТОМ ИЗГИБЕ
Для вычисления напряжений по формуле (14.6), полученной в предыдущем параграфе, необходимо знать, как проходит нейтральная ось. Для этой цели надо определить радиус кривизны нейтрального слоя г

НАПРЯЖЕНИЕ ПРИ ОДНОВРЕМЕННОМ ДЕЙСТВИИ ПРОДОЛЬНОЙ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА
Если в сечении кривого бруса одновременно возникают изгибающий момент и продольная сила, то напряжение следует определять как сумму напряжений от двух указанных воздействий:

Т F *? "л 99 R f Q ft " Ч

МЕТОД ЭЙЛЕРА ДЛЯ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКИХ СИЛ. ВЫВОД ФОРМУЛЫ ЭЙЛЕРА
Для исследования устойчивости равновесия упругих систем имеется несколько методов. Основы и техника применения этих методов изучаются в специальных курсах, посвященных проблемам устойчивости разли

СТЕРЖНЯ НА ВЕЛИЧИНУ КРИТИЧЕСКОЙ СИЛЫ
На рис. 358 показаны различные случаи закрепления концов сжатого стержня. Для каждой из этих зада*ч необходимо проводить свое решение аналогично тому, как это сделано в предыдущем параграфе для ша