рефераты конспекты курсовые дипломные лекции шпоры

Раздел Строительство
/
ТЕОРИЯ ПРОЧНОСТИ МОРА

Реферат Курсовая Конспект

Выберите учебное заведение

ТЕОРИЯ ПРОЧНОСТИ МОРА

ТЕОРИЯ ПРОЧНОСТИ МОРА - раздел Строительство, ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ Во Всех Рассмотренных Выше Теориях В Качестве Гипотезы, Устанавливающей Прич...

Во всех рассмотренных выше теориях в качестве гипотезы, устанавливающей причину наступления предельного напряженного состояния, принималась величина какого-либо одного фактора, например напряжения, удлинения, энергии.

В теории Мора в отличие от изложенных теорий не рассматриваются отдельные гипотезы, а на основе экспериментальных данных устанавливается определенная зависимость прочностных свойств материала от вида напряженного состояния. Для получения и обоснования такой зависимости используют предложенные Мором круги напряжений. Для объемного напряженного состояния, как известно, строят три круга

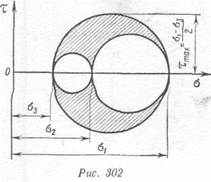
(рис. 302). Однако здесь на основе имеющихся опытов не учитывают влияние напряжений о₂ * и считают с некоторым приближением, что прочностные свойства материала связаны только с напряжениями о, и а₃. Поэтому из трех кругов рассматривают лишь один, а именно наибольший. Этот круг Мор назвал главным кругом.

В случае, когда напряжения Qfj и а₃ отвечают предельному напряженному состоянию главный круг принято называть

материала, соответствующий им также предельным.

В качестве примера на рис. 303 изображены три предельных круга для материала, который был испытан на растяжение, сжатие и кручение. При этом предельные напряжения при сжатии, которые будем

обозначать о_ос, оказались больше, чем при растяжении а_ор, т. е.

о_ос > ^ао_Р-

Если провести огибающую для этих кругов, которую называют предельной огибающей, то в общем случае она будет кривой, которая пересечет ось 0 в некоторой точке _ЧС

* Опыты показывают, что ошибка от неучета напряжения о₂ не превышает 10—15%.

Эта точка соответствует всестороннему растяжению с предельным напряжением, определяемым абсциссой точки С (см. рис. 303). Круг Мора в этом случае обращается в точку, ввиду того что напряжения а_ь а₂ и а₃ равны между собой.

Таким образом, если имеется, несколько предельных кругов и их огибающая, то можно принять, что напряженное состояние, главный круг которого касается огибающей, будет также предельным.

На рис. 303 изображено пунктиром семейство предельных кругов с различными сочетаниями главных напряжений. Как видно из рисунка, огибающая кругов определяет зависимость этих напряжений от вида напряженного состояния.

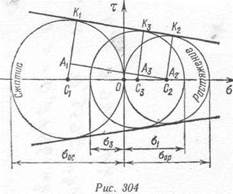
Получение действительной огибающей предельных кругов, построенных для всевозможных напряженных состояний, неосуществимо, так как для этого потребовалось бы опытным путем исследовать указанные напряженные состояния. Поэтому на практике действительную огибающую заменяют прямыми, касательными лишь к двум главным кругам, которые строят по данным опыта на растяжение и сжатие (рис. 304). Эти прямые являются границами области прочностных состояний. Вместе с тем они устанавливают линейную зависимость между напряжениями о, и а₃ всякого напряженного состояния, главный круг которого касается этих прямых:

0! = fl + to₃. (12.23)

Зависимость (12.23) получается на основе простых геометрических соотношений, вытекающих из подобия треугольников Л А₃С_яС_г и Д А_ХС_ХС₂ (рис. 304). Рассматривая эти треугольники, можно записать

где

Подстановка значений (б) в выражение (а) приводит после несложных преобразований к выражению (12.23). Так как последнее должно быть справедливо и для случаев растяжения и сжатия, то можно определить коэффициенты а и b для произвольного сочетания с?! и а₃

не прибегая к указанному преобразованию.

Так, при растяжении о₃ = 0, а °i " ^ао_Р- Введя эти значения напряжений в выражение (12.23), найдем, что а = а_ор.

При сжатии о₁ = 0 и о₃ = — о_ос. Следовательно, имеем

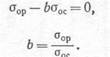
откуда

(в) (г) (12.24)

Таким образом, выражение (12.23) принимает следующий вид:

или

Соответствующая расчетная формула запишется так:

^сграсч = ^а1 — Ko₃s^R,

где R — расчетное сопротивление при растяжении.

Коэффициент К позволяет учитывать различные сопротивления материала растяжению и сжатию. Если эти сопротивления одинаковы по величине, то коэффициент К = 1, а касательные к главным кругам становятся параллельными оси а (рис. 305). Условие (12.24) в этом случае будет таким же, как и для третьей теории прочности. Следовательно, оно применимо как для хрупких, так и для пластичных материалов. При этом для хрупких материалов вместо ст_ор и 0_ОС берутся соответствующие пределы прочности, а для пластичных — пределы текучести.

В заключение следует отметить, что теория Мора дает наиболее достоверные результаты для напряженных состояний, круги которых занимают положение в промежутке между главными кругами растяжения и сжатия.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ

На сайте allrefs.net читайте: ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ТЕОРИЯ ПРОЧНОСТИ МОРА

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

ОБЩИЕ ЗАМЕЧАНИЯ
Для того чтобы судить о работе изгибаемых балок; недостаточно знать только напряжения, которые возникают в сечениях балки от заданной нагрузки. Вычисленные напряжения позволяют проверить п

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ОСИ ИЗОГНУТОГО БРУСА
При выводе формулы нормальных напряжений при изгибе (см. § 62) была получена связь между кривизной и изгибающим моментом: 1 VI Формула (9.3) показывает, что кривизна изменяется по

Do , С М , ■. п , .
di=*±)irjdz + C- <а) Это выражение определяет закон изменения углов поворота касательной по длине балки.

МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ
Задача определения прогибов может быть значительно упрощена, если применять т

З - ei • а
Здесь v ■— прогиб в произвольном сечении первого участка; М — функция,выражающая значение изгибающего момента в произвольном сечении первого

Г J д- J у
* В отдельных случаях, когда стержень обладает мал

ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ СТЕРЖНЯ С ЛОМАНОЙ ОСЬЮ
При проектировании машин часто приходится рассчитывать брус, ось которого пре

КОСОЙ ИЗГИБ
Косым изгибом называется такой случай изгиба бруса, при котором плоскость действия суммарного изгибающего момента в сечении не совпадает ни с одной из главных осей инерции. Короче говоря, в

ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ ИЗГИБА И ПРОДОЛЬНОЙ СИЛЫ
Очень многие стержни сооружений и машин работают одновременно как на изгиб, так и на растяжение или сжатие. Простейший случай показан на рис. 285, когда на колонну действует нагрузка, вызывающая в

Gt; х J у
Пользуясь этой формулой, можно определить напряжение в любой точке и найти наибольшее напряжение в данном поперечном сечении. Если поперечное сечение стержня имеет простую форму, напр

ВНЕЦЕНТРЕННОЕ ДЕЙСТВИЕ ПРОДОЛЬНОЙ СИЛЫ
1. О п р е д е л е н и е напряжений. Рассмотрим случай внецентренного сжатия массивных колонн (рис. 288). Такая задача очень часто встречается в мостостроении при расчете опор мостов и в гражданск

ЯДРО СЕЧЕНИЯ
Рассмотрим случай внецентренного сжатия массивной колонны произвольного поперечного сечения. Предположим, что сила Р перемещается из центра тяжести поперечного сечения по прямой ОА (

ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ КРУЧЕНИЯ С ИЗГИБОМ
Одновременное действие кручения с изгибом чаще всего встречается в различных деталях машин. Например, коленчатый вал воспринимает значительные крутящие моменты и, кроме того, работает на изгиб. Оси

ОСНОВНЫЕ ПОЛОЖЕНИЯ
При оценке прочности различных конструкций и машин часто приходится учитывать, что многие их элементы и детали работают в условиях сложного напряженного состояния. В гл. III было установ

ЭНЕРГЕТИЧЕСКАЯ ТЕОРИЯ ПРОЧНОСТИ
Энергетическая теория основывается на предположении о том, что количество удельной потенциальной энергии деформации, накопленной к моменту наступления предельного напряженного состояния в мате

О + О2 /О —О 2
]/ (^) () т^««. (12.19) Для частного случая при оу = 0, положив az — а и хгу = т, имеем VW. (12.20) Энергетическая т

ОБЪЕДИНЕННАЯ ТЕОРИЯ ПРОЧНОСТИ
В данной теории различают два вида разрушения материала: хрупкое, которое происходит путем отрыва, и вязкое, наступаю щее от среза (сдвига) *. __________________________________

ПОНЯТИЕ 0 НОВЫХ ТЕОРИЯХ ПРОЧНОСТИ
Выше были изложены основные теории прочности, созданные за длительный период, начиная со второй половины XVII и до начала XX в. Необходимо отметить, что помимо изложенных существует большо

ОСНОВНЫЕ ПОНЯТИЯ
Тонкостенными называют стержни, длина которых значительно превышает основные размеры b или h поперечного сечения (в 8— 10 раз), а последние, в свою очередь, значительно превосх

СВОБОДНОЕ КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
Свободным кручением называется такое кручение, при котором депланация всех поперечных сечений стержня будет одинаковой. Так, на рис. 310, а, б показан стержень, нагруженный н

Т - М" А /пи
Угол закручивания полосы находится из выражения d В формулах (13.1) и (13.2) о

ОБЩИЕ ЗАМЕЧАНИЯ
, В строительной практике и в особенности в машиностроении часто встречаются стержни (брусья) с криволинейной осью. На рис. 339

РАСТЯЖЕНИЕ И СЖАТИЕ КРИВОГО БРУСА
В отличие от прямого бруса внешняя сила, приложенная нормально к какому-либо

ЧИСТЫЙ ИЗГИБ КРИВОГО БРУСА
Для определения напряжений при чистом изгибе плоского кривого бруса, так же как для прямого бруса, считаем справедливой гипотезу плоских сечений. Определяя деформации волокон бруса, пренебрегаем н

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ В КРИВОМ БРУСЕ ПРИ ЧИСТОМ ИЗГИБЕ
Для вычисления напряжений по формуле (14.6), полученной в предыдущем параграфе, необходимо знать, как проходит нейтральная ось. Для этой цели надо определить радиус кривизны нейтрального слоя г

НАПРЯЖЕНИЕ ПРИ ОДНОВРЕМЕННОМ ДЕЙСТВИИ ПРОДОЛЬНОЙ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА
Если в сечении кривого бруса одновременно возникают изгибающий момент и продольная сила, то напряжение следует определять как сумму напряжений от двух указанных воздействий:

Т F *? "л 99 R f Q ft " Ч

МЕТОД ЭЙЛЕРА ДЛЯ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКИХ СИЛ. ВЫВОД ФОРМУЛЫ ЭЙЛЕРА
Для исследования устойчивости равновесия упругих систем имеется несколько методов. Основы и техника применения этих методов изучаются в специальных курсах, посвященных проблемам устойчивости разли

СТЕРЖНЯ НА ВЕЛИЧИНУ КРИТИЧЕСКОЙ СИЛЫ
На рис. 358 показаны различные случаи закрепления концов сжатого стержня. Для каждой из этих зада*ч необходимо проводить свое решение аналогично тому, как это сделано в предыдущем параграфе для ша