рефераты конспекты курсовые дипломные лекции шпоры

Раздел Строительство
/
ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ СТЕРЖНЯ С ЛОМАНОЙ ОСЬЮ

Реферат Курсовая Конспект

Выберите учебное заведение

ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ СТЕРЖНЯ С ЛОМАНОЙ ОСЬЮ

ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ СТЕРЖНЯ С ЛОМАНОЙ ОСЬЮ - раздел Строительство, ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ ...

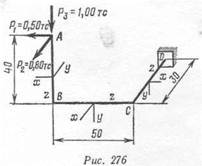
При проектировании машин часто приходится рассчитывать брус, ось которого представляет собой пространственную линию, состоящую из отрезков прямых. Так, например, на рис. 276 показан брус, состоящий из трех стержней: АВ, ВС и CD. Два первых стержня лежат г. одной плоскости, а стержень CD расположен в плоскости, нормальной к первой.

Расчет таких стержней начинается с определения внутренних силовых факторов в ряде сечений. Для отыскания наиболее напряженного (опасного) сечения строятся эпюры силовых факторов

N, М,, М_у, М„ Q.v, Q_y.

В первую очередь необходимо для каждого из стержней назначить

оси координат. Обычно ось, совпадающую с осью бруса, обозначают осью Oz, а две другие оси совмещают с главными осями инерции сечения.

Эпюры моментов и поперечных сил для каждого стержня строят, как для плоского бруса, с применением (для моментов) принятого ранееправила знаков (см. стр. 168). При этом мысленно располагают каждый из стержней по отношению к себе так, чтобы взор был направлен в начало координат со стороны положительной оси Ох (при построении эпюр Qy и М_х) или оси Оу (при построении эпюр Q_x и М_у). Рассмотрим пример построения эпюр для бруса, изображенного на рис. 276, когда на него действуют три силы:

Р_х = 0,50 тс; Р₂ = 0,80 тс и Я₃= 1,00тс.

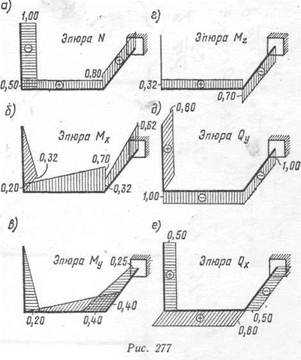
На рис. 277 показаны эпюры нормальных сил N, изгибающих моментов М_х и М_у, крутящего момента M_z и поперечных сил Q_y и Q_x. Эти эпюры построены на основании вычисленных значений ординат для сечений, расположенных по концам каждого стержня. Крутящий момент будем считать положительным, если при взгляде на отсеченную часть со стороны сечения будет установлено, что момент М_г стремится повернуть сечение по ходу часовой стрелки.

Наиболее просто строится эпюра нормальных сил N. Рассекая стержень плоскостью, нормальной к его оси, и рассматривая равновесие отсеченной части, к которой приложены внешние силы, легко определить значение нормальной силы. Для этого необходимо спроектировать все силы на ось соответствующего стержня и из уравнения 2z=0 определить силу N. Эпюра N показана на рис. 277, а.

Несколько сложнее определяются изгибающие моменты. Рассмотрим подробнее вычисление изгибающих моментов М_х. В стержне АВ изгиб относительно оси х вызывает только одна сила P_t, поэтому эпюра моментов имеет вид треугольника. Наибольший момент будет в нижнем сечении, проведенном через точку В. Так как через эту точку можно провести два сечения, одно из которых относится к вертикальному стержню, а другое — к горизонтальному, то в дальнейшем обозначим момент буквой М с двумя дополнительными индексами вверху. Первый верхний индекс показывает точку, через которую проведено сечение, а два индекса вместе определяют стержень, для которого находится изгибающий момент. Например, М_х^а — момент относительно оси х в сечении, проведенном в точке В, но относящимся к стержню В А; М_х ■— момент в сечении В, проведенном вертикальной плоскостью в стержне ВС. Длины стержней обозначим буквой / также с двумя индексами, определяющими концевые сечения стержня, например 1_аЬ, 1_Ьс и т. п.

Таким образом, имеем: для стержня АВ

М^ь_х^а = Р4сь = 0,80 0,40 = 0,32 тс; для стержня ВС

М_х^с = — PJab — — 0,50-0,40= —0,20 тс-м (растянутое волокно вверху); в точке С момент относительно оси х создают две силы:

M^c_x^b = -P₁l_ab-P₃l_bc=-0,50 0,40 -1,00 -0,50 = -0,70 тс-м; для стержня CD ■

М^с_х = — Р4аъ = — 0,80 • 0,40 = — 0,32 тс ■ м;

M^d_x = — P₂U - P4cd = — 0,8 ■ 0,4 - 1,00 • 0,30 = — 0,62 тс ■ м.

По этим данным построена эпюра М_х, которая показана на рис. 277, б.

Аналогичным образом построена эпюра М_и (рис. 277, б). Более просто вычисляются крутящие моменты. В стержне АВ крутящий момент равен нулю. В стержне ВС

М^ь_г^с = /у_ай = 0,32 тс-м, а в стержне CD

М^сг - — /У«* - P₃t_bc - - 0,70 тс ■ м.

По этим данным построена эпюра крутящих моментов (рис. 277, г).

Поперечные силы Q_x и Q_y определяют как сумму проекций на оси х и у всех сил, действующих на отсеченную часть.

В соответствии с принятыми выше правилами знаков найдены поперечные силы в стержнях и по ним построены эпюры, показанные на рис. 277, д, е.

В зависимости от размеров и формы сечений для каждого элемента бруса по формуле (а) предыдущего параграфа можно определить нормальные напряжения и построить эпюру а в заданном сечении: Суммарные касательные напряжения от двух поперечных сил Q_y и Q_x, а также от крутящего момента М_г должны быть получены путем геометрического суммирования.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ

На сайте allrefs.net читайте: ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ СТЕРЖНЯ С ЛОМАНОЙ ОСЬЮ

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

ОБЩИЕ ЗАМЕЧАНИЯ
Для того чтобы судить о работе изгибаемых балок; недостаточно знать только напряжения, которые возникают в сечениях балки от заданной нагрузки. Вычисленные напряжения позволяют проверить п

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ОСИ ИЗОГНУТОГО БРУСА
При выводе формулы нормальных напряжений при изгибе (см. § 62) была получена связь между кривизной и изгибающим моментом: 1 VI Формула (9.3) показывает, что кривизна изменяется по

Do , С М , ■. п , .
di=*±)irjdz + C- <а) Это выражение определяет закон изменения углов поворота касательной по длине балки.

МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ
Задача определения прогибов может быть значительно упрощена, если применять т

З - ei • а
Здесь v ■— прогиб в произвольном сечении первого участка; М — функция,выражающая значение изгибающего момента в произвольном сечении первого

Г J д- J у
* В отдельных случаях, когда стержень обладает мал

КОСОЙ ИЗГИБ
Косым изгибом называется такой случай изгиба бруса, при котором плоскость действия суммарного изгибающего момента в сечении не совпадает ни с одной из главных осей инерции. Короче говоря, в

ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ ИЗГИБА И ПРОДОЛЬНОЙ СИЛЫ
Очень многие стержни сооружений и машин работают одновременно как на изгиб, так и на растяжение или сжатие. Простейший случай показан на рис. 285, когда на колонну действует нагрузка, вызывающая в

Gt; х J у
Пользуясь этой формулой, можно определить напряжение в любой точке и найти наибольшее напряжение в данном поперечном сечении. Если поперечное сечение стержня имеет простую форму, напр

ВНЕЦЕНТРЕННОЕ ДЕЙСТВИЕ ПРОДОЛЬНОЙ СИЛЫ
1. О п р е д е л е н и е напряжений. Рассмотрим случай внецентренного сжатия массивных колонн (рис. 288). Такая задача очень часто встречается в мостостроении при расчете опор мостов и в гражданск

ЯДРО СЕЧЕНИЯ
Рассмотрим случай внецентренного сжатия массивной колонны произвольного поперечного сечения. Предположим, что сила Р перемещается из центра тяжести поперечного сечения по прямой ОА (

ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ КРУЧЕНИЯ С ИЗГИБОМ
Одновременное действие кручения с изгибом чаще всего встречается в различных деталях машин. Например, коленчатый вал воспринимает значительные крутящие моменты и, кроме того, работает на изгиб. Оси

ОСНОВНЫЕ ПОЛОЖЕНИЯ
При оценке прочности различных конструкций и машин часто приходится учитывать, что многие их элементы и детали работают в условиях сложного напряженного состояния. В гл. III было установ

ЭНЕРГЕТИЧЕСКАЯ ТЕОРИЯ ПРОЧНОСТИ
Энергетическая теория основывается на предположении о том, что количество удельной потенциальной энергии деформации, накопленной к моменту наступления предельного напряженного состояния в мате

О + О2 /О —О 2
]/ (^) () т^««. (12.19) Для частного случая при оу = 0, положив az — а и хгу = т, имеем VW. (12.20) Энергетическая т

ТЕОРИЯ ПРОЧНОСТИ МОРА
Во всех рассмотренных выше теориях в качестве гипотезы, устанавливающей причину наступления предельного напряженного состояния, принималась величина какого-либо одного фактора, например напряжен

ОБЪЕДИНЕННАЯ ТЕОРИЯ ПРОЧНОСТИ
В данной теории различают два вида разрушения материала: хрупкое, которое происходит путем отрыва, и вязкое, наступаю щее от среза (сдвига) *. __________________________________

ПОНЯТИЕ 0 НОВЫХ ТЕОРИЯХ ПРОЧНОСТИ
Выше были изложены основные теории прочности, созданные за длительный период, начиная со второй половины XVII и до начала XX в. Необходимо отметить, что помимо изложенных существует большо

ОСНОВНЫЕ ПОНЯТИЯ
Тонкостенными называют стержни, длина которых значительно превышает основные размеры b или h поперечного сечения (в 8— 10 раз), а последние, в свою очередь, значительно превосх

СВОБОДНОЕ КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
Свободным кручением называется такое кручение, при котором депланация всех поперечных сечений стержня будет одинаковой. Так, на рис. 310, а, б показан стержень, нагруженный н

Т - М" А /пи
Угол закручивания полосы находится из выражения d В формулах (13.1) и (13.2) о

ОБЩИЕ ЗАМЕЧАНИЯ
, В строительной практике и в особенности в машиностроении часто встречаются стержни (брусья) с криволинейной осью. На рис. 339

РАСТЯЖЕНИЕ И СЖАТИЕ КРИВОГО БРУСА
В отличие от прямого бруса внешняя сила, приложенная нормально к какому-либо

ЧИСТЫЙ ИЗГИБ КРИВОГО БРУСА
Для определения напряжений при чистом изгибе плоского кривого бруса, так же как для прямого бруса, считаем справедливой гипотезу плоских сечений. Определяя деформации волокон бруса, пренебрегаем н

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ В КРИВОМ БРУСЕ ПРИ ЧИСТОМ ИЗГИБЕ
Для вычисления напряжений по формуле (14.6), полученной в предыдущем параграфе, необходимо знать, как проходит нейтральная ось. Для этой цели надо определить радиус кривизны нейтрального слоя г

НАПРЯЖЕНИЕ ПРИ ОДНОВРЕМЕННОМ ДЕЙСТВИИ ПРОДОЛЬНОЙ СИЛЫ И ИЗГИБАЮЩЕГО МОМЕНТА
Если в сечении кривого бруса одновременно возникают изгибающий момент и продольная сила, то напряжение следует определять как сумму напряжений от двух указанных воздействий:

Т F *? "л 99 R f Q ft " Ч

МЕТОД ЭЙЛЕРА ДЛЯ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКИХ СИЛ. ВЫВОД ФОРМУЛЫ ЭЙЛЕРА
Для исследования устойчивости равновесия упругих систем имеется несколько методов. Основы и техника применения этих методов изучаются в специальных курсах, посвященных проблемам устойчивости разли

СТЕРЖНЯ НА ВЕЛИЧИНУ КРИТИЧЕСКОЙ СИЛЫ
На рис. 358 показаны различные случаи закрепления концов сжатого стержня. Для каждой из этих зада*ч необходимо проводить свое решение аналогично тому, как это сделано в предыдущем параграфе для ша