рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Строительство
- /
- КОСОЙ ИЗГИБ
Реферат Курсовая Конспект
КОСОЙ ИЗГИБ
КОСОЙ ИЗГИБ - раздел Строительство, ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ Косым Изгибом Называется Такой Случай Изгиба Бруса, При Котором Плоско...
Косым изгибом называется такой случай изгиба бруса, при котором плоскость действия суммарного изгибающего момента в сечении не совпадает ни с одной из главных осей инерции. Короче говоря, в сечении возникают два изгибающих момента: Мх и Ми.
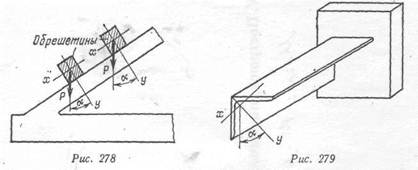
Так, например, обрешетины кровли (рис. 278) работают на косой изгиб. Вертикальная нагрузка от веса кровли и собственного веса обрешетин наклонена к главной оси под некоторым углом а.
Собственный вес уголка, заделанного одним концом в стену (рис. 279), также будет вызывать косой изгиб, так как главные оси
сечения уголка наклонены по отношению к нагрузке под некоторым углом.
Рассмотрим отдельно ряд наиболее важных вопросов, связанны с расчетом стержней на косой изгиб.
|
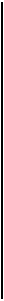
 1. Определение напряжений при косом из г и б е. Рассмотрим балку, заделанную одним концом, на которую действует сила Р, приложенная в центре тяжести концевого сечения
1. Определение напряжений при косом из г и б е. Рассмотрим балку, заделанную одним концом, на которую действует сила Р, приложенная в центре тяжести концевого сечения
|
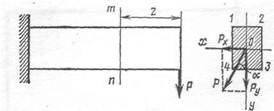
под углом а к оси Оу (рис. 280).
Разложим силу Р на две составляющие по осям
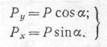
|
(11.1)
 Изгибающие моменты в сечении т-п относительно
Изгибающие моменты в сечении т-п относительно
главных осей инерции в соответствии с установленным правилом знаков определяются равенствами:
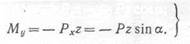
|
Мх = — Pyz = — Рг cos a;
(11.2)
Таким образом, в каждом сечении стержня одновременно действуют два изгибающих момента, которые создают изгиб в двух главных плоскостях.
Для определения напряжений от каждого момента в отдельности можно воспользоваться формулой, полученной ранее для плоского изгиба. Пользуясь принципом независимости действия сил, можно написать общую формулу напряжения в произвольной точке, лежащей в положительной четверти осей координат,
Д/f Д/f . *
 *х Jy V '
*х Jy V '
По формуле (11.3) можно определить напряжения в любой точке сечения. Подставляя в эту формулу координаты какой-либо точки
 с учетом их знаков, получим значение напряжения в этой точке. Для угловых точек модули координат у и х приобретают максимальные значения, поэтому формулу (11.3) можно представить в виде
с учетом их знаков, получим значение напряжения в этой точке. Для угловых точек модули координат у и х приобретают максимальные значения, поэтому формулу (11.3) можно представить в виде
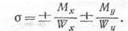
|
Здесь Wx и Wu — моменты сопротивления сечения.
|
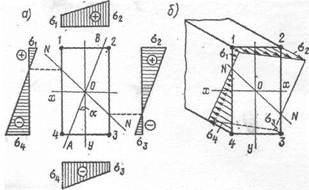
Рис. 281
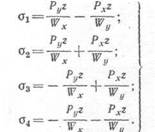
Для точек /, 2, 3 и 4 (рис. 281), учитывая при определении знаков физический смысл задачи, можно написать:
|
(ПА)
Наибольшее растягивающее напряжение будет в точке 2, наибольшее сжимающее — в точке 4.
Вычислив напряжения в четырех точках, можно построить эпюру напряжений. Существует два способа изображения эпюры при косом изгибе. Первый заключается в том, что строят эпюры по граням сечения, как это показано на рис. 281, а. Снеся на грани сечения нулевые точки эпюр напряжений, можно провести нейтральную линию, или, иначе, нулевую линию NN, в которой напряжения во всех точках равны нулю. След А В силовой плоскости пересекает нулевую линию NN под некоторым углом.
По второму способу строится пространственная эпюра напряжений, как показано на рис. 281, б. Вычислив наибольшие напряжения при косом изгибе, можно проверить прочность стержня, сравнивая полученное напряжение с расчетным сопротивлением.
Формулами (11.4) можно пользоваться только для тех точек, которые одновременно принадлежат волокнам, наиболее удаленным от главных осей инерции сечения. Для остальных точек эти формулы применять нельзя.
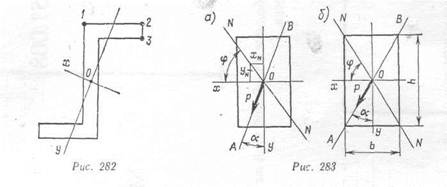
В целом ряде случаев поперечное сечение не имеет таких точек, которые одновременно наиболее удалены от обеих осей. Так, например, для сечения, показанного на рис. 282, точка 2 дальше других отстоит от оси Ох, а к оси Оу точка 2 ближе, чем точка 3.
Для отыскания наибольших напряжений з подобных сечениях пользуются формулой (11.3). В таких случаях вначале отыскивают точку, в которой напряжение максимально. Во многих случаях этазадача решается вычислением напряжений в ряде точек. Так, например, для сечения, показанного на рис. 282, достаточно вычислить напряжения в трех точках /, 2 и 3 и по ним установить максимум.
|
Для произвольного сечения необходимо вначале установить положение нулевой линии, а затем точку, которая дальше других отстоит от этой линии. Легко показать, что именно в этой точке напряжение максимально. В самом деле, равенство (11.3)представляет собой уравнение плоскости, проходящей через нулевую линию. Ордината, замеренная по нормали от поперечного сечения до этой плоскости, численно равна напряжению в данной точке. Она будет наибольшей для той точки, которая дальше всех отстоит от нулевой линии.
2. Определение положения нулевой линии в поперечном сечении бруса при косом изгибе. Положение нулевой линии при косом изгибе можно установить, если приравнять нулю напряжения в точках, принадлежащих этой линии. Пусть текущие координаты нулевой линии будут xN и уц, тогда, применяя формулу (11.3), получим
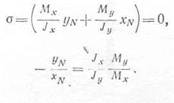
|
откуда находим
(11.5)
Пусть оси координат выбраны так, что моменты Му и Мх имеют одинаковые знаки, тогда правая часть равенства (11.5) будет положительной. В этом случае выражение (11.5) удовлетворяется тогда, когда знаки у координат xN и yN различны. Следовательно, нулевая линия не может проходить через первую четверть (рис. 283, а).
Обозначая угол наклона нулевой линии к осп Ох через ср и учитывая, что ум и Хдг имеют разные знаки, получим

|
Таким образом,
(11.6)
Если по формуле (11.6) получится отрицательный угол, то нулевую линию надо провести через положительную четверть осей координат.
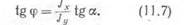
|
 Рассмотрим частный случай изгиба консоли силой Р, как показано на рис. 280. Подставляя в формулу (11.6) значения моментов из равенств (11.2) и сокращая на Рг, получим
Рассмотрим частный случай изгиба консоли силой Р, как показано на рис. 280. Подставляя в формулу (11.6) значения моментов из равенств (11.2) и сокращая на Рг, получим
Как видно из уравнения (11.7), нулевая линия не перпендикулярна силовой линии. Углымежду этими линиями тем больше отличаются друг от друга, чем больше разница между двумя главными моментами инерции. Только в тех сечениях, у которых моменты инерции относительно обеих осей равны друг другу (круглого, квадратного и др.), нулевая и силовая линии пересекаются под углом 90°.
В частном случае, когда для бруса с прямоугольным сечением силовая линия проходит по одной из диагоналей (рис. 283, б), применяя формулу (11.7), находим
{йФ = ШАь _ h
ёч" (lib3,12) Л b "
Таким образом, нулевая линия проходит по другой диагонали. Из этого примера наглядно видно, как отклоняются друг от друга указанные линии.
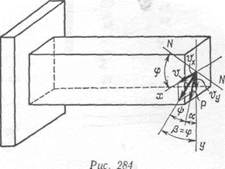
3. П р о г и б ы при косом изгибе. Разложив опять силу Р на две составляющие Р„ и Рх (рис. 284), найдемотдельно прогибы от этих составляющих. Обозначив прогибы конца консоли длиной / по направлению осей у и х через ру и vx, имеем:
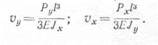
|
Суммарный прогиб можно найти как геометрическую сумму:
Найдем теперь направление суммарного перемещения. Для этого определим значение угла наклона этого перемещения к вертикали:
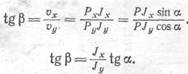
|
Таким образом,
Полученная формула идентична с формулой (11.7). Это позволяет сделать заключение, что Р = ср.
Следовательно, направление прогибов перпендикулярно нулевой линии. Вместе с тем отсюда вытекает важное условие, что направление прогибов не совпадает с направлением действующей силы. Это обстоятельство и послужило причиной того, что изгиб стали называть косым.
Если нагрузка представляет собой плоскую систему сил, то ось изогнутого бруса лежит в плоскости, которая не совпадает с плоскостью действия сил.
В случаях действия пространственной системы сил ось изогнутого стержня представляет собой пространственную кривую.
– Конец работы –
Эта тема принадлежит разделу:
ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ
На сайте allrefs.net читайте: ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПРИ ИЗГИБЕ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: КОСОЙ ИЗГИБ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов