рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Метод Гауса
Реферат Курсовая Конспект
Метод Гауса
Метод Гауса - раздел Философия, НАБЛИЖЕННЯ ЧИСЕЛ. ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ Теоретичні Відомості Найпростішим Методом Ро...
Теоретичні відомості
Найпростішим методом розв’язування систем лінійних алгебраїчних рівнянь є метод послідовного включення змінних, або метод Гауса. Є кілька модифікацій цього методу. Розглянемо схему єдиного ділення, за якою систему розв’язують в два етапи. На першому етапі вихідну систему рівнянь зводять до рівносильної їй системи трикутної форми. Цей процес перетворення називають зворотним ходом, знаходять розв’язок лінійної системи рівнянь трикутної форми.
Обмежимося розглядом системи трьох рівнянь з трьома змінними
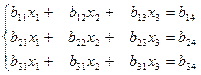

 (1)
(1)
визначник 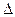 якої не дорівнює нулю.
якої не дорівнює нулю.
Нехай  ≠0. Поділимо коефіцієнти першого рівняння системи (1), включаючи й вільний член, на коефіцієнти
≠0. Поділимо коефіцієнти першого рівняння системи (1), включаючи й вільний член, на коефіцієнти  . Дістанемо нове рівняння
. Дістанемо нове рівняння
 (2)
(2)
де 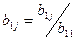 , (j=2,3,4). (3)
, (j=2,3,4). (3)
Включимо тепер змінну 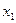 з другого боку і третього рівнянь системи (1). Для цього рівняння (3) помножимо послідовно спочатку на коефіцієнт
з другого боку і третього рівнянь системи (1). Для цього рівняння (3) помножимо послідовно спочатку на коефіцієнт  і віднімемо його від другого рівняння системи (1), а потім на
і віднімемо його від другого рівняння системи (1), а потім на 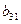 і віднімемо від третього рівняння системи (1). Дістанемо систему двох рівнянь з двома змінними
і віднімемо від третього рівняння системи (1). Дістанемо систему двох рівнянь з двома змінними 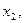
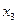 .
.
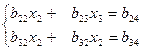 ( 4)
( 4)
де коефіцієнти 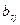 обчислюються за формулами
обчислюються за формулами
 (і=2,3; j=2,3,4). (5)
(і=2,3; j=2,3,4). (5)
Далі поділимо коефіцієнти першого рівняння системи (4) на 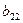 . Дістанемо рівняння
. Дістанемо рівняння
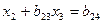 ( 6)
( 6)
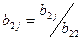 ,(j=3,4). (7)
,(j=3,4). (7)
Із системи (4) виключимо змінну 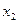 . Дістанемо рівняння
. Дістанемо рівняння
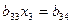 , (8)
, (8)
де
 , (j=3,4) ( 9)
, (j=3,4) ( 9)
З рівняння (8) маємо
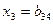 , (10)
, (10)
Після трьох кроків перетворення дістанемо систему рівнянь трикутної форми
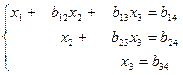 (11)
(11)
яка еквівалентна системі (1).
На цьому прямий хід методу Гауса завершено. Описаний процес перетворень системи (1) до рівносильної їй системи (11) можна здійснити, якщо виконуються умови 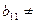 0,
0, 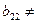 0,
0, 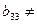 0.
0.
Оскільки системи (1) і (11) еквівалентні, то розв’язком системи (1) буде розв’язок системи (11), який можна записати так

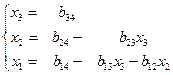 (12)
(12)
Цим завершено зворотній хід методу Гауса.
Приклад:Методом Гауса розв’язати систему рівнянь
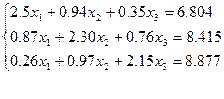 (13)
(13)
Коефіцієнти і вільні члени якої є точними числами.
Розв’язання: переконаємось спочатку, що система не вироджена і добре обумовлена. Для цього підрахуємо визначник системи: 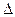 =9,035498. Значення визначника системи становить 361% значення найбільшого коефіцієнта системи
=9,035498. Значення визначника системи становить 361% значення найбільшого коефіцієнта системи 
За схемою єдиного ділення систему розв’язуємо в такий спосіб.
1. Коефіцієнти і вільні члени системи (13) записуємо у перші три рядки (стовпці 3-6) табл..1 Підраховуємо контрольні і рядкові суми, які збігаються між собою, і записуємо їх у 7-му і 8-му стовпцях.
Таблиця 1
| Крок перетворення | Рядок | Коефіцієнт при змінних 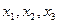
| Вільний член | Контроль | ||||
| Контрольна сума | Рядкова сума | |||||||
| 2,5 0,87 0,26 | 0,94 2,3 0,97 | 0,36 0,76 2,15 | 6,804 8,415 8,877 | 10,604 12,345 12,257 | 10,604 12,345 12,257 | |||
| 0,376 1,9729 0,8722 | 0,144 0,6347 2,1126 | 2,7216 6,0472 8,1694 | 4,2416 8,6548 11,1542 | 4,2416 8,6548 11,1542 | ||||
| 0,3217 1,8320 | 3,0651 5,4960 | 4,3868 7,3280 | 4,3868 7,3280 | |||||
| 3,0000 2,1000 1,5000 | 4,0000 3,1000 2,5000 | 4,0000 3,1000 2,5000 | ||||||
2. Усі числа першого рядка, крім рядкової суми, ділимо на  . Результати ділення записуємо в четвертий рядок. Усі проміжні обчислення виконуємо з двома запасними десятковими розрядами. Рядкова сума 1+0,376+0,144+2,7216=4,2416 збігається з контрольною сумою 10,604:2,50=4,2416, а це означає, що випадкових помилок немає.
. Результати ділення записуємо в четвертий рядок. Усі проміжні обчислення виконуємо з двома запасними десятковими розрядами. Рядкова сума 1+0,376+0,144+2,7216=4,2416 збігається з контрольною сумою 10,604:2,50=4,2416, а це означає, що випадкових помилок немає.
3. Обчислюємо коефіцієнти 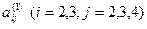 системи (4) за формулою (5) і записуємо
системи (4) за формулою (5) і записуємо
Їх у 5-ий і 6-ий рядки. Контрольні суми
12,345-0,87*4,2416=12,345-3,690=8,6548,
12,257-0,26*4,2416=12,257-1,103=11,1542
Збігаються з відповідними рядковими сумами
1,9729+0,6347+6,0472=8,6548,
0,8722+2,1126+8,1694=11,1542
А це означає, що обчислення виконано правильно.
4. Усі числа рядка 5, крім числа, що стоїть і 8-му стовпці, ділимо на 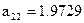 , і результати записуємо в 7-й рядок. Контрольна сума дорівнює 8,6548:1,9729=4,3868 , івона збігається з рядковою сумою
, і результати записуємо в 7-й рядок. Контрольна сума дорівнює 8,6548:1,9729=4,3868 , івона збігається з рядковою сумою
1+0,3217+3,0651=4,3868.
5. Коефіцієнт 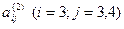 рівняння (8) обчислюємо за формулами (9) і записуємо в 8-й рядок. Контрольна сума 11,1542-4,3868*0,8722=7,3280 збігається з рядковою 1,8320+5,4960=7,3280.
рівняння (8) обчислюємо за формулами (9) і записуємо в 8-й рядок. Контрольна сума 11,1542-4,3868*0,8722=7,3280 збігається з рядковою 1,8320+5,4960=7,3280.
6.Зворотний хід виконуємо за формулами (12). При цьому використовуються 8-й, 7-й і 4-й рядки таблиці 1. з 8-го рядка дістаємо:
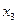 =5,4960:1,8320=3,0000;
=5,4960:1,8320=3,0000;
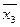 =7,3280:1,8320-4,0000.
=7,3280:1,8320-4,0000.
З 7-го рядка маємо:
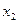 =3,0651-0,3217*3=2,1000
=3,0651-0,3217*3=2,1000
 =4,3868-0,3217*4=3,1000.
=4,3868-0,3217*4=3,1000.
Нарешті, з 4-го рядка знаходимо:
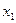 =2,7216-0,144*3-0,376*2,1=1,5000,
=2,7216-0,144*3-0,376*2,1=1,5000,
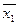 =4,2416-0,144*4-0,376*3,1=2,5000.
=4,2416-0,144*4-0,376*3,1=2,5000.
Обчисленні значення 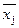 і
і 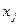 зв’язані між собою співвідношенням
зв’язані між собою співвідношенням 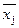 =
=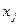 +1 (j=1,2,3),що свідчить про відсутність випадкових обчислювальних помилок.
+1 (j=1,2,3),що свідчить про відсутність випадкових обчислювальних помилок.
– Конец работы –
Эта тема принадлежит разделу:
НАБЛИЖЕННЯ ЧИСЕЛ. ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ
Розділ... НАБЛИЖЕННЯ ЧИСЕЛ... ЧИСЕЛЬНІ МЕТОДИ РОЗВ ЯЗУВАННЯ ЗАДАЧ ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Метод Гауса
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов