рефераты конспекты курсовые дипломные лекции шпоры

Раздел Философия
/
Метод скінчених різниць для граничної задачі, для лінійного диференціального рівняння другого порядку з змінними коефіцієнтами.

Реферат Курсовая Конспект

Выберите учебное заведение

Метод скінчених різниць для граничної задачі, для лінійного диференціального рівняння другого порядку з змінними коефіцієнтами.

Метод скінчених різниць для граничної задачі, для лінійного диференціального рівняння другого порядку з змінними коефіцієнтами. - раздел Философия, НАБЛИЖЕННЯ ЧИСЕЛ. ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ Нехай Задане Диференціальне Рівняння: ...

Нехай задане диференціальне рівняння:

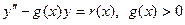(1)

і крайові умови: 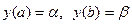(2) або

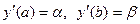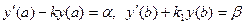(2‘)

(2)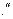

Потрібно знати розв‘язок диференціального рівняння у вигляді таблиці значень на .

Розіб‘ємо на частини точками:

, ,

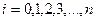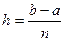
Другу похідну в рівнянні (1) замінимо різницевим відношенням:

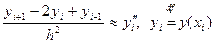
Тоді отримаємо систему:

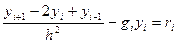
(3)

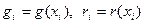
В залежності від крайових умов до системи (3) будуть додані рівняння:

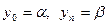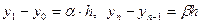(4)

(4‘)

Враховуючи формули чисельного диференціювання функцій інтерполювання многочленами Ньютона.

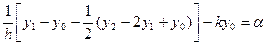
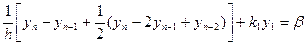або

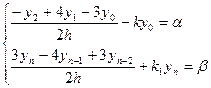(4‘‘)

Отримаємо систему 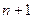рівнянь з 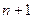невідомими. Дана система буде мати єдиний розв‘язок якщо відповідна однорідна система (випадок коли 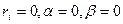) матиме лише тривіальний розв‘язок.

Введемо позначення:

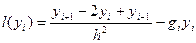
Лема1. Нехай дана довільна система з 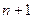точок: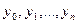

Якщо 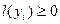, для довільного 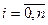, то найбільшим додатнім числом серед може бути 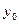або .

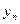Нехай 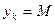- найбільше додатне число, .

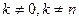Тоді існують числа 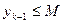, 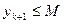. Маємо:

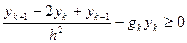, тоді випливає

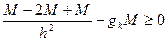, тобто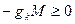

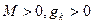, що неможливо.

Лема2. Якщо задана система точок 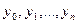і виконується умова 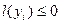, , 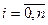то найменшим від‘ємним числом серед може бути лише 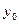або .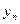

Доведення аналогічне.

Доведемо, що система (3) з крайовими умовами (4), (4‘), (4‘‘) має лише тривіальний розв‘язок у випадку коли .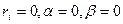

1. Нехай маємо (3) і умови (4). Якщо існує ненульовий розв‘язок, то серед чисел 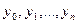є найбільше додатне або найменше від‘ємне, а це суперечить Лемі 1 або 2.

2. Нехай маємо (3) і умови (4‘), маємо: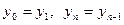

Якщо існує ненульовий розв‘язок, то серед чисел 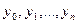є найбільше додатне або найменше від‘ємне. Знову суперечність з Лемою 1 або 2.

3. Система (3) і умови (4‘‘): 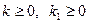і хоча б одне з них не дорівнює 0. Тоді в (3) підставимо :

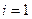Визначивши з (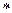) 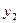і підставимо в ().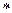

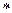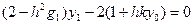
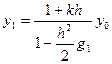(5)

Аналогічне підставивши 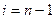в систему (3) маємо:

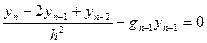
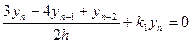
З останньої системи можна визначити:

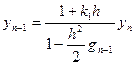(6)

Розглянемо рівності (5) і (6). Нехай знову існує деякий нетривіальний розв‘язок системи, тоді найбільше додатне або найменше від‘ємне число 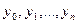можуть бути 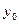або .

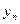Нехай 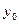- найбільше додатне число, тоді крок виберемо настільки малим щоб:

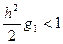, тоді з (5):

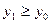, що неможливо з Лемою.

Щоб отримати таблицю розв‘язків диференціального рівняння при всіх розглянутих крайових умовах слід розв’язати одним з відомих способів систему (3) і (4) або (4‘) або (4‘‘).

Якщо позначити наближений а 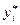- точний розв‘язки, тоді величина: 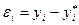вказує похибку в вузлі 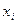. Можна довести, що похибка оцінюється таким співвідношенням:

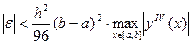(7)

Заваження1: Розглянутий метод можна застосувати також для рівнянь виду:

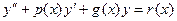(8)

з умовами:

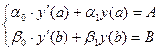(9)

Якщо другу похідну замінити так само як в попередніх випадках, а першу похідну так:

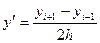, отримаємо:

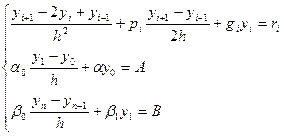(10)

Зауваження2: Похідні замінюють таким співвідношенням:

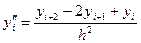
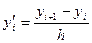
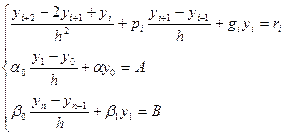(11)

В усіх розглянутих випадках похибка оцінюється нерівністю (7).

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

НАБЛИЖЕННЯ ЧИСЕЛ. ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ

Розділ... НАБЛИЖЕННЯ ЧИСЕЛ... ЧИСЕЛЬНІ МЕТОДИ РОЗВ ЯЗУВАННЯ ЗАДАЧ ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Метод скінчених різниць для граничної задачі, для лінійного диференціального рівняння другого порядку з змінними коефіцієнтами.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

АБСОЛЮТНА І ВІДНОСНА ПОХИБКИ. ПРИЧИНИ ВИНИКНЕННЯ ПОХИБОК
Неточність математичного опису задачі – неусувна похибка (неточність задання вхідних даних) та неповна відповідність математичній моделі. Метод який застосовується є

Доведення
Нехай дано точні числа х1,х2,...,хn та Х1,Х2,...,ХN. Розглянемо їх алгебраїчну суму:

Доведення
Нехай дано числа . ,

ЗАГАЛЬНА ПОХИБКА ДЛЯ ФОРМУЛИ
(Похибка функції) Нехай задана система величин . Задані похибки

ІТЕРАЦІЙНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ РІВНЯНЬ. ПРИНЦИП СТИСКУЮЧИХ ВІДОБРАЖЕНЬ В МЕТРИЧНОМУ ПРОСТОРІ.
Нехай дано рівняння (1). Суть полягає в наступному: нехай в деякій достатньо малій області Д існує єди

МЕТОД ПОДІЛУ ВІДРІЗКА ПОПОЛАМ
(МЕТОД ДИХОТОМІЇ) Нахай задане рівняння . Нехай

УТОЧНЕННЯ КОРЕНІВ РІВНЯННЯ МЕТОДОМ ХОРД
(МЕТОД ПРОПОРЦІЙНИХ ВІДРІЗКІВ) Нехай дано рівняння . Залишимо в силі припущення п

Доведення
Щоб скористатися принципом стискуючого відображення досить показати, що в деякому околі R кореня похідна функції

Доведення
Нехай- розв’язок рівняння, щоб використати принцип стискуючих відображень потрібно показати окіл точки

МЕТОД ПРОСТОЇ ІТЕРАЦІЇ ДЛЯ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ
Нехай (1), де неперервна на

Доведення
Розглянемо два послідовні наближення .

Метод Гауса
Теоретичні відомості Найпростішим методом розв’язування систем лінійних алгебраїчних рівнянь є метод послідовного включення змінних, або метод Гауса. Є кілька модиф

МЕТОД ПРОСТОЇ ІТЕРАЦІЇ РОЗВ’ЯЗУВАННЯ СИСТЕМИ ЛІНІЙНИХ, АЛГЕБРАЇЧНИХ РІВНЯНЬ
Нехай задано система рівнянь:(1) Або

ОЦІНКА ПОХИБКИ НАБЛИЖЕНЬ ПРОЦЕСУ ІТЕРАЦІЇ.
Шукають модуль різниці між попереднім і наступним і він має бути меншим за . Нехай задано два послідов

Етап: прямий хід.
Як відомо з алгебри симетричну матрицю можна представити у вигляді добутку двох транспонованих матриць: .

МЕТОДИ РОЗВ’ЯЗУВАННЯ НЕЛІНІЙНИХ СИСТЕМ
Нехай задана система рівнянь: (1) 1). МЕТОД НЬЮТОНА.

КОЕФІЦІЄНТИ ЛАГРАНЖА. ОЦІНКА ПОХИБКИ ІНТЕРПОЛЯЦІЇ.
Вираз (1) називається коефіцієнтами Лагранжа. Тоді многочлен Лагранжа набере вигляду:

CКІНЧЕННІ РІЗНИЦІ
Нехай задана функція . Позначимо

Доведення
З формули (1) . Вважаючи оператор як ум

МНОГОЧЛЕНАМИ НЬЮТОНА.
Нехай нескінченно-диференційовна на функція

ЗАДАЧА ЧИСЕЛЬНОГО ІНТЕГРУВАННЯ ФУНКЦІЇ. ФОРМУЛИ ПРЯМОКУТНИКІВ.
Якщо функція

КВАДРАТУРНІ ФОРМУЛИ НЬЮТОНА-КОТЕСА.
Нехай задана функція і задане розбиття відрізка

ФОРМУЛИ ТРАПЕЦІЇ.
В формули (1), (2) підставимо , тоді з формули (2) будемо мати:

КУСКОВО-КУБІЧНА СПЛАЙН ІНТЕРПОЛЯЦІЯ.
Означення: Сплайном називається функція для якої існує поділ її області визначення на підобласті, такі що в середині кожної підобласті ця функція є многочленом деякого степеня

Означення: Різницевим рівнянням називається рівняння відносно функції дискретної змінної.
Розглянемо найпростіший випадок одного лінійного рівняння відносно невідомої функції одного цілочисельного аргументу.

НАБЛИЖЕННЯ ФУНКЦІЙ В ЛІНІЙНОМУ НОРМОВАНОМУ ПРОСТОРІ. УМОВИ ІСНУВАННЯ ТА ЄДНОСТІ ЕЛЕМЕНТА НАЙКРАЩОГО НАБЛИЖЕННЯ.
Нехай - лінійний нормований простір,

N.1 НАБЛИЖЕННЯ АЛГЕБРАЇЧНИМИ МНОГОЧЛЕНАМИ.
Візьмемо метричний простір функцій сумовних з квадратом, тобто функцій для яких виконується умова

N. 2 ДИСКРЕТНЕ СЕРЕДНЬОКВАДРАТИЧНЕ НАБЛИЖЕННЯ.
Нехай функція задана своїми значеннями в точках

N.3 СЕРЕДНЬОКВАДРАТИЧНЕ НАБЛИЖЕННЯ ТРИГОНОМЕТРИЧНИМИ МНОГОЧЛЕНАМИ.
Розглянемо простір функцій сумовних з квадратом на відрізку . Елемент найкращого наближення будемо шукати серед:

Доведення
покажемо, що на існують – і + точки. Оскільки

Доведення Теореми
Будемо вважати, що [а,в]=[0,1], бо можна це завжди досягнути шляхом заміни змінної. Розглянемо многочлен Бернштейна:

Тригонометричні многочлени найкращого наближення.
Означення: Тригонометричний многочлен порядку n наз. вираз: Теорема: (ІІ Теорема Веєрштраса): Якщо

Найкращого наближення.
Теорема Веєрштраса вказує що найкраще наближення існує, але не дає практичного способу побудови. Ефективних способів точної побудови многочлена найкращого наближення до даної функції не іс

Метод Ейлера.
Дано диференціальне рівняння , (1)

Модифікації методу Ейлера.
п.1. Удосконалений метод Ейлера. Дано ,

Методи Рунге-Кутта.
Задано диференціальне рівняння: (1) і початкова умова:

Метод Адамса
Нехай задано диференціальне рівняння: (1) Задана система точок:

Метод прогонки розв’язування крайових задач для звичайних диференціальних рівнянь другого порядку.
Нехай задане диференціальне рівняння: (1)